人教版七年级下学期数学7.1 平面直角坐标系 练习 含答案
文档属性
| 名称 | 人教版七年级下学期数学7.1 平面直角坐标系 练习 含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 64.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 00:00:00 | ||
图片预览



文档简介
7.1 平面直角坐标系
一.选择题(共8小题)
1.在平面直角坐标系中,下列各点位于x轴上的是( )
A.(1,﹣2) B.(3,0) C.(﹣1,3) D.(0,﹣4)
2.在平面直角坐标系的第二象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是( )
A.(3,﹣4) B.(4,﹣3) C.(﹣4,3) D.(﹣3,4)
3.点P的坐标为(2﹣a,3a+6),且到两坐标轴的距离相等,则点P的坐标为( )
A.(3,3) B.(3,﹣3)
C.(6,﹣6) D.(3,3)或(6,﹣6)
4.若点P(a,b)在第二象限,则点Q(b+5,1﹣a)所在象限应该是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知点P(0,m)在y轴的负半轴上,则点M(﹣m,﹣m+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知点P(1﹣2m,m﹣1),则不论m取什么值,该P点必不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.下列说法正确的是( )
A.点P(3,﹣5)到x轴的距离为﹣5
B.在平面直角坐标系内,(﹣1,2)和(2,﹣1)表示同一个点
C.若x=0,则点P(x,y)在x轴上
D.在平面直角坐标系中,有且只有一个点既在x轴上,又在y轴上
8.若|m|=2,|n|=3,则点A(m,n)( )
A.四个象限均有可能
B.在第一象限或第三象限或第四象限
C.在第一象限或第二象限
D.在第二象限或第三象限或第四象限
二.填空题(共5小题)
9.点P到x轴的距离是2,到y轴的距离是3,且在y轴的左侧,则P点的坐标是 .
10.在平面直角坐标系中,将点(﹣b,﹣a)称为点(a,b)的“关联点”(例如点(﹣2,﹣1)是点(1,2)的“关联点”).如果一个点和它的“关联点”在同一象限内,那么这一点在第 象限.
11.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),第4次接着运动到点(4,0),…,按这样的运动规律,经过第2019次运动后,动点P的横坐标是 .
12.若点P(2﹣a,2a+3)到两坐标轴的距离相等.则点P的坐标是 .
13.已知在平面直角坐标系中,点P在第二象限,且到x轴的距离为2,到y轴的距离为3,则点P的坐标为 .
三.解答题(共5小题)
14.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴;
(4)点P到x轴、y轴的距离相等.
15.在平面直角坐标系中,已知点M(m,2m+3).
(1)若点M在x轴上,求m的值;
(2)若点M在第二象限内,求m的取值范围;
(3)若点M在第一、三象限的角平分线上,求m的值.
16.在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“识别距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1(x1,y1)与点P2(x2,y2)的“识别距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则P1(x1,y1)与点P2(x2,y2)的“识别距离”为|y1﹣y2|;
(1)已知点A(﹣1,0),B为y轴上的动点,
①若点A与B的“识别距离为”2,写出满足条件的B点的坐标 .
②直接写出点A与点B的“识别距离”的最小值 .
(2)已知C点坐标为C(m,m+3),D(0,1),求点C与D的“识别距离”的最小值及相应的C点坐标.
17.对于a、b定义两种新运算“*”和“⊕”:a*b=a+kb,a⊕b=ka+b(其中k为常数,且k≠0).若平面直角坐标系xOy中的点P(a,b),有点P的坐标为(a*b,a⊕b)与之相对应,则称点P为点P的“k衍生点”
例如:P(1,4)的“2衍生点”为P′(l+2×4,2×1+4),即P′(9,6).
(1)点P(﹣1,6)的“2衍生点”P′的坐标为 .
(2)若点P的“3衍生点”P′的坐标为(5,7),求点P的坐标.
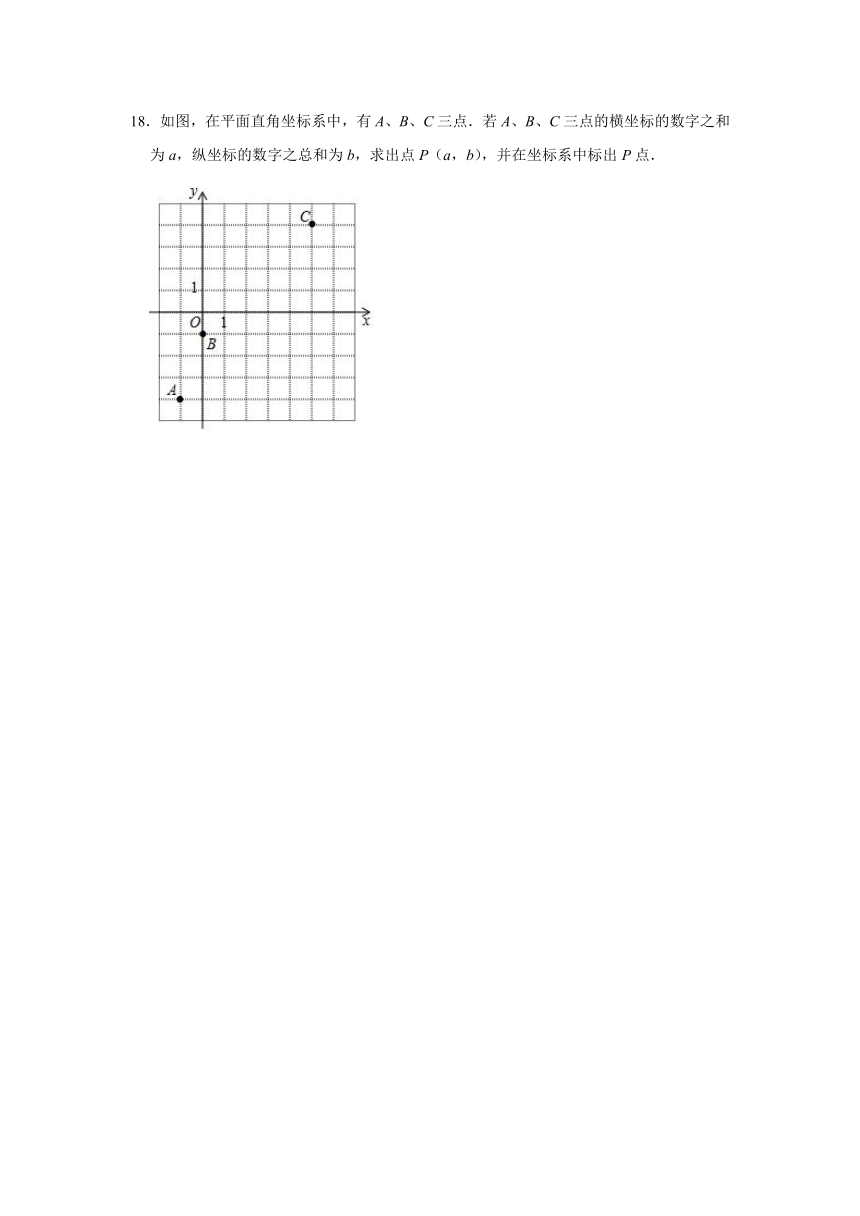
18.如图,在平面直角坐标系中,有A、B、C三点.若A、B、C三点的横坐标的数字之和为a,纵坐标的数字之总和为b,求出点P(a,b),并在坐标系中标出P点.
参考答案
一.选择题(共8小题)
1.
B.
2.
C.
3.
D.
4.
A.
5.
A.
6.
A.
7.
D.
8.
A.
二.填空题(共5小题)
9.
(﹣3,2)或(﹣3,﹣2).
10.
二、四.
11.
(2019,2)
12.
(7,﹣7)或(,).
13.
(﹣3,2).
三.解答题(共5小题)
14.解:(1)∵点P(a﹣2,2a+8),在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2))∵点P(a﹣2,2a+8),在y轴上,
∴a﹣2=0,
解得:a=2,
故2a+8=2×2+8=12,
则P(0,12);
(3)∵点Q的坐标为(1,5),直线PQ∥y轴;,
∴a﹣2=1,
解得:a=3,
故2a+8=14,
则P(1,14);
(4)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10则:a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2则:a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12),(﹣4,4).
15.解:(1)∵点M在x轴上,
∴2m+3=0
解得:m=﹣1.5;
(2)∵点M在第二象限内,
∴,
解得:﹣1.5<m<0;
(3)∵点M在第一、三象限的角平分线上,
∴m=2m+3,
解得:m=﹣3.
16.解:①(0,2)或(0,﹣2);
②“识别距离”的最小值是1;
故答案为:(1)(0,2)或(0,﹣2),1.
(2)|m﹣0|=|m+3﹣1|,
解得m=8或﹣,
当m=8时,“识别距离”为8
当m=﹣时,“识别距离”为,
所以,当m=﹣时,“识别距离”最小值为,相应C(﹣,).
17.解:(1)由题意可得,点P(﹣1,6)的“2衍生点”P′的坐标为:[﹣1+2×6,2×(﹣1)+6],即(11,4);
故答案为:(11,4);
(2)设点P的坐标为:(a,b),由题意可得:
,
解得:,
∴点P的坐标为:(2,1).
18.解:由图知,A、B、C三点的坐标分别为:
A(﹣1,﹣4),B(0,﹣1),C(5,4),
则a=﹣1+0+5=4,b=﹣4﹣1+4=﹣1,
故P的坐标为(4,﹣1),如图所示.
