人教版八年级上册13.3.2 等边三角形练习(无答案)
文档属性
| 名称 | 人教版八年级上册13.3.2 等边三角形练习(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 484.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 10:37:12 | ||
图片预览




文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 T等边三角形
授课日期及时段
教学内容
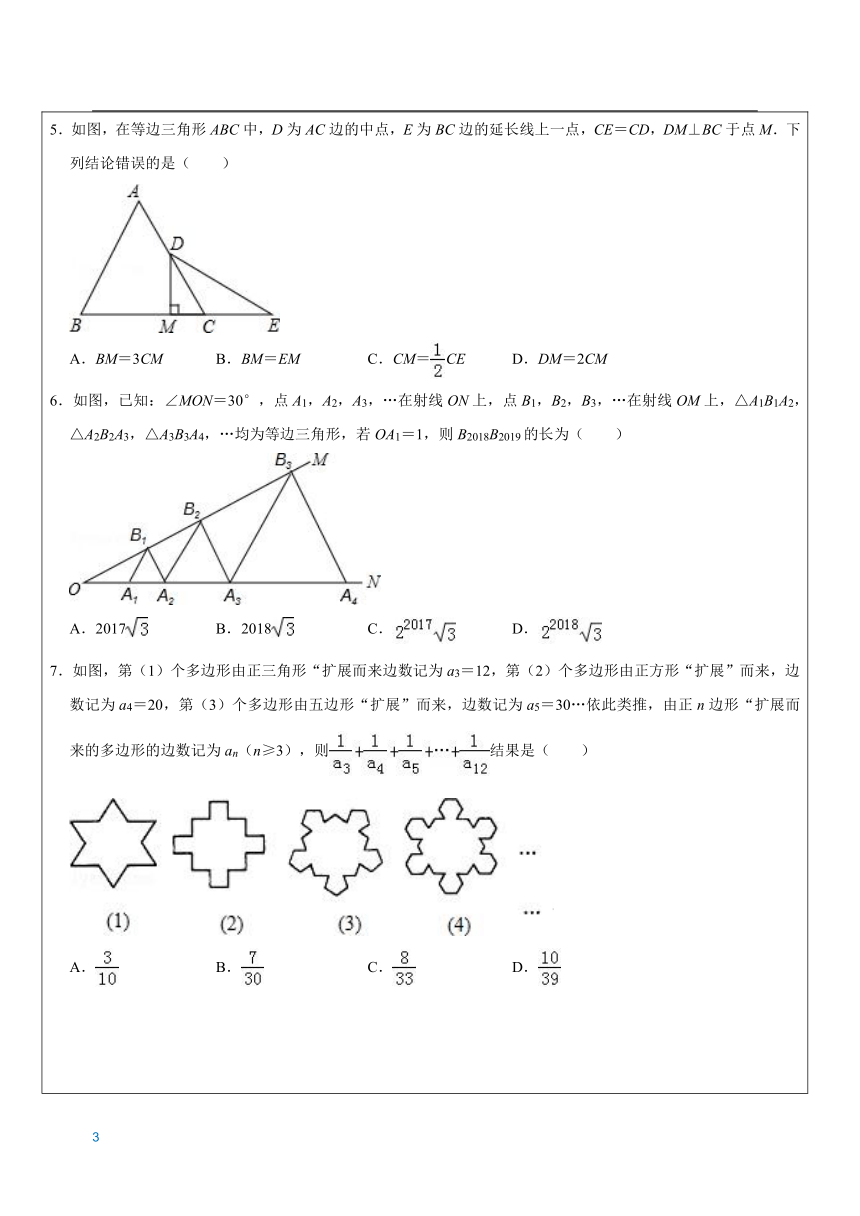
一、同步知识梳理 知识点1:等边三角形定义:三条边都相等的三角形叫做等边三角形 知识点2:等边三角形的性质: (1)等边三角形是锐角三角形,等边三角形的内角都相等,且均为60°。 (2)等边三角形每条边上的中线、高线和所对角的平分线互相重合(三线合一) (3)等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线 或对角的平分线所在的直线。 (4)等边三角形重心、内心、外心、垂心重合于一点,称为等边三角形的中心。(四心合一)⑹等边三角形内任意一点到三边的距离之和为定值(等于其高) 知识点3:等边三角形的判定: (1)三边相等的三角形是等边三角形(定义) (2)三个内角都相等(为60度)的三角形是等边三角形 (3)有一个角是60度的等腰三角形是等边三角形 (4)两个内角为60度的三角形是等边三角形 说明:可首先考虑判断三角形是等腰三角形。 等边三角形的性质与判定理解: 首先,明确等边三角形定义。三边相等的三角形叫做等边三角形,也称正三角形。其次,明确等边三角形与等腰三角形的关系。等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形。 知识点4:30°角的直角三角形 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,反之也成立. 二、同步题型分析 1、等边三角形三边 ,三个角都等于 , 2、等边三角形是轴对称图形,它有 条对称轴,它的对称轴 。er 题型1:性质 1.如图,等边三角形ABC的周长为18,则BC边上的高AD的长为( ) A.3 B.3 C.6 D.6 2.图1的直角柱由2个正三角形底面和3个矩形侧面组成,其中正三角形面积为a,矩形面积为b.若将4个图1的直角柱紧密堆叠成图2的直角柱,则图2中直角柱的表面积为何?( ) A.4a+2b B.4a+4b C.8a+6b D.8a+12b 3.如图,直线l1∥l2,将等边三角形如图放置若∠α=25°,则∠β等于( ) A.35° B.30° C.25° D.20° 4.如图,直线a∥b,等边三角形ABC的顶点B在直线b上,若∠1=34°,则∠2等于( ) A.84° B.86° C.94° D.96° 5.如图,在等边三角形ABC中,D为AC边的中点,E为BC边的延长线上一点,CE=CD,DM⊥BC于点M.下列结论错误的是( ) A.BM=3CM B.BM=EM C.CM=CE D.DM=2CM 6.如图,已知:∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=1,则B2018B2019的长为( ) A.2017 B.2018 C. D. 7.如图,第(1)个多边形由正三角形“扩展而来边数记为a3=12,第(2)个多边形由正方形“扩展”而来,边数记为a4=20,第(3)个多边形由五边形“扩展”而来,边数记为a5=30…依此类推,由正n边形“扩展而来的多边形的边数记为an(n≥3),则结果是( ) A. B. C. D. 8.如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.随x,m,n的值而定 9.如图.阴影部分是边长为1的小正三角形,A,B,C,D,E,F,G,H分别是8个正三角形,则A和B的边长分别是( ) A.2,4 B.2.5,5 C.3,6 D.4,8 10.如图,等边△ABC的边长为5,点D,P,L分别在边AB,BC,CA上,AD=BP=CL=x(x>0).按如图方式作边长均为3的等边△DEF,△PQR,△LMN,点F,R,N分别在射线DA,PB,LC上. ①当边DE,PQ,LM与△ABC的三边围成的图形是正六边形时,x= ; ②当点D与点B重合时,EF,QR,MN所围成的三角形的周长为 . 11.如图,在边长为6的等边△ABC中,E为BC边上一点,且BE=2,过E作EF⊥AC于F点,G为EF中点,D为AB边上一动点,连接DG,当D运动到AB边的三等分点时,则DG的长为 . 12.如图,在一个房间内,有一个梯子斜靠在墙上,此时梯子的倾斜角为75°.梯子顶端距地面的垂直距离MA为5米,如果梯子底端不动,顶端靠在对面墙上,此时梯子的倾斜角为45°.则这间房子的宽AB是 米. 13.在边长为4的等边三角形ABC中,P是BC边上的一个动点,过点P分别作PM⊥AB于M,PN⊥AC于N,连接PA,则下列说法正确的是 (填序号). ①若PB=1,则;②若PB=2,则S△ABC=8S△BMP; ③;④若0<PB≤1,则S四边形AMPN最大值是. 14.如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形.若OA1=a,则三角形AnBnAn+1的边长为 . 15.如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2010次,点P依次落在点P1,P2,P3,…,P2010的位置,则点P2010的坐标为 . 21*cnjy*com 题型2:判定 1.下列条件中,不能得到等边三角形的是( ) A.有两个内角是60°的三角形 B.三边都相等的三角形 C.有一个角是60°的等腰三角形 D.有两个外角相等的等腰三角形 2.如图,在钝角三角形ABC中,∠ABC为钝角,以点B为圆心,AB长为半径面弧;再以点C为圆心,AC长为半径画弧;两弧交于点D,连结AD,CB的延长线交AD于点E.下列结论错误的是( ) A.CE垂直平分AD B.CE平分∠ACD C.△ABD是等腰三角形 D.△ACD是等边三角形 3.下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( ) A.①②③④ B.①②④ C.①③ D.②③④ 4.若△ABC三个内角的度数分别为m、n、p,且|m﹣n|+(n﹣p)2=0,则这个三角形为( ) A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形 5.如图,∠AOB=120°,OP平分∠AOB,且OP=10.若点M,N分别在射线OA,OB上,且△PMN是边长为整数的等边三角形,则满足上述条件的点M有(参考数据:)( ) A.4个以上 B.4个 C.3个 D.2个 6.等腰△ABC的底角若为顶角的,过底边上的一点D作底边BC的垂线交AC于点E,交BA的延长线于点F,则△AEF是( ) A.等边三角形 B.直角三角形 C.钝角三角形 D.等腰但非等边三角形 7.如图,E是等边△ABC中AC边上的点,∠1=∠2,BE=CD,则△ADE的形状是( ) A.等腰三角形 B.等边三角形 C.不等边三角形 D.不能确定形状 8.如图,在四边形OAPB中,∠AOB=120°,OP平分∠AOB,且OP=2,若点M、N分别在直线OA、OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( ) A.1个 B.2个 C.3个 D.3个以上 9.如图,△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是( ) A.8+2a B.8+a C.6+a D.6+2a 10.如图,使中间部分形成一个小的等边△DEF.若△DEF的面积是△ABC的,则的值为 . 11.一只电子青蛙在如图的平面直角坐标系做如下运动:从坐标原点开始起跳记为A1,然后沿着边长为1的等边三角形跳跃即A1→A2→A3→A4→A5……已知A3的坐标为(1,0),则A2018的坐标是 . 12.下列三角形:(1)有两个角等于60°;(2)有一个角等于60°的等腰三角形;(3)三个外角都相等的三角形;(4)一腰上的中线也是这条腰上的高的等腰三角形,其中是等边三角形的有 . 13.如图,P是正六边形ABCDEF的BC边上的一点,过点P作PM∥AB交AF于M,AD于S,作PN∥CD交DE于N,AD于T,点O是AD的中点,OG平分∠MON,则图中等边三角形有 个. 题型3:证明等边三角形 1.已知∠AOB=30°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1,O,P2三点所构成的三角形是( ) A. 直角三角形 B. 钝角三角形 C. 等腰三角形 D. 等边三角形 2.下列说法:①有一个角是60°的等腰三角形是等边三角形;②如果三角形的一个外角平分线平行三角形的一边,那么这个三角形是等腰三角形;③三角形三边的垂直平分线的交点与三角形三个顶点的距离相等;④有两个角相等的等腰三角形是等边三角形.其中正确的个数有( ) A.1个 B.2个 C.3个 D.4个 3.如图,点P,M,N分别在等边△ABC的各边上,且MP⊥AB于点P,MN⊥BC于点M,PN⊥AC于点N. (1)求证:△PMN是等边三角形; (2)若AB=12cm,求CM的长. 4.如图,△ADE是等边三角形,DE∥BC,分别交AB、AC于点D、E.求证:△ABC是等边三角形. 5.如图,在等边△ABC中,点D,E分别在边BC、AC上,若CD=3,过点D作DE∥AB,过点E作EF⊥DE,交BC的延长线于点F. (1)求证:△CDE为等边三角形; (2)求EF的长. 6.如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动. (1)点M、N运动几秒后,M、N两点重合? (2)点M、N运动几秒后,可得到等边三角形△AMN? (3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间. 题型4:构造等边三角形 1.如图.四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120° 求证:AC=BC+DC. 2.如图,△ABC是等边三角形,点D是边BC上(除B、C外)的任意一点,∠ADE=60°,且DE交△ABC外角∠ACF的平分线CE于点E (1)求证:∠1=∠2; (2)求证:AD=DE. 3.如图:△ABD是等边三角形,以BD为边向外作等边三角形△DBC,点E,F分别在AB,AD上且AE=DF.连接BF于DE相交于点G,连接CG,证明下列结论: ①△AED≌△DFB; ②CG=DG+BG. 题型5:含30°角的直角三角形 1.如图,在Rt△ABC中,∠B=90°,∠ACB=60°,DE是斜边AC的垂直平分线,分别交AB、AC于D、E两点,若BD=2,则AC的长是( ) A.4 B.4 C.8 D.8 2.如图,△ABC是等腰三角形(AB=AC,∠B=30°),AD是底边BC上的高.BC=12米,则AD的长是( ) A.2米 B.2米 C.6米 D.4米 3.在Rt△ABC中,∠C=90°,CD是斜边边上的高,∠A=30°,那么下列说法中正确的是( ) A.AD=2BD B.AD=BD C.AD=3BD D.AD=4BD 4.如图,已知Rt△ABC中,∠C=90°,∠A=30°,AB=4,点D、E分别在边AC、AB上,若AD=DC,AE=CB+BE,则线段DE的长为( ) A.2 B. C. D.2 5.如图,在△ABC中,AB=AC,∠B=30°,AD⊥AB,交BC于点D,AD=4,则BC的长为( ) A.8 B.4 C.12 D.6 6.如图,在△ABC中,∠C=30°,点D在BC上,AE平分∠BAD,∠ADB=∠B+90°,下列结论正确的是( ) EC=2AE B.AC=2AE C.EC=AE D.AC=AE 7.如图,在△ABC中,AB=AC,∠BAC=30°,点D是AC上一点,∠ABD=15°.若BC=6,则 AD的长为 . 8.如图,△ABC中,AB=AC,∠A=30°,点D在边AB上,∠ACD=15°,则= . 9.如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为 . 10.图1所示的是某超市入口的双翼闸门,如图2,当它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°,求当双翼收起时,可以通过闸机的物体的最大宽度.
11.已知:如图示,在Rt△ABC中,∠A=90°,∠ABC=2∠C,BD是∠ABC的平分线.求证:CD=2AD. 12.如图,在Rt△ABC中,∠A=30°,∠ACB=90°,点D为AC中点,点E为AB边上一动点,AE=DE,延长ED交BC的延长线于点F.
(1)求证:△BEF是等边三角形;
(2)若AB=12,求DE的长. 13.如图,在平行四边形ABCD中,AE是BC边上的高,点F是DE的中点,AB与AG关于AE对称,AE与AF关于AG对称.
(1)求证:△AEF是等边三角形;
(2)若AB=2,求△AFD的面积. 14.一张展开后桌面平行于地面的折叠型方桌如图甲,从正面看如图乙,已知AO=BO=40cm,CO=DO=30cm,现将桌子放平,两条桌腿叉开的角度∠AOB刚好为120°,求桌面到地面的距离是多少?
15.如图,在△ABC中,BA=BC,∠B=120°,线段AB的垂直平分线MN交AC于点D,且AD=8cm.求:
(1)∠ADG的度数;
(2)线段DC的长度. 三、课堂达标检测 1.P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D. (1)证明:PD=DQ.(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长. 2.已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q. (1)求证:BE=AD; (2)求∠BPQ的度数; (3)若PQ=3,PE=1,求AD的长. 3.如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=4,PE=1. (1)求证:∠BPQ=60°; (2)求AD的长. 4.如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°, 连接CE. (1)求证:△ABD≌△ACE; (2)求证:CE平分∠ACF; (3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长. 5.如图,在△ABC中,CD是AB边上的高,BE是AC边上的中线,且BD=CE.求证: (1)点D在BE的垂直平分线上; (2)∠BEC=3∠ABE. 6.如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD 交于点D,连接CD. (1)求证:①AB=AD;②CD平分∠ACE. (2)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明. 7.如图,在△ABC中,∠ABC的角平分线OB与∠ACB的角平分线OC相交于点O,过点O作MN BC,分别交AB、AC于点M、N. (1)请写出图中所有的等腰三角形,并给予证明; (2)若AB+AC=14,求△AMN的周长. 8.如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN 是等边三角形: (1)当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由; (2)当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是, 请说明理由(可用第一问结论). 9.如图△ABC是等边三角形 (1)如图①,DE∥BC,分别交AB、AC于点D、E.求证:△ADE是等边三角形; (2)如图②,△ADE仍是等边三角形,点B在ED的延长线上,连接CE,判断∠BEC的度数及线 段AE、BE、CE之间的数量关系,并说明理由. 10.如图,△ABC中,AB=AC,AD、CE是高,连接DE. (1)求证:BC=2DE; (2)若∠BAC=50°,求∠ADE的度数. 11.如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过A点作BC的平行线交BE的 延长线于点F,连接CF. (1)求证:AF=DC; (2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论; (3)在(2)的条件下,若AB=8,BC=10,且AG⊥CF于G,求AG的长. 12.如图,在△ABC中,∠ACB=Rt∠,BC=6,AC=8,点D是AC的中点,点P为AB边上的动点(P不与A重合),AP=t(t>0),PH⊥AC于点H,则PH=t,连结DP并延长至点E,使得PE=PD,作点E关于AB的对称点F,连结FH
(1)用t的代数式表示DH的长;
(2)求证:DF∥AB;
(3)若△DFH为等腰三角形,求t(0<t≤5)的值.(提示:以∠A为较小锐角的直角三角形的三边比为3:4:5)
21
