人教版八年级上册13.4课题学习 最短路径问题学案(无答案)
文档属性
| 名称 | 人教版八年级上册13.4课题学习 最短路径问题学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 319.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-10 00:00:00 | ||
图片预览


文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 C (最短路径问题) C轴对称综合应用
授课日期及时段
教学内容
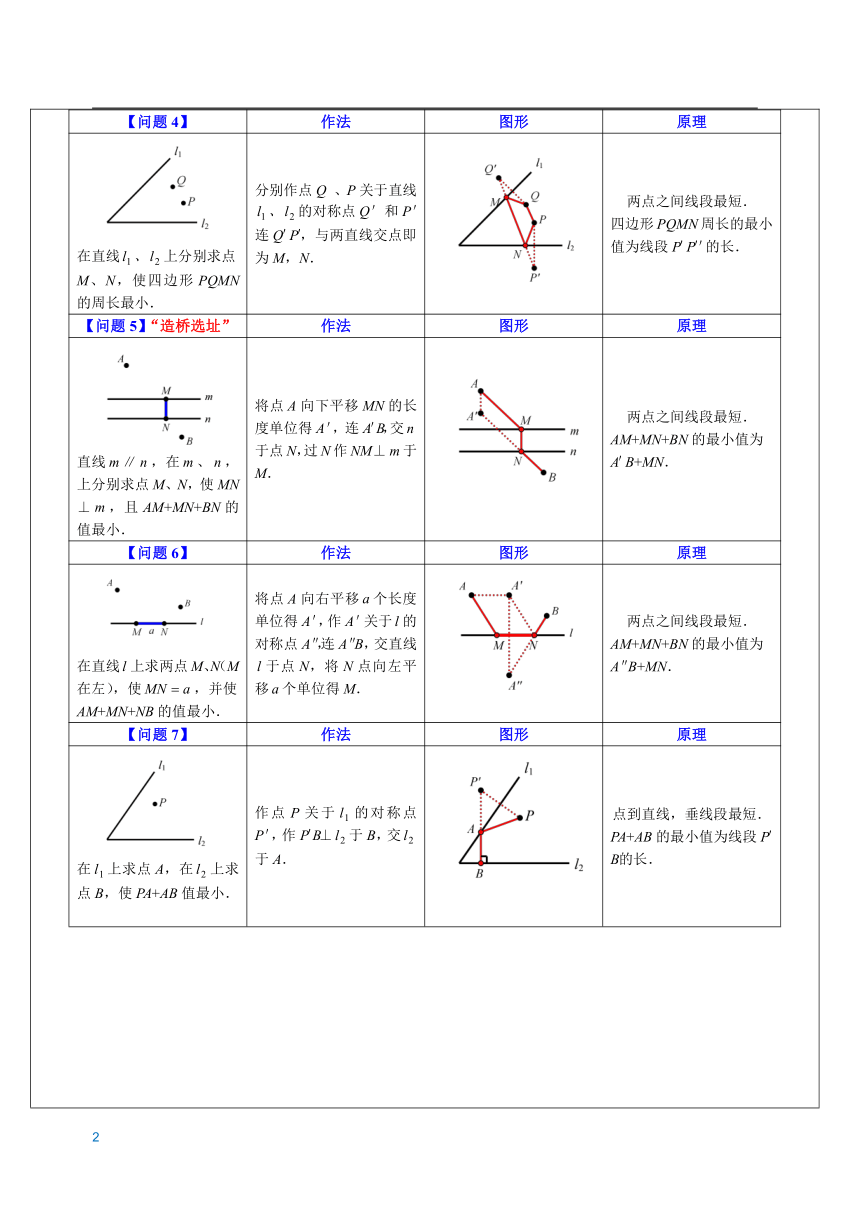
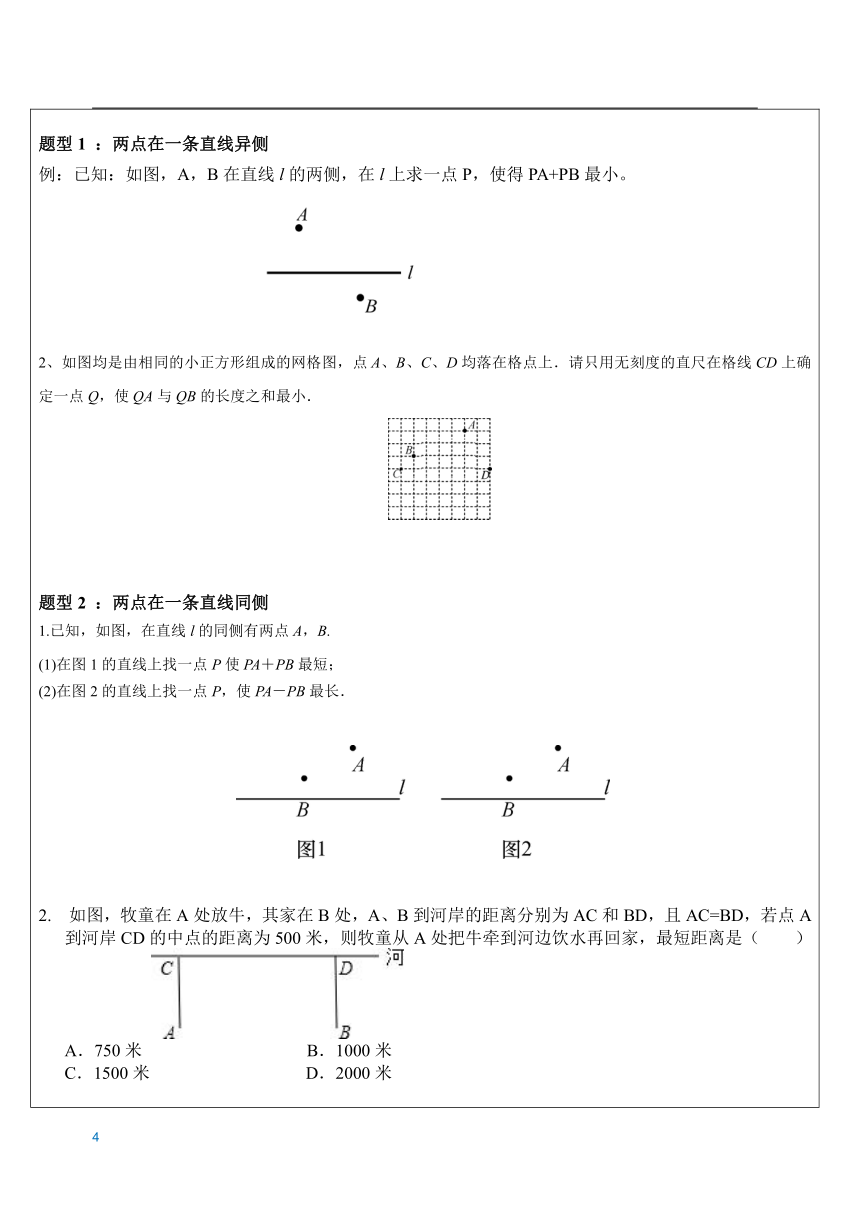
【问题1】 作法 图形 原理 在直线l上求一点P,使PA+PB值最小. 连AB,与l交点即为P.两点之间线段最短.PA+PB最小值为AB. 【问题2】“将军饮马” 作法 图形 原理 在直线l上求一点P,使PA+PB值最小. 作B关于l的对称点B'连A B',与l交点即为P.两点之间线段最短.PA+PB最小值为A B'. 【问题3】作法图形原理 在直线、上分别求点M、N,使△PMN的周长最小. 分别作点P关于两直线的对称点P'和P'',连P'P'',与两直线交点即为M,N.两点之间线段最短.PM+MN+PN的最小值为 线段P'P''的长. 【问题4】 作法 图形 原理 在直线、上分别求点M、N,使四边形PQMN的周长最小. 分别作点Q 、P关于直线、的对称点Q'和P'连Q'P',与两直线交点即为M,N.两点之间线段最短. 四边形PQMN周长的最小值为线段P'P''的长. 【问题5】“造桥选址” 作法 图形 原理 直线∥,在、,上分别求点M、N,使MN⊥,且AM+MN+BN的值最小. 将点A向下平移MN的长度单位得A',连A'B,交于点N,过N作NM⊥于M.两点之间线段最短.AM+MN+BN的最小值为A'B+MN. 【问题6】 作法 图形 原理 在直线上求两点M、N(M在左),使,并使AM+MN+NB的值最小. 将点A向右平移个长度单位得A',作A'关于的对称点A'', 连A''B,交直线于点N,将N点向左平移个单位得M.两点之间线段最短.AM+MN+BN的最小值为A''B+MN. 【问题7】 作法 图形 原理 在上求点A,在上求点B,使PA+AB值最小. 作点P关于的对称点P',作P'B⊥于B,交于A.点到直线,垂线段最短.PA+AB的最小值为线段P'B的长. 【问题8】 作法 图形 原理 A为上一定点,B为上一定点,在上求点M,在上求点N,使AM+MN+NB的值最小. 作点A关于的对称点A',作点B关于的对称点B',连A'B'交于M,交于N.两点之间线段最短.AM+MN+NB的最小值为线段A'B'的长. 【问题9】 作法 图形 原理 在直线l上求一点P,使的值最小. 连AB,作AB的中垂线与直线l的交点即为P.垂直平分上的点到线段两端点的距离相等.=0. 【问题10】作法图形原理 在直线l上求一点P,使的值最大. 作直线AB,与直线l的交点即为P.三角形任意两边之差小于第三边.≤AB.的最大值=AB. 【问题11】作法图形原理 在直线l上求一点P,使的值最大. 作B关于l的对称点B'作直线A B',与l交点即为P.三角形任意两边之差小于第三边.≤AB'.最大值=AB'. 【问题12】“费马点”作法图形原理 △ABC中每一内角都小于120°,在△ABC内求一点P,使PA+PB+PC值最小. 所求点为“费马点”,即满足∠APB=∠BPC=∠APC=120°.以AB、AC为边向外作等边△ABD、△ACE,连CD、BE相交于P,点P即为所求.两点之间线段最短.PA+PB+PC最小值=CD. 题型1 :两点在一条直线异侧例:已知:如图,A,B在直线l的两侧,在l上求一点P,使得PA+PB最小。 2、如图均是由相同的小正方形组成的网格图,点A、B、C、D均落在格点上.请只用无刻度的直尺在格线CD上确定一点Q,使QA与QB的长度之和最小. 题型2 :两点在一条直线同侧1.已知,如图,在直线l的同侧有两点A,B.(1)在图1的直线上找一点P使PA+PB最短; (2)在图2的直线上找一点P,使PA-PB最长. 2. 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是( )
A.750米 B.1000米 C.1500米 D.2000米 3、如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为( ). A.15° B.22.5° C.30° D.45° 4、如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( ). 3 B. 4 C. 5 D. 6 5、如图,在△ABC中,AB=AC,AD平分∠CAB,N点是AB上的一定点,M是AD上一动点,要使MB+MN最小,请找点M的位置. 题型3:一点在两相交直线内部1、如图,在△ABC的一边AB上有一点P. (1)能否在另外两边AC和BC上各找一点M、N,使得△PMN的周长最短?若能,请画出点M、N的位置,若不能,请说明理由; (2)若∠ACB=52°,在(1)的条件下,求出∠MPN的度数. 2、如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△周长最小,求∠AMN+∠ANM的度数. 3、如图,∠AOB=30°,内有一点P且OP=,若M、N为边OA、OB上两动点,那么△PMN的周长最小为( ). ?A. B. 6 C. D. 4、已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于2,则α=( ). A. 30° B. 45° C. 60° D. 90° 题型4:两点在两相交直线内部1、已知:如图,在∠POQ内部有两点M、N,∠MOP=∠NOQ. (1)画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上取一点B,使点B到点M和点N的距离和最小; (2)直接写出AM+AN与BM+BN的大小关系. 2、在某一地方,有条小河和草地,一天某牧民的计划是从A处的牧场牵着一只马到草地牧马,再到小河饮马,你能为他设计一条最短的路线吗?(在N上任意一点即可牧马,M上任意一点即可饮马.)(保留作图痕迹,需要证明) 题型5:造桥选址问题1、如图,村庄A,B位于一条小河的两侧,若河岸a,b彼此平行,现在要建设一座与河岸垂直的桥CD,问桥址应如何选择,才能使A村到B村的路程最近? 2、在P、Q两村之间有两条河,且每条河的宽度相同,从P村到Q村,要经过两座桥MN、EF。现在要设计一条道路,并在两条河上分别架这两座垂直于桥的大桥,问:如何设计这两座桥MN,EF的位置,使由P村到Q村的路程最短?
C专题——最短路径
1
