人教版八年级上册 14.2 乘法公式练习(无答案)
文档属性
| 名称 | 人教版八年级上册 14.2 乘法公式练习(无答案) | 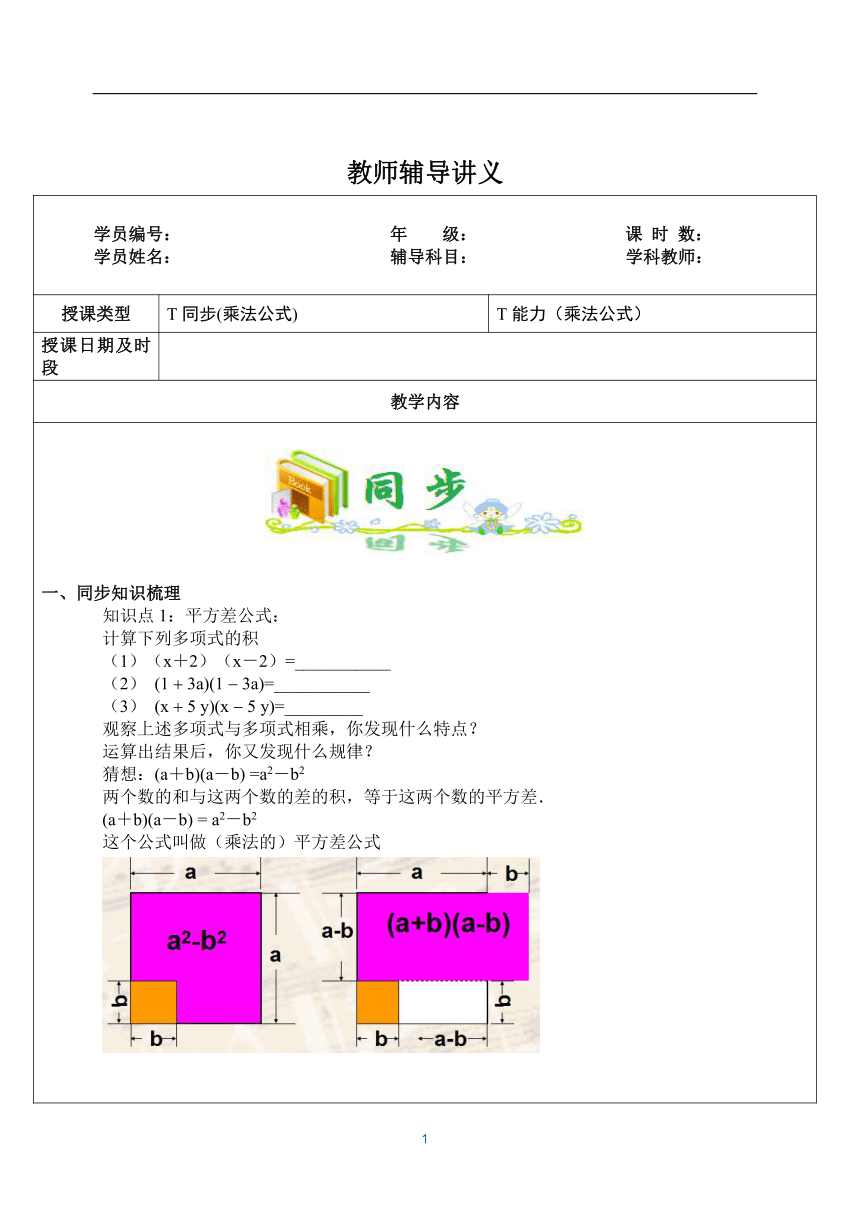 | |
| 格式 | zip | ||
| 文件大小 | 402.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 10:49:07 | ||
图片预览





文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 T同步(乘法公式) T能力(乘法公式)
授课日期及时段
教学内容
同步知识梳理知识点1:平方差公式:计算下列多项式的积(1)(x+2)(x-2)=___________ (2) 1 3a1 3a=___________ (3) x 5 yx 5 y=_________观察上述多项式与多项式相乘,你发现什么特点? 运算出结果后,你又发现什么规律? 猜想:(a+b)(a-b) =a2-b2 两个数的和与这两个数的差的积,等于这两个数的平方差. (a+b)(a-b) = a2-b2 这个公式叫做(乘法的)平方差公式 1.判断下列式子能否用平方差公式计算. (1) a ba c (2) x y y x (3) ab 3x 3x ab m nm n2a b 2b a (6)2x y 2x y 2、判断: (1 ) 2a b2b a 4a 2 b2 (2 ) (3 )3x y 3x y 9x 2 y 2 (4 ) 2x y 2x y 4x 2 y 2 (5 )a 2a 3 a 2 6 (6) x 3y 3 xy 9 3.利用平方差公式计算: (1) 4a 7b4a 7b (2) 2m n2m n (3) (a +3b)(a?3b) (3 +2a)(?3 + 2a) (3x+4) (3x ?4) ?(2x +3) (3x?2) 计算:(1)(y+2)(y2+4)(y-2) (2)69×71; (3)53×47; (4)503×497; (5)40×39 5、填空:(1) 2x 3y2x 3y (2)(4a-1)( )= 16a2-1 (3)( ) (4) 2x 3y 4x2 9 y2 知识点2:完全平方公式(a+b)2=(a+b)(a+b) =a2 +ab +ab +b2 = a2 +2ab+b2 (a-b)2=(a-b) (a-b) = a2 - ab - ab +b2 = a2 - 2ab+b2 公式特点: 1、结果为二次三项式; 2、其中两项为两数的平方和; 3、另一项是两数积的2倍,且与乘式中
间的符号相同。 4、公式中的字母a,b可以表示单项式、多项式等口诀:首平方,尾平方,首尾两倍放中央。 同步题型分析题型1:1、计算(x-y)(-y-x)的结果是( ) A.-x2+y2 B. -x2-y2 C. x2-y2 D. x2+y2 2、计算(x+3y)2-(3x+y)2的结果是( ) A. 8x2-8y2 B. 8y2-8x2 C. 8(x+y)2 D. 8(x-y)23、若x2-y2=100,x+y= -25,则x-y的值是( ) A.5 B. 4 C. -4 D. 以上都不对4、化简(m2+1)(m+1)(m-1)-(m4+1)的值是( ) A. -2m2 B.0 C.-2 D.-1 5.下列运算中,正确的是( ) A.(a+3)(a-3)=a2-3 B.(3b+2)(3b-2)=3b2-4 C.(3m-2n)(-2n-3m)=4n2-9m2 D.(x+2)(x-3)=x2-66.在下列多项式的乘法中,可以用平方差公式计算的是( ) A.(x+1)(1+x) B.(a+b)(b-a) C.(-a+b)(a-b) D.(x2-y)(x+y2) 7、计算(3m+4)(4-3m)的结果是______ 8、若x-y=2,x2-y2=6,则x+y=________. 9、计算(2m+1)(4m2+1)(2m-1)=_____. 10、用简便方法计算:503×497=_______;1.02×0.98=______.11.9.8×10.2=________; 12.(2x+)(2x-)= .13.(2x+y)( 2x-y)= . 14.(3a+2b)(3a-2b) = . 16.如果 a2-b2=10,(a+b)=2,则a - b= . 17、观察下列各式:1×3=22-1,3×5=42-1,5×7=62-1,……请你把发现的规律用含n(n为正整数)的等式表示为_________.计算1.(x+6)(6-x) 2. 3. (- +y)(+y) 5.(2a-b)(2a+b)(4a2+b2); 6.(3a-2b)(9a+6b); 7.(2y-1)(4y2+1)(2y+1) 8.3(2a+1)(-2a+1)-( a-3)(3+a) 9.a4-(1-a)(1+a)(1+a2)(1+a) 题型21.下列式子能成立的是( ) A.(a?b) 2 = a2?ab+b2 ???????????????? ?B.(a+3b)2 = a2+9b2 C.(a+b)2 = a2+2ab+b2 ???????????? ??? ??D.(x+3)(x?3) = x2?x?92.下列多项式乘法中,可以用平方差公式计算的是( ) A.( 2m?3n)(3n? 2m) ????????????? B.(?5xy+4z)(?4z?5xy) C.(?a?b)( b+a) ?????? ? D.(b+c?a)(a?b?c) 3.下列计算正确的是( ) A.( 2a+b)( 2a?b) = 2a2?b2 B.(0.3x+0.2)(0.3x?0.2) = 0.9x2?0.4 C.(a2+3b3)(3b3?a2) = a4?9b6 D.( 3a?bc)(?bc? 3a) = ? 9a2+b 2c2 4.计算(?2y?x)2的结果是( ) A.x2?4xy+4y2 ?? ?B.?x2?4xy?4y 2 ??? C.x2+4xy+4y2 ?? D.?x2+4xy?4y2 5.下列各式中,不能用平方差公式计算的是( ) A.(?2b?5)(2b?5) ??????????? B.(b2+2x2)(2x2?b2)C.(?1? 4a)(1? 4a) ?????????? D.(?m2n+2)(m2n?2) 6.下列各式中,能够成立的等式是( ) A.(x+y) 2 = x2+y2 ???????????????????? ? ?B.(a?b)2 = (b?a)2 C.(x?2y)2 = x2?2xy+y2 ???????????????? D.(a?b)2 =a2+ab+b2例21.计算: (1)( x+y2)( x?y2); (2)(a+2b?c)(a?2b+c); (3)(m?2n)(m2+4n2)(m+2n); (4)(a+2b)( 3a?6b)(a2+4b2); (5)(m+3n)2(m?3n) 2; (6)( 2a+3b)2?2( 2a+3b)(a?2b)+(?a+2b)2.2.利用乘法公式进行简便运算: ①20042; ②999.82; ③(2+1)(22+1)(24+1)(28+1)(216+1)+1 3.①(-xy+5)2 ②(x+3)(x-3)(x2-9) ③(a+2b-c)(a-2b-c) ④(a+b+c)2 4.若a2+b2+4a-6b+13=0,试求ab的值. 5.观察1+3=4=22 1+3+5=9=32 1+3+5+7=16=42 1+3+5+7+9=25=52 …… (1)根据以上规律,猜测1+3+5+7+…+(2n-1)=__________. (2)用文字语言叙述你所发现的规律:___________. 三、课堂达标检测 1. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?bd246f98-bf23-4973-a12c-373afac844d7" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)运用乘法公式计算(a-2)2的结果是( )A.a2-4a+4B.a2-2a+4C.a2-4D.a2-4a-4 2.已知a、b满足a+b=3,ab=2,则a2+b2等于( )A.-1B.2C.5D.6 3.已知x+y=8,xy=,则x-y=( )A.6B.6或-6C.7D.7或-7 4. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?5e97b695-1827-447c-96a7-34bb7fdd6d77" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)若a+b=6,ab=4,则a2-ab+b2的值为( )A.32B.-12C.28D.24 5.若m为大于0的整数,则(m+4)2-(m-4)2一定是( )A.2的倍数B.4的倍数C.8的倍数D.16的倍数 6. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?10847958-e4f6-4fd4-86c6-8753b40c743e" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)已知a-b=3,则代数式a2-b2-6b的值为( )A.3B.6C.9D.12 7. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?10d29f57-b590-4872-8ce9-342c6d34d633" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)计算(a-1)2正确的是( )A.a2-a+1B.a2-2a+1C.a2-2a-1D.a2-1 8.下列关于962的计算方法正确的是( )A.962=(100-4)2=1002-42=9984 B.962=(95+1)(95-1)=952-1=9024 C.962=(90+6)2=902+62=8136 D.962=(100-4)2=1002-2×4×100+42=9216 9. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?79993d41-bab6-4ed9-9f01-b24bb2b266ac" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)若关于x的二次三项式x2-ax+36是一个完全平方式,那么a的值是( )A.12B.±12C.6D.±6 10. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?0fa3c328-238d-4eb4-b3c4-dce730d0b5df" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)计算20142-4024×2014+20122等于( )A.2B.4C.6D.8 11. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?8b64caa8-7b86-423b-bbc1-4ccb661db9dc" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)若(2a±3)2=4a2+(k-1)a+9,则k的值为( )A.±12B.±11C.±13D.-11或13 12.已知a2-b2=80,a-b=8,则a+b=( )A.72B.88C.10D.20 13.下列各式能用完全平方公式计算的是( ) A.(3a+2b)(3a-2b)B.(3a+2b)(2b-3a) C.(3a-2b)(2b-3a)D.(3a-2b)(-3a-2b) 14. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?bf68a4bd-7a63-4056-9731-d539a5b4da72" \o "此年份及地区表示:该试题最新出现所在的试卷年份及地区" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)若a+b=7,ab=10,则a2+b2的值是( )A.5B.21C.29D.85 15. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?84325859-0744-4bf0-ba8a-f971fedb7c0f" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)正方形的边长增加了2cm,面积相应增加了24cm2,则这个正方形原来的面积是( )A.15cm2B.25cm2C.36cm2D.49cm2 16. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?70946cfc-c174-4227-a341-f139853b91c2" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如利用图1可以得到(a+b)2=a2+2ab+b2,那么利用图2所得到的数学等式是( )
A.(a+b+c)2=a2+b2+c2 B.(a+b+c)2=a2+b2+c2+2ab+2ac+2bc C.(a+b+c)2=a2+b2+b2+ab+ac+bc D.(a+b+c)2=2a+2b+2c 17. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?d9c0d9f5-61a1-404d-9acc-19c3f3a9bf1c" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)如图所示的是用4个全等的小长方形与1个小正方形密铺而成的正方形图案,已知该图案的面积为49,小正方形的面积为4,若分别用x、y(x>y)表示小长方形的长和宽,则下列关系式中不正确的是( )A.x+y=7B.x-y=2C.x2+y2=7D.4xy+4=49 18.已知x2+2(m-1)x+9是一个完全平方式,则m的值为( )A.4B.4或-2C.±4D.-2 19.若x2+kx+81是一个完全平方式,则k的值为( )A.18B.-18C.±18D.±9 20. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?1444e755-460f-44a2-88ca-d2132ab43e58" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)如果x2+6x+n2是一个完全平方式,则n值为( )A.3B.-3C.6D.±3 21. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?624c189d-8fe7-4b4d-9124-8e6ceb4721e2" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)如果多项式y2-4my+4是完全平方式,那么m的值是( )A.1B.-1C.±1D.±2 22. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?7469b8cc-74fc-4a24-aad0-9254c617bc21" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)下列式子是完全平方式的是( )A.a2+2ab-b2B.a2+2a+1C.a2+ab+b2D.a2+2a-1 23.若4x2+(a-1)xy+9y2是完全平方式,则a的值是( ) A.7或-5B.13或-11C.-13或14D.-7或-5 24. (?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?dcc8c16d-e2ef-4cce-bb0a-2181f33425a3" \o "此年份及地区表示:该试题最新出现所在的试卷年份及地区" \t "http:?/??/?www.jyeoo.com?/?math?/?ques?/?_blank?)若4a2+2kab+16b2是完全平方式,那么k的值是( ) A.8B.±8C..16D.±16 25.若x2-4y2=-15,x+2y=3,则y2= . 26.已知x2-y2=12,x-y=2,则xy的值是 . 27.若x+y=2,x2-y2=10,则3x-y= . 28.a2-b2=24,a-b=6,则a+b的值为 4,a= 5,b= . 29. 用乘法公式计算: (1)5012; (2)99.82; (3)60×59; (4)2 0052-2 004×2 006. 30.计算: (1)(a2+1)(a2-1)-(-a2)·a2; (2)(2a-b)(2a+b)-(-3a-b)(-3a+b); (3)x2-(4-x)2; (4)(3x-2y)2-4(2x-y)(x-y). 31.计算: (1)(1.2x-y)(-y-1.2x); (2)15×(-14); (3)[2x2-(x+y)(x-y)][(z-x)(x+z)+(y-z)(y+z)]; (4)(a-2b+3c)(a+2b-3c). 32.(1)已知x+y=6,xy=4,求①x2+y2,②(x-y)2,③x2+xy+y2的值. (2)已知a(a-3)-(a2-3b)=9,求-ab的值. 33.已知(a+b)2=7,(a-b)2=4,求a2+b2和ab的值. 34.已知△ABC的三边a、b、c满足a2+b2+c2-ab-bc-ac=0,试判断△ABC的形状. 35.图15-3-1为杨辉三角系数表部分,它的作用是可以按规律写出形如(a+b)n(其中n为正整数)展开式的系数,请你仔细观察下表中的规律,填出(a+b)4展开式中所缺的系数. 图15-3-1 (a+b)=a+b, (a+b)2=a2+2ab+b2, (a+b)3=a3+3a2b+3ab2+b3,(a+b)4=a2+_________a3b+_________a2b2+_________ab3+b4. 36.大家已经知道,完全平方公式和平方差公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如:2x(x+y)=2x2+2xy就可以用图15-3-2(1)的面积表示. 图15-3-2 (1)请写出图(2)所表示的代数恒等式:__________; (2)请写出图(3)所表示的代数恒等式:__________; (3)试画出一个几何图形,使它的面积能表示(x+y)(x+3y)=x2+4xy+3y2. 37.如图15-3-3所示,长方形ABCD被分成六个大小不一的正方形,已知中间一个小正方形面积为4,求长方形ABCD中最大正方形与最小正方形的面积之差. 图15-3-3
1
