人教版七年级数学下册 7.2.2用坐标表示平移同步课件 (65张)
文档属性
| 名称 | 人教版七年级数学下册 7.2.2用坐标表示平移同步课件 (65张) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 00:00:00 | ||
图片预览





文档简介
(共65张PPT)
知识点一????坐标系中点的平移
点P(x,y)的平移方式(a>0,b>0) 平移后点的坐标
点的
平移
方式 左右平移 向右平移a个单位 (x+a,y)
向左平移a个单位 (x-a,y)
上下平移 向上平移b个单位 (x,y+b)
向下平移b个单位 (x,y-b)
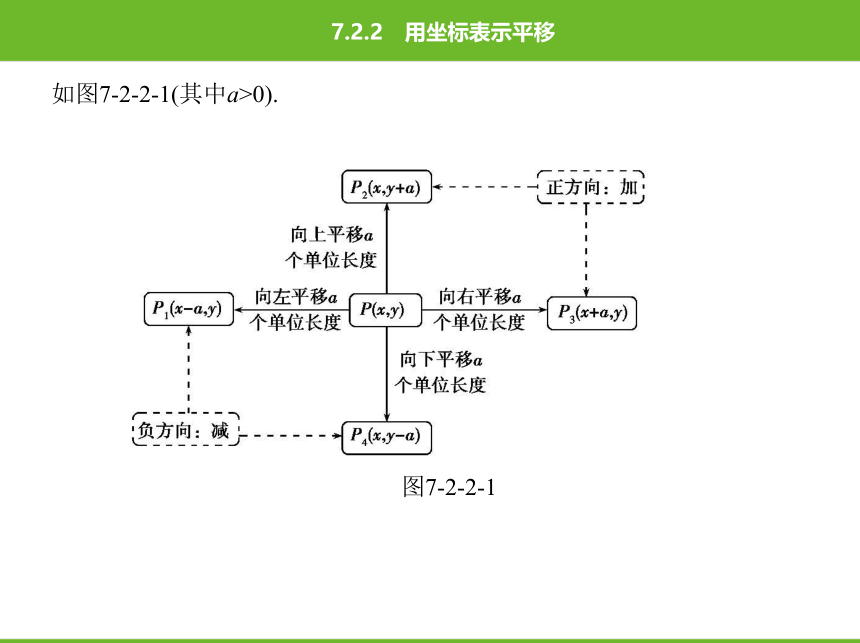
如图7-2-2-1(其中a>0).
?
图7-2-2-1
例1 把点M(-3,1)向上平移2个单位得到点N,则点N的坐标为 ????,再
把点N向左平移4个单位得到点Q,则点Q的坐标为 ????.
解析 把点M(-3,1)向上平移2个单位,则横坐标不变,纵坐标加上2,所以N(-
3,3);把点N(-3,3)向左平移4个单位,则纵坐标不变,横坐标减去4,得Q(-7,3).
答案 (-3,3);(-7,3)
知识点二????坐标系中图形的平移
坐标系中图形的平移是指在平面直角坐标系中,保持坐标轴不动,只进
行图形的整体移动.在平移变换中,图形的形状和大小都不变,变的仅仅是
图形的位置.
(1)图形中所有点的纵坐标保持不变,横坐标分别加k.
当k>0时,原图形向右平移k个单位长度;当k<0时,原图形向左平移|k|个单位
长度.
(2)图形中所有点的横坐标保持不变,纵坐标分别加k.
当k>0时,原图形向上平移k个单位长度;当k<0时,原图形向下平移|k|个单位
长度.
重点剖析 (1)图形是由点组成的,图形的平移可转化为点的平移,通过点
的坐标的变化来实现图形的平移.
(2)决定平移的因素:平移的方向和平移的距离.
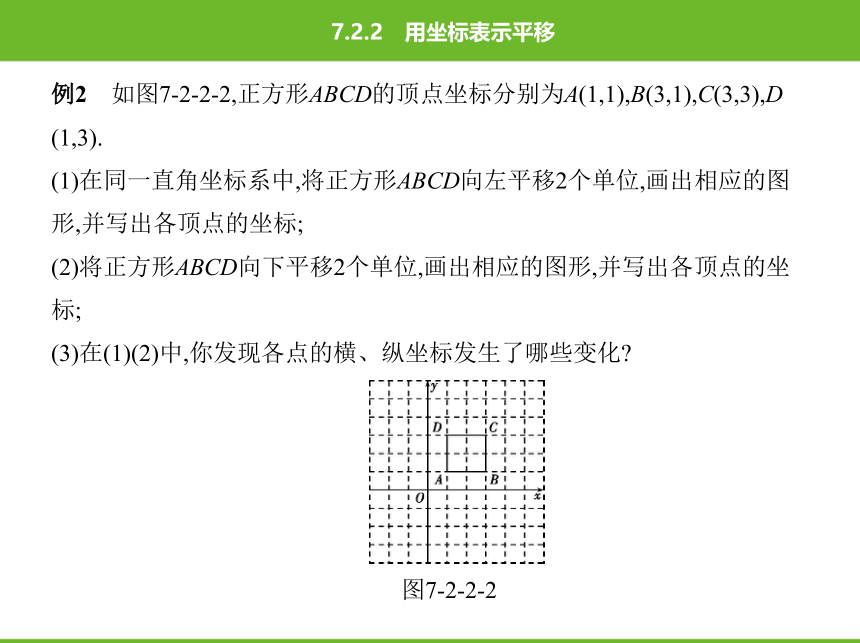
例2 如图7-2-2-2,正方形ABCD的顶点坐标分别为A(1,1),B(3,1),C(3,3),D
(1,3).
(1)在同一直角坐标系中,将正方形ABCD向左平移2个单位,画出相应的图
形,并写出各顶点的坐标;
(2)将正方形ABCD向下平移2个单位,画出相应的图形,并写出各顶点的坐
标;
(3)在(1)(2)中,你发现各点的横、纵坐标发生了哪些变化?
?
图7-2-2-2
解析 (1)在同一直角坐标系中,将正方形ABCD向左平移2个单位,得到如
图7-2-2-3中的正方形A'B'C'D'.正方形A'B'C'D'的各顶点坐标为A'(-1,1),B'(1,
1),C'(1,3),D'(-1,3).
?
图7-2-2-3
(2)在同一直角坐标系中,将正方形ABCD向下平移2个单位,得到如图7-2-2-
3中的正方形A″B″C″D″.正方形A″B″C″D″的各顶点坐标为A″
(1,-1),B″(3,-1),C″(3,1),D″(1,1).
(3)在(1)中,各点的纵坐标不变,横坐标都减小2;在(2)中,各点的横坐标不变,
纵坐标都减小2.
点拨????对一个图形进行平移,这个图形上所有点的坐标都发生相同的变化,
即图形的平移也就是把图形上的点进行平移.因此,掌握好点的坐标的平移
规律是解决此类问题的关键.
题型一????图形的平移与坐标变化
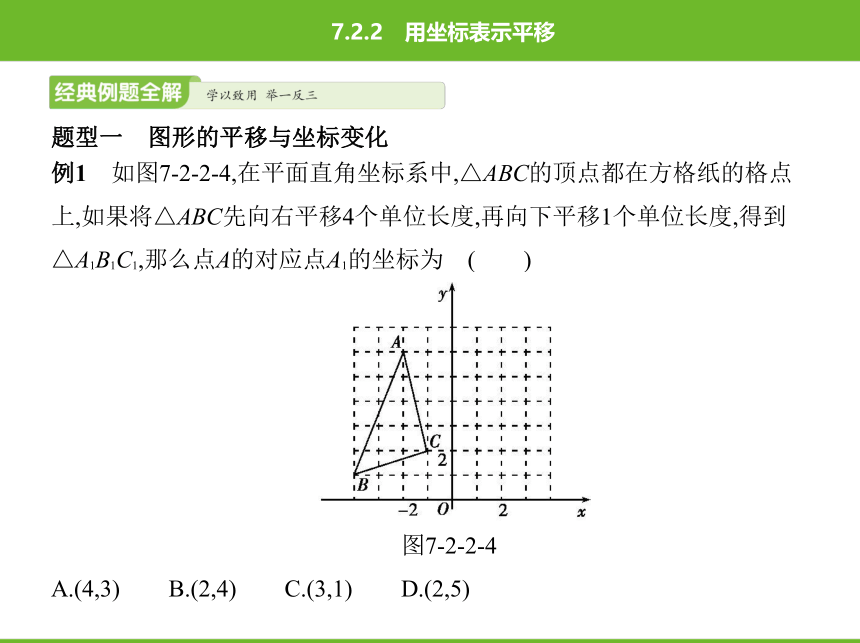
例1 如图7-2-2-4,在平面直角坐标系中,△ABC的顶点都在方格纸的格点
上,如果将△ABC先向右平移4个单位长度,再向下平移1个单位长度,得到
△A1B1C1,那么点A的对应点A1的坐标为?( )
?
图7-2-2-4
A.(4,3) ????B.(2,4) ????C.(3,1) ????D.(2,5)
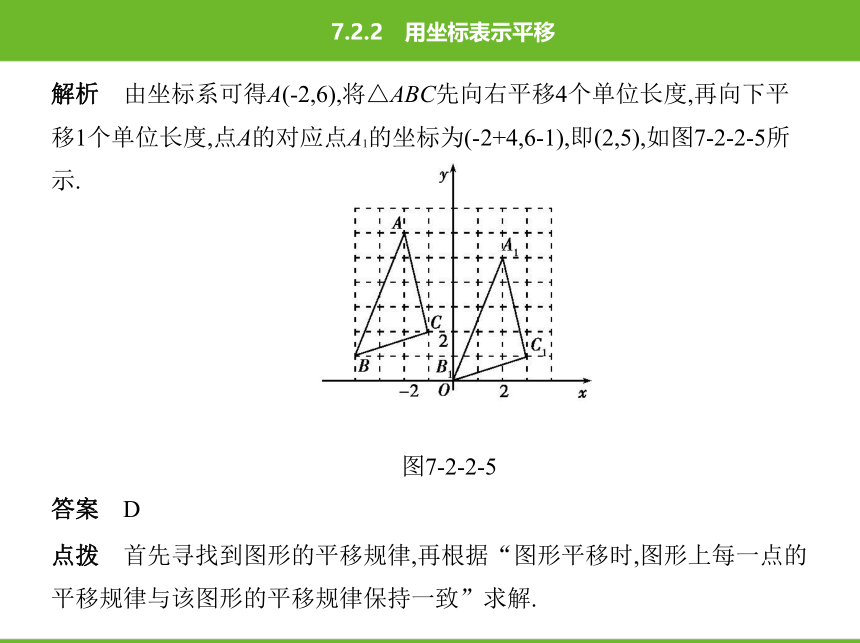
解析 由坐标系可得A(-2,6),将△ABC先向右平移4个单位长度,再向下平
移1个单位长度,点A的对应点A1的坐标为(-2+4,6-1),即(2,5),如图7-2-2-5所
示.
?
图7-2-2-5
答案????D
点拨 首先寻找到图形的平移规律,再根据“图形平移时,图形上每一点的
平移规律与该图形的平移规律保持一致”求解.
题型二????平移作图
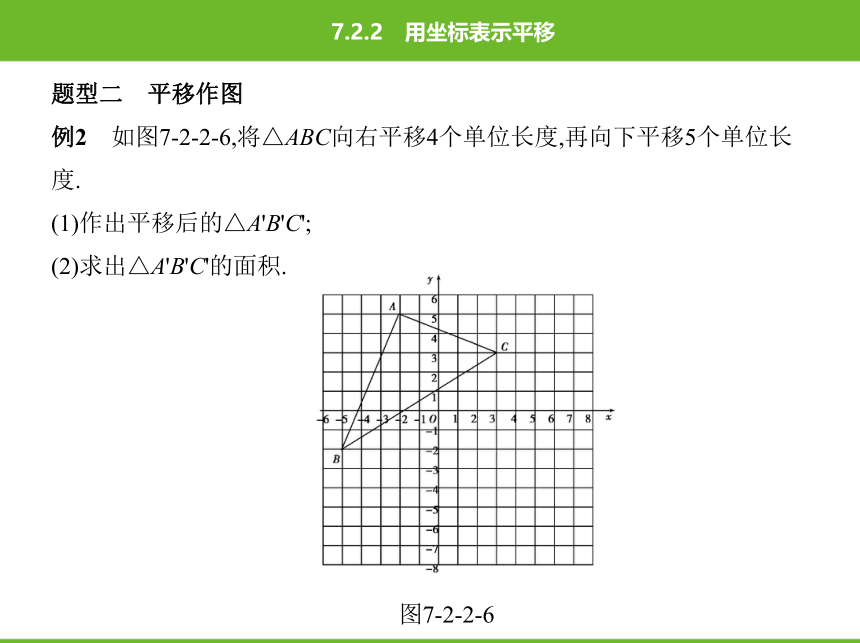
例2 如图7-2-2-6,将△ABC向右平移4个单位长度,再向下平移5个单位长
度.
(1)作出平移后的△A'B'C';
(2)求出△A'B'C'的面积.
?
图7-2-2-6
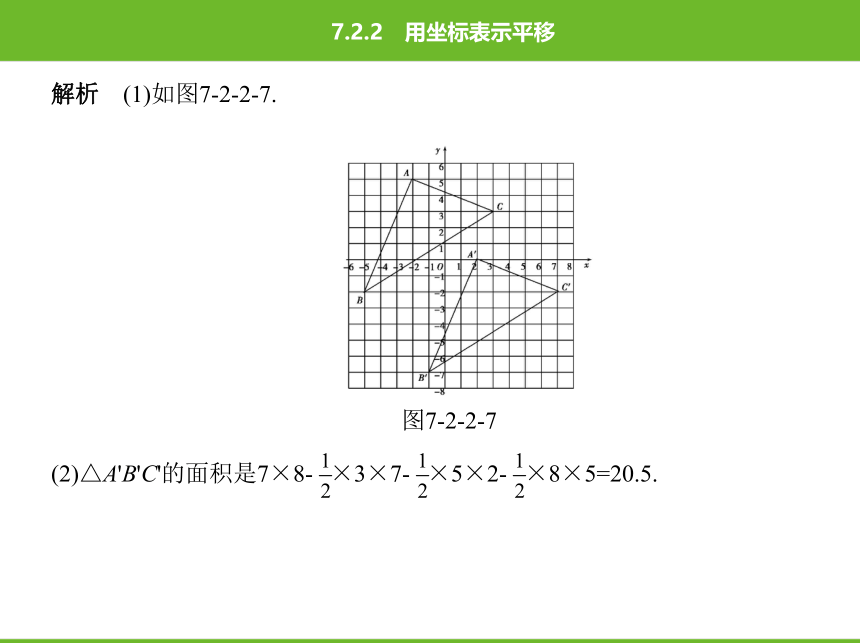
解析 (1)如图7-2-2-7.
?
图7-2-2-7
(2)△A'B'C'的面积是7×8-?×3×7-?×5×2-?×8×5=20.5.
棋盘上的数学
典例剖析????
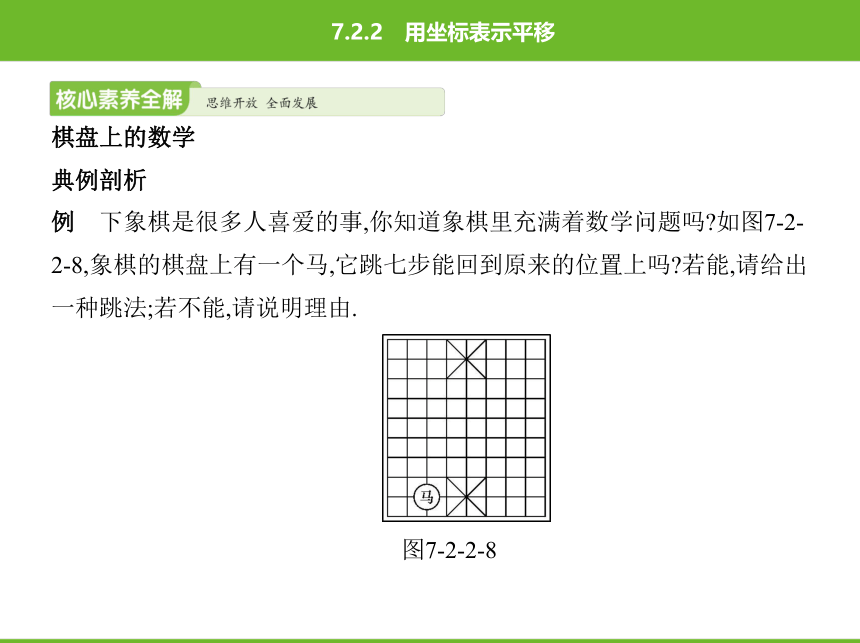
例 下象棋是很多人喜爱的事,你知道象棋里充满着数学问题吗?如图7-2-
2-8,象棋的棋盘上有一个马,它跳七步能回到原来的位置上吗?若能,请给出
一种跳法;若不能,请说明理由.
?
图7-2-2-8
素养呈现 逻辑推理是指从一些事实和命题出发,依据逻辑规则推出其他
命题的素养.主要包括两类:一类是从特殊到一般的推理,推理形式主要有
归纳、类比;一类是从一般到特殊的推理,推理形式主要有演绎.本题以下
象棋为背景,通过逻辑推理来说明马跳七步不可能回到原来的位置.
解析 无论怎么跳,马都不能回到原来的位置,理由如下:
如图7-2-2-9,我们可在棋盘上建立直角坐标系,并设这个马所在的位置P的
坐标为(x0,y0),那么,马跳一步后的位置的坐标应为(x0+x1,y0+y1),这里的x1和y1
只可能分别是1,-1,2,-2这四个数中的一个(想一想,为什么).
同样,跳第二步后,马所在的位置的坐标应为(x0+x1+x2,y0+y1+y2),这里的x2和y2
也只可能是1,-1,2,-2中的一个,依此类推,跳七步后,马所在的位置的坐标为
(x0+x1+x2+x3+x4+x5+x6+x7,y0+y1+y2+y3+y4+y5+y6+y7),如果这时马又回到原来的
位置(x0,y0),那么有x0+x1+x2+x3+x4+x5+x6+x7=x0,y0+y1+y2+y3+y4+y5+y6+y7=y0,也即
x1+x2+x3+x4+x5+x6+x7=0,y1+y2+y3+y4+y5+y6+y7=0,
将两式相加,有(x1+y1)+(x2+y2)+(x3+y3)+(x4+y4)+(x5+y5)+(x6+y6)+(x7+y7)=0.
上式中14个数只能分别取1,-1,2,-2中的一个,根据象棋中“马”跳一步的
规则可知x1+y1,x2+y2,x3+y3,x4+y4,x5+y5,x6+y6,x7+x7这七个数只能分别取1,-1,3,-3
中的一个,但是无论怎样取,由于奇数个奇数相加的和为奇数,所以这样取
出的七个数的和不可能等于0,故马跳七步不可能回到原来的位置.
?
图7-2-2-9
素养解读 逻辑推理是得到数学结论、构建数学体系的重要方式,是数学
严谨性的基本保证,是人们在数学活动中进行交流的基本思维品质.在逻辑
推理核心素养的形成过程中,学生能够发现问题和提出命题;能掌握推理的
基本形式,探索和表述论证过程;能理解数学知识之间的联系,建构知识框
架,形成有论据、有条理、合乎逻辑的思维品质,增强数学交流能力.
知识点一????坐标系中点的平移
1.已知点A(-2,4),将点A往上平移2个单位长度,再往左平移3个单位长度得
到点A',则点A'的坐标是?( )
A.(-5,6) ????B.(1,2) ????C.(1,6) ????D.(-5,2)
答案????A????点A往上平移2个单位长度,再往左平移3个单位长度后,点的坐
标为(-2-3,4+2),即A'(-5,6),故选A.
2.(独家原创试题)在平面直角坐标系中,将点P(-3,4)平移至原点,则平移方
式可以是?( )
A.先向左平移3个单位长度,再向上平移4个单位长度
B.先向右平移4个单位长度,再向上平移3个单位长度
C.先向左平移3个单位长度,再向下平移4个单位长度
D.先向右平移3个单位长度,再向下平移4个单位长度
答案????D 将点P(-3,4)的横坐标加3,纵坐标减4可平移至原点(0,0),故可以
先向右平移3个单位长度,再向下平移4个单位长度.
知识点二????坐标系中图形的平移
3.已知△ABC在平面直角坐标系中的位置如图7-2-2-1所示,将△ABC先向
下平移5个单位,再向左平移2个单位,则平移后C点的坐标是?( )
?
图7-2-2-1
A.(5,-2) ????B.(1,-2) ????C.(2,-1) ????D.(2,-2)
答案????B ∵△ABC先向下平移5个单位,再向左平移2个单位,∴平移后点
C的横坐标为3-2=1,纵坐标为3-5=-2,∴平移后点C的坐标为(1,-2).故选B.
4.(独家原创试题)平面直角坐标系中,A(2,1),B(4,1),将线段AB平移,使得AB
的中点落在对应点(-1,-2)的位置,则点A的对应点的坐标为 ????.
答案 (-2,-2)
解析 由A(2,1),B(4,1)可知AB∥y轴,易知AB的中点坐标为(3,1),由(3,1)平
移到(-1,-2),可知横坐标减4,纵坐标减3,故点A的对应点为(2-4,1-3),即(-2,-
2).
5.如图7-2-2-2,方格纸中每个小方格都是边长为1个单位长度的正方形,在
平面直角坐标系中,已知点A(1,0),B(4,0),C(3,3),D(1,4).
(1)描出A、B、C、D四点的位置,并顺次连接A、B、C、D、A;
(2)四边形ABCD的面积是 ????;
(3)把四边形ABCD向左平移5个单位,再向上平移1个单位得到四边形A'B'C'
D',在图中画出四边形A'B'C'D',并写出A'、B'、C'、D'的坐标.
?
图7-2-2-2
解析 (1)如图.
?
(2)四边形ABCD的面积是?.
(3)四边形A'B'C'D'如图.其中A'(-4,1)、B'(-1,1)、C'(-2,4)、D'(-4,5).
1.(2018湖北黄石中考)如图,将“笑脸”图标向右平移4个单位,再向下平移
2个单位,点P的对应点P'的坐标是?( )
A.(-1,6) ????B.(-9,6) ????
C.(-1,2) ????D.(-9,2)
答案????C????由题图知P(-5,4),向右平移4个单位,再向下平移2个单位,点P的
对应点P'的坐标是(-1,2),故选C.
2.将点P(m+2,2m+4)向右平移1个单位到P',且P'在y轴上,那么P'的坐标是?
( )
A.(-2,0) ????B.(0,-2) ????C.(1,0) ????D.(0,1)
答案????B????点P(m+2,2m+4)向右平移1个单位后的坐标为(m+3,2m+4),所以P
'(m+3,2m+4),由于该点在y轴上,所以m+3=0,m=-3,所以2m+4=-2.所以P'(0,-
2).
3.点M(4,3)向 ????(填“上”“下”“左”或“右”)平移 ????个
单位后落在y轴上;向 ????(填“上”“下”“左”或“右”)平移 ????
????个单位后落在x轴上.
答案 左;4;下;3
解析 根据点的坐标的平移规律,点M(4,3)要平移至y轴上,则横坐标要减4,
故向左平移4个单位;点M(4,3)要平移至x轴上,则纵坐标要减3,故向下平移3
个单位.
4.(2016黑龙江哈尔滨双城期末)在同一坐标系中,图形a是由图形b向上平
移3个单位长度得到的,如果图形a中点A的坐标为(4,-2),则图形b中与点A对
应的点A'的坐标为 ????.
答案 (4,1)
解析 图形向上平移3个单位长度,图形中的点的坐标的变化是横坐标不
变,纵坐标加上3.
5.(2017广东深圳一模)如图,直角坐标系中,△ABC的顶点都在网格点上,其
中C点坐标为(1,2).(8分)
(1)点A的坐标是 ????,点B的坐标是 ????;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'
C',画出△A'B'C',并写出△A'B'C'的三个顶点的坐标;
(3)求△ABC的面积.
解析 (1)(2,-1);(4,3).
(2)画出的△A'B'C'如图所示;A'(0,0),B'(2,4),C'(-1,3).
?
(3)△ABC的面积=3×4-?×2×4-?×3×1-?×3×1=5.
1.(2016山东青岛中考)如图7-2-2-3,线段AB经过平移得到线段A'B',其中
点A,B的对应点分别为点A',B',这四个点都在格点上.若线段AB上有一个点
P(a,b),则点P在A'B'上的对应点P'的坐标为?( )
?
图7-2-2-3
A.(a-2,b+3) ????B.(a-2,b-3)
C.(a+2,b+3) ????D.(a+2,b-3)
答案????A????由题图可知线段AB向左平移2个长度单位,再向上平移3个长度
单位得到线段A'B',由此可知线段AB上的点P(a,b)的对应点P'的坐标为(a-2,
b+3),故选A.
2.如图7-2-2-4所示,四边形ABCO中,AB∥OC,BC∥AO,A、C两点的坐标分
别为(-?,?)、(-2?,0),A、B两点间的距离等于O、C两点间的距离.
(1)点B的坐标为 ????;
(2)将这个四边形向下平移2?个单位长度后得到四边形A'B'C'O',请你写出
平移后四边形四个顶点的坐标.
图7-2-2-4
解析 (1)∵C点的坐标为(-2?,0),∴OC=2?.
∵AB∥OC,AB=OC,∴将A点向左平移2?个单位得到B点,又∵A点的坐标
为(-?,?),
∴B点的坐标为(-?-2?,?),即(-3?,?).
(2)∵将四边形ABCO向下平移2?个单位长度后得到四边形A'B'C'O',∴A'
点的坐标为(-?,-?),B'点的坐标为(-3?,-?),C'点的坐标为(-2?,-2?),
O'点的坐标为(0,-2?).
1.(2019福建厦门模拟)在平面直角坐标系xOy中,点P(0,1)第1次向右平移1
个单位长度,向下平移2个单位长度至点P1(1,-1);第2次向右平移1个单位长
度,向上平移3个单位长度至点P2(2,2);第3次向右平移1个单位长度,向下平
移4个单位长度至点P3(3,-2);第4次向右平移1个单位长度,向上平移5个单
位长度至点P4(4,3),……,按照此规律,点P2 019的坐标是?( )
A.(2 019,1 009) ????B.(2 019,-1 009)
C.(2 019,1 010) ????D.(2 019,-1 010)
答案????D 根据题意,可知点P第n次移动的规律是:向右平移1个单位长度,
向上或向下平移(n+1)个单位长度,其中n为奇数时向下,n为偶数时向上.因
此,点P第2 019次平移至点P2 019的横坐标是0+1×2 019=2 019,纵坐标是1-2+
3-4+5-6+7-…+2 019-2 020=-1 010,
即点P2 019的坐标是(2 019,-1 010).
2.如图,△A'B'C'是由△ABC经过某种变换后得到的图形,如果△ABC中有一
点P的坐标为(a,2),那么变换后它的对应点Q的坐标为 ????.
?
答案 (a+5,-2)
解析 由题图可知,A(-4,3),A'(1,-1),由点A向右平移5个单位,向下平移4个
单位可得点A',
故P(a,2)的对应点Q的坐标为(a+5,-2).
3.如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点
的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速
度沿着O→A→B→C→O的路线移动.
(1)点B的坐标为 ????;
(2)当点P移动了4秒时,求出点P的坐标;
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
解析 (1)根据长方形的性质,可得AB与y轴平行,BC与x轴平行,故点B的坐
标为(4,6).
(2)∵P的运动速度为每秒2个单位长度,∴当点P移动了4秒时,共运动了8个
单位长度,此时点P位于AB上,且坐标为(4,4).
(3)当P在AB上时,P运动了4+5=9个单位长度,此时点P运动了9÷2=4.5秒;
当P在OC上时,P运动了4+6+4+1=15个单位长度,此时点P运动了15÷2=7.5
秒.
一、选择题
1.(2019天津和平期末,8,★☆☆)在平面直角坐标系中,将点P先向左平移2
个单位长度,再向下平移3个单位长度后的对应点的坐标为(-1,3),则点P的
坐标为?( )
A.(2,3) ????B.(-2,-3) ????C.(2,5) ????D.(1,6)
答案????D 设点P的坐标为(x,y),则有x-2=-1,y-3=3,得x=1,y=6,所以点P的坐
标为(1,6).
2.(2019安徽合肥庐江期末,10,★★☆)如图7-2-2-5,点A1(1,1),点A1向上平移
1个单位,再向右平移2个单位,得到点A2;点A2向上平移2个单位,再向右平移
4个单位,得到点A3;点A3向上平移4个单位,再向右平移8个单位,得到点A4,…
…,按这个规律平移得到点An,则点An的横坐标为?( )
?
图7-2-2-5
A.2n ????B.2n-1 ????C.2n-1 ????D.2n+1
答案????C 由题意知,点A1的横坐标为1=21-1,点A2的横坐标为3=22-1,点A3的
横坐标为7=23-1,点A4的横坐标为15=24-1,……,按这个规律平移得到点An的
横坐标为2n-1.
二、填空题
3.(2018湖北天门模拟,13,★★☆)如图7-2-2-6,点A、B的坐标分别为(1,2)、
(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为 ????
????.
?
图7-2-2-6
答案 (4,2)
解析 易知OD=3,即△AOB沿x轴向右平移3个单位长度得到△CDE,∴点
C的坐标为(4,2).
4.(2017江西景德镇二中期末,10,★★☆)在平面直角坐标系中,△A'B'C'是
由△ABC平移得到的,△ABC中任意一点P(x0,y0)经过平移后的对应点为P'(x
0+7,y0+2),若A'的坐标为(5,3),则它的对应点A的坐标为 ????.
答案 (-2,1)
解析 根据题意,可得△ABC到△A'B'C'的平移规律为向右平移7个单位,向
上平移2个单位,∵A'的坐标为(5,3),∴它的对应点A的坐标为(-2,1).
1.(2018安徽合肥六中期末,3,★☆☆)在平面直角坐标系中,点A'(2,-3)可以
由点A(-2,3)通过两次平移得到,则下列说法正确的是?( )
A.先向左平移4个单位长度,再向上平移6个单位长度
B.先向右平移4个单位长度,再向上平移6个单位长度
C.先向左平移4个单位长度,再向下平移6个单位长度
D.先向右平移4个单位长度,再向下平移6个单位长度
答案????D 把点A(-2,3)先向右平移4个单位长度,再向下平移6个单位长度
得到点A'(2,-3).故选D.
2.(2019四川广安期末,7,★★☆)△ABC所在平面内任意一点P(a,b)经过平
移后的对应点为P1(c,d),已知A(2,3)经过此次平移后的对应点为A1(5,-1),则a
+b-c-d的值为?( )
A.-5 ????B.5
C.-1 ????D.1
答案????D 由A(2,3)先向右平移3个单位长度,再向下平移4个单位长度可得
A1(5,-1),所以c=a+3,d=b-4,即a-c=-3,b-d=4,则a+b-c-d=-3+4=1.
3.(2019广东广州番禺二中期中,10,★★☆)如图,在平面直角坐标系中,点P
(1,0)第1次向上跳动1个单位至点P1(1,1),第2次向左跳动2个单位至点P2(-1,
1),第3次向上跳动1个单位至点P3(-1,2),第4次向右跳动3个单位至点P4(2,2),
第5次又向上跳动1个单位至点P5(2,3),……,依此规律跳动下去,点P200的坐
标是?( )
?
A.(51,100) ????B.(50,100) C.(-50,100) ????D.(-51,100)
答案????A 由题中规律可知P200的坐标与P4(2,2),P8(3,4),P12(4,6),……,P4n(n+
1,2n)的规律一致,而200÷4=50,故P200的坐标为(50+1,2×50),即(51,100).
4.(2019四川南充嘉陵二中月考,25,★★★)如图,在平面直角坐标系中,同时
将点A(-1,0)、B(3,0)向上平移2个单位长度,再向右平移1个单位长度,分别
得到A、B的对应点C、D.连接AC,BD.
(1)求点C、D的坐标,并描出点A、B、C、D,求四边形ABDC面积;
(2)在坐标轴上是否存在点P,连接PA、PC,使S△PAC=S四边形ABDC?若存在,求出点
P的坐标;若不存在,请说明理由.
解析 (1)点C的坐标为(-1+1,0+2),即(0,2),点D的坐标为(3+1,0+2),即(4,2),
如图所示,根据平移的性质,可知四边形ABDC为平行四边形,则S四边形ABDC=2×
4=8.
?
(2)存在.当P在x轴上时,∵S△PAC=S四边形ABDC,
∴?AP·OC=8,∵OC=2,∴AP=8,
∴点P的坐标为(7,0)或(-9,0);
当P在y轴上时,∵S△PAC=S四边形ABDC,
∴?CP·OA=8,∵OA=1,∴CP=16,
∴点P的坐标为(0,18)或(0,-14).
综上,点P的坐标为(7,0)或(-9,0)或(0,18)或(0,-14).
一、选择题
1.(2019辽宁大连中考,4,★☆☆)在平面直角坐标系中,将点P(3,1)向下平移
2个单位长度,得到的点P'的坐标为?( )
A.(3,-1) ????B.(3,3) ????C.(1,1) ????D.(5,1)
答案????A 将点P(3,1)向下平移2个单位长度,得到的点P'的坐标为(3,1-2),
即(3,-1).
2.(2019海南中考,8,★☆☆)如图7-2-2-7,在平面直角坐标系中,已知点A(2,
1),点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标
为?( )
?
图7-2-2-7
A.(-1,-1) ????B.(1,0) ????C.(-1,0) ????D.(3,0)
答案????C ∵将点A(2,1)向左平移4个单位,向上平移1个单位可得点A1(-2,
2),∴点B的对应点B1的坐标为(3-4,-1+1),即(-1,0).
3.(2019甘肃兰州中考,10,★☆☆)如图7-2-2-8,在平面直角坐标系xOy中,将
四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(-3,5),B(-
4,3),A1(3,3),则点B1的坐标为?( )
?
图7-2-2-8
A.(1,2) ????B.(2,1)
C.(1,4) ????D.(4,1)
答案????B ∵3=-3+6,3=5-2,∴四边形ABCD先向下平移2个单位长度,再向
右平移6个单位长度,∴B1的坐标是(2,1),故选B.
二、填空题
4.(2018江苏宿迁中考,14,★☆☆)在平面直角坐标系中,将点(3,-2)先向右平
移2个单位长度,再向上平移3个单位长度,则所得点的坐标是 ????.
答案 (5,1)
解析 将点(3,-2)先向右平移2个单位长度,
得到点(5,-2),再向上平移3个单位长度,
所得点的坐标是(5,1).
1.(2019四川成都中考,4,★☆☆)在平面直角坐标系中,将点(-2,3)向右平移4
个单位长度后得到的点的坐标为?( )
A.(2,3) ????B.(-6,3)
C.(-2,7) ????D.(-2,-1)
答案????A 将点(-2,3)向右平移4个单位长度得到的点的坐标为(-2+4,3),即
(2,3).
2.(2017湖南邵阳中考,10,★☆☆)如图,三架飞机 P,Q,R 保持编队飞行,某时
刻在坐标系中的坐标分别为(-1,1),(-3,1),(-1,-1).30 秒后,飞机 P 飞到 P'(4,3)
的位置,则飞机 Q,R 的位置Q',R'分别为?( )
?
A.Q'(2,3),R'(4,1) ????B.Q'(2,3),R'(2,1)
C.Q'(2,2),R'(4,1) ????D.Q'(3,3),R'(3,1)
答案????A????因为保持编队飞行,且点(-1,1)移动到P'(4,3)向右平移了5个单
位,向上平移了2个单位,所以点(-3,1),(-1,-1)平移后的坐标分别为(2,3),(4,1),
故选A.
3.(2017辽宁大连中考,7,★☆☆)在平面直角坐标系xOy中,线段AB的两个端
点坐标分别为A(-1,-1),B(1,2).平移线段AB,得到线段A'B'.已知点A'的坐标为
(3,-1),则点B'的坐标为?( )
A.(4,2) ????B.(5,2) ????C.(6,2) ????D.(5,3)
答案????B 由于A(-1,-1),A'(3,-1),说明线段AB向右平移了4个单位,因此B点
也相应地向右平移了4个单位,因此B'(5,2).故选B.
4.(2017广西百色中考,16,★★☆)如图,在正方形OABC中,O为坐标原点,点
C在y轴正半轴上,点A的坐标为(2,0),将正方形OABC沿着OB方向平移?OB
个单位,则点C的对应点的坐标是 ????.
?
答案 (1,3)
解析 易知OC=OA=2,所以C(0,2),将正方形OABC沿着OB方向平移?OB个
单位,即将正方形OABC先向右平移1个单位,再向上平移1个单位,故点C的
对应点的坐标是(1,3).
5.(2015山东青岛中考,10,★☆☆)如图,将平面直角坐标系中“鱼”的每个
“顶点”的纵坐标保持不变,横坐标分别变为原来的?,那么点A的对应点A
'的坐标是 ????.
?
答案 (2,3)
解析 由题图可知,点A变化前的坐标为(6,3),将纵坐标保持不变,横坐标变
为原来的?,则点A的对应点A'的坐标是(2,3).
在由边长为1的小正方形组成的网格中,把一个点先沿水平方向平移|a|
格(当a为正数时,表示向右平移;当a为负数时,表示向左平移),再沿竖直方
向平移|b|格(当b为正数时,表示向上平移;当b为负数时,表示向下平移),得
到一个新的点,我们把这个过程记为(a,b),例如在图7-2-2-9①中,从A到B记
为:A→B(+1,+3);从C到D记为:C→D(+1,-3).
请回答下列问题:
(1)如图7-2-2-9①,若点A的运动路线为:A→B→D→A,请计算点A运动的总
路程;
(2)若点A运动的路线依次为:A→M(+2,+3),M→N(+1,-1),N→P(-2,+2),P→Q
(+4,-4),请你依次在图7-2-2-9②上标出点M,N,P,Q的位置;
(3)在图7-2-2-9②中,若点A经过(m,n)得到点E,点E再经过(p,q)后得到Q,则m
与p满足的数量关系是 ????;n与q满足的数量关系是 ????.
?
图7-2-2-9
解析 (1)1+3+3+|-2|+|-1|+|-4|=14.
(2)如图.
?
(3)m+p=5;n+q=0.
一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移
1个单位.用有理数加法表示为3+(-2)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左
为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}
与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平
移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照
“平移量”{3,1}平移,最后的位置还是点B吗? 在图①中画出四边形
OABC;
(3)如图②,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航
行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航
行过程.
?
解析 (1){3,1}+{1,2}={4,3};
{1,2}+{3,1}={4,3}.
(2)如图,最后的位置仍是B.
?
(3)从O出发到P(2,3),先向右平移2个单位,再向上平移3个单位,可知“平移
量”为{2,3},同理得到从P到Q的“平移量”为{3,2},从Q到O的“平移
量”为{-5,-5},故有{2,3}+{3,2}+{-5,-5}={0,0}.
知识点一????坐标系中点的平移
点P(x,y)的平移方式(a>0,b>0) 平移后点的坐标
点的
平移
方式 左右平移 向右平移a个单位 (x+a,y)
向左平移a个单位 (x-a,y)
上下平移 向上平移b个单位 (x,y+b)
向下平移b个单位 (x,y-b)
如图7-2-2-1(其中a>0).
?
图7-2-2-1
例1 把点M(-3,1)向上平移2个单位得到点N,则点N的坐标为 ????,再
把点N向左平移4个单位得到点Q,则点Q的坐标为 ????.
解析 把点M(-3,1)向上平移2个单位,则横坐标不变,纵坐标加上2,所以N(-
3,3);把点N(-3,3)向左平移4个单位,则纵坐标不变,横坐标减去4,得Q(-7,3).
答案 (-3,3);(-7,3)
知识点二????坐标系中图形的平移
坐标系中图形的平移是指在平面直角坐标系中,保持坐标轴不动,只进
行图形的整体移动.在平移变换中,图形的形状和大小都不变,变的仅仅是
图形的位置.
(1)图形中所有点的纵坐标保持不变,横坐标分别加k.
当k>0时,原图形向右平移k个单位长度;当k<0时,原图形向左平移|k|个单位
长度.
(2)图形中所有点的横坐标保持不变,纵坐标分别加k.
当k>0时,原图形向上平移k个单位长度;当k<0时,原图形向下平移|k|个单位
长度.
重点剖析 (1)图形是由点组成的,图形的平移可转化为点的平移,通过点
的坐标的变化来实现图形的平移.
(2)决定平移的因素:平移的方向和平移的距离.
例2 如图7-2-2-2,正方形ABCD的顶点坐标分别为A(1,1),B(3,1),C(3,3),D
(1,3).
(1)在同一直角坐标系中,将正方形ABCD向左平移2个单位,画出相应的图
形,并写出各顶点的坐标;
(2)将正方形ABCD向下平移2个单位,画出相应的图形,并写出各顶点的坐
标;
(3)在(1)(2)中,你发现各点的横、纵坐标发生了哪些变化?
?
图7-2-2-2
解析 (1)在同一直角坐标系中,将正方形ABCD向左平移2个单位,得到如
图7-2-2-3中的正方形A'B'C'D'.正方形A'B'C'D'的各顶点坐标为A'(-1,1),B'(1,
1),C'(1,3),D'(-1,3).
?
图7-2-2-3
(2)在同一直角坐标系中,将正方形ABCD向下平移2个单位,得到如图7-2-2-
3中的正方形A″B″C″D″.正方形A″B″C″D″的各顶点坐标为A″
(1,-1),B″(3,-1),C″(3,1),D″(1,1).
(3)在(1)中,各点的纵坐标不变,横坐标都减小2;在(2)中,各点的横坐标不变,
纵坐标都减小2.
点拨????对一个图形进行平移,这个图形上所有点的坐标都发生相同的变化,
即图形的平移也就是把图形上的点进行平移.因此,掌握好点的坐标的平移
规律是解决此类问题的关键.
题型一????图形的平移与坐标变化
例1 如图7-2-2-4,在平面直角坐标系中,△ABC的顶点都在方格纸的格点
上,如果将△ABC先向右平移4个单位长度,再向下平移1个单位长度,得到
△A1B1C1,那么点A的对应点A1的坐标为?( )
?
图7-2-2-4
A.(4,3) ????B.(2,4) ????C.(3,1) ????D.(2,5)
解析 由坐标系可得A(-2,6),将△ABC先向右平移4个单位长度,再向下平
移1个单位长度,点A的对应点A1的坐标为(-2+4,6-1),即(2,5),如图7-2-2-5所
示.
?
图7-2-2-5
答案????D
点拨 首先寻找到图形的平移规律,再根据“图形平移时,图形上每一点的
平移规律与该图形的平移规律保持一致”求解.
题型二????平移作图
例2 如图7-2-2-6,将△ABC向右平移4个单位长度,再向下平移5个单位长
度.
(1)作出平移后的△A'B'C';
(2)求出△A'B'C'的面积.
?
图7-2-2-6
解析 (1)如图7-2-2-7.
?
图7-2-2-7
(2)△A'B'C'的面积是7×8-?×3×7-?×5×2-?×8×5=20.5.
棋盘上的数学
典例剖析????
例 下象棋是很多人喜爱的事,你知道象棋里充满着数学问题吗?如图7-2-
2-8,象棋的棋盘上有一个马,它跳七步能回到原来的位置上吗?若能,请给出
一种跳法;若不能,请说明理由.
?
图7-2-2-8
素养呈现 逻辑推理是指从一些事实和命题出发,依据逻辑规则推出其他
命题的素养.主要包括两类:一类是从特殊到一般的推理,推理形式主要有
归纳、类比;一类是从一般到特殊的推理,推理形式主要有演绎.本题以下
象棋为背景,通过逻辑推理来说明马跳七步不可能回到原来的位置.
解析 无论怎么跳,马都不能回到原来的位置,理由如下:
如图7-2-2-9,我们可在棋盘上建立直角坐标系,并设这个马所在的位置P的
坐标为(x0,y0),那么,马跳一步后的位置的坐标应为(x0+x1,y0+y1),这里的x1和y1
只可能分别是1,-1,2,-2这四个数中的一个(想一想,为什么).
同样,跳第二步后,马所在的位置的坐标应为(x0+x1+x2,y0+y1+y2),这里的x2和y2
也只可能是1,-1,2,-2中的一个,依此类推,跳七步后,马所在的位置的坐标为
(x0+x1+x2+x3+x4+x5+x6+x7,y0+y1+y2+y3+y4+y5+y6+y7),如果这时马又回到原来的
位置(x0,y0),那么有x0+x1+x2+x3+x4+x5+x6+x7=x0,y0+y1+y2+y3+y4+y5+y6+y7=y0,也即
x1+x2+x3+x4+x5+x6+x7=0,y1+y2+y3+y4+y5+y6+y7=0,
将两式相加,有(x1+y1)+(x2+y2)+(x3+y3)+(x4+y4)+(x5+y5)+(x6+y6)+(x7+y7)=0.
上式中14个数只能分别取1,-1,2,-2中的一个,根据象棋中“马”跳一步的
规则可知x1+y1,x2+y2,x3+y3,x4+y4,x5+y5,x6+y6,x7+x7这七个数只能分别取1,-1,3,-3
中的一个,但是无论怎样取,由于奇数个奇数相加的和为奇数,所以这样取
出的七个数的和不可能等于0,故马跳七步不可能回到原来的位置.
?
图7-2-2-9
素养解读 逻辑推理是得到数学结论、构建数学体系的重要方式,是数学
严谨性的基本保证,是人们在数学活动中进行交流的基本思维品质.在逻辑
推理核心素养的形成过程中,学生能够发现问题和提出命题;能掌握推理的
基本形式,探索和表述论证过程;能理解数学知识之间的联系,建构知识框
架,形成有论据、有条理、合乎逻辑的思维品质,增强数学交流能力.
知识点一????坐标系中点的平移
1.已知点A(-2,4),将点A往上平移2个单位长度,再往左平移3个单位长度得
到点A',则点A'的坐标是?( )
A.(-5,6) ????B.(1,2) ????C.(1,6) ????D.(-5,2)
答案????A????点A往上平移2个单位长度,再往左平移3个单位长度后,点的坐
标为(-2-3,4+2),即A'(-5,6),故选A.
2.(独家原创试题)在平面直角坐标系中,将点P(-3,4)平移至原点,则平移方
式可以是?( )
A.先向左平移3个单位长度,再向上平移4个单位长度
B.先向右平移4个单位长度,再向上平移3个单位长度
C.先向左平移3个单位长度,再向下平移4个单位长度
D.先向右平移3个单位长度,再向下平移4个单位长度
答案????D 将点P(-3,4)的横坐标加3,纵坐标减4可平移至原点(0,0),故可以
先向右平移3个单位长度,再向下平移4个单位长度.
知识点二????坐标系中图形的平移
3.已知△ABC在平面直角坐标系中的位置如图7-2-2-1所示,将△ABC先向
下平移5个单位,再向左平移2个单位,则平移后C点的坐标是?( )
?
图7-2-2-1
A.(5,-2) ????B.(1,-2) ????C.(2,-1) ????D.(2,-2)
答案????B ∵△ABC先向下平移5个单位,再向左平移2个单位,∴平移后点
C的横坐标为3-2=1,纵坐标为3-5=-2,∴平移后点C的坐标为(1,-2).故选B.
4.(独家原创试题)平面直角坐标系中,A(2,1),B(4,1),将线段AB平移,使得AB
的中点落在对应点(-1,-2)的位置,则点A的对应点的坐标为 ????.
答案 (-2,-2)
解析 由A(2,1),B(4,1)可知AB∥y轴,易知AB的中点坐标为(3,1),由(3,1)平
移到(-1,-2),可知横坐标减4,纵坐标减3,故点A的对应点为(2-4,1-3),即(-2,-
2).
5.如图7-2-2-2,方格纸中每个小方格都是边长为1个单位长度的正方形,在
平面直角坐标系中,已知点A(1,0),B(4,0),C(3,3),D(1,4).
(1)描出A、B、C、D四点的位置,并顺次连接A、B、C、D、A;
(2)四边形ABCD的面积是 ????;
(3)把四边形ABCD向左平移5个单位,再向上平移1个单位得到四边形A'B'C'
D',在图中画出四边形A'B'C'D',并写出A'、B'、C'、D'的坐标.
?
图7-2-2-2
解析 (1)如图.
?
(2)四边形ABCD的面积是?.
(3)四边形A'B'C'D'如图.其中A'(-4,1)、B'(-1,1)、C'(-2,4)、D'(-4,5).
1.(2018湖北黄石中考)如图,将“笑脸”图标向右平移4个单位,再向下平移
2个单位,点P的对应点P'的坐标是?( )
A.(-1,6) ????B.(-9,6) ????
C.(-1,2) ????D.(-9,2)
答案????C????由题图知P(-5,4),向右平移4个单位,再向下平移2个单位,点P的
对应点P'的坐标是(-1,2),故选C.
2.将点P(m+2,2m+4)向右平移1个单位到P',且P'在y轴上,那么P'的坐标是?
( )
A.(-2,0) ????B.(0,-2) ????C.(1,0) ????D.(0,1)
答案????B????点P(m+2,2m+4)向右平移1个单位后的坐标为(m+3,2m+4),所以P
'(m+3,2m+4),由于该点在y轴上,所以m+3=0,m=-3,所以2m+4=-2.所以P'(0,-
2).
3.点M(4,3)向 ????(填“上”“下”“左”或“右”)平移 ????个
单位后落在y轴上;向 ????(填“上”“下”“左”或“右”)平移 ????
????个单位后落在x轴上.
答案 左;4;下;3
解析 根据点的坐标的平移规律,点M(4,3)要平移至y轴上,则横坐标要减4,
故向左平移4个单位;点M(4,3)要平移至x轴上,则纵坐标要减3,故向下平移3
个单位.
4.(2016黑龙江哈尔滨双城期末)在同一坐标系中,图形a是由图形b向上平
移3个单位长度得到的,如果图形a中点A的坐标为(4,-2),则图形b中与点A对
应的点A'的坐标为 ????.
答案 (4,1)
解析 图形向上平移3个单位长度,图形中的点的坐标的变化是横坐标不
变,纵坐标加上3.
5.(2017广东深圳一模)如图,直角坐标系中,△ABC的顶点都在网格点上,其
中C点坐标为(1,2).(8分)
(1)点A的坐标是 ????,点B的坐标是 ????;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'
C',画出△A'B'C',并写出△A'B'C'的三个顶点的坐标;
(3)求△ABC的面积.
解析 (1)(2,-1);(4,3).
(2)画出的△A'B'C'如图所示;A'(0,0),B'(2,4),C'(-1,3).
?
(3)△ABC的面积=3×4-?×2×4-?×3×1-?×3×1=5.
1.(2016山东青岛中考)如图7-2-2-3,线段AB经过平移得到线段A'B',其中
点A,B的对应点分别为点A',B',这四个点都在格点上.若线段AB上有一个点
P(a,b),则点P在A'B'上的对应点P'的坐标为?( )
?
图7-2-2-3
A.(a-2,b+3) ????B.(a-2,b-3)
C.(a+2,b+3) ????D.(a+2,b-3)
答案????A????由题图可知线段AB向左平移2个长度单位,再向上平移3个长度
单位得到线段A'B',由此可知线段AB上的点P(a,b)的对应点P'的坐标为(a-2,
b+3),故选A.
2.如图7-2-2-4所示,四边形ABCO中,AB∥OC,BC∥AO,A、C两点的坐标分
别为(-?,?)、(-2?,0),A、B两点间的距离等于O、C两点间的距离.
(1)点B的坐标为 ????;
(2)将这个四边形向下平移2?个单位长度后得到四边形A'B'C'O',请你写出
平移后四边形四个顶点的坐标.
图7-2-2-4
解析 (1)∵C点的坐标为(-2?,0),∴OC=2?.
∵AB∥OC,AB=OC,∴将A点向左平移2?个单位得到B点,又∵A点的坐标
为(-?,?),
∴B点的坐标为(-?-2?,?),即(-3?,?).
(2)∵将四边形ABCO向下平移2?个单位长度后得到四边形A'B'C'O',∴A'
点的坐标为(-?,-?),B'点的坐标为(-3?,-?),C'点的坐标为(-2?,-2?),
O'点的坐标为(0,-2?).
1.(2019福建厦门模拟)在平面直角坐标系xOy中,点P(0,1)第1次向右平移1
个单位长度,向下平移2个单位长度至点P1(1,-1);第2次向右平移1个单位长
度,向上平移3个单位长度至点P2(2,2);第3次向右平移1个单位长度,向下平
移4个单位长度至点P3(3,-2);第4次向右平移1个单位长度,向上平移5个单
位长度至点P4(4,3),……,按照此规律,点P2 019的坐标是?( )
A.(2 019,1 009) ????B.(2 019,-1 009)
C.(2 019,1 010) ????D.(2 019,-1 010)
答案????D 根据题意,可知点P第n次移动的规律是:向右平移1个单位长度,
向上或向下平移(n+1)个单位长度,其中n为奇数时向下,n为偶数时向上.因
此,点P第2 019次平移至点P2 019的横坐标是0+1×2 019=2 019,纵坐标是1-2+
3-4+5-6+7-…+2 019-2 020=-1 010,
即点P2 019的坐标是(2 019,-1 010).
2.如图,△A'B'C'是由△ABC经过某种变换后得到的图形,如果△ABC中有一
点P的坐标为(a,2),那么变换后它的对应点Q的坐标为 ????.
?
答案 (a+5,-2)
解析 由题图可知,A(-4,3),A'(1,-1),由点A向右平移5个单位,向下平移4个
单位可得点A',
故P(a,2)的对应点Q的坐标为(a+5,-2).
3.如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点
的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速
度沿着O→A→B→C→O的路线移动.
(1)点B的坐标为 ????;
(2)当点P移动了4秒时,求出点P的坐标;
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
解析 (1)根据长方形的性质,可得AB与y轴平行,BC与x轴平行,故点B的坐
标为(4,6).
(2)∵P的运动速度为每秒2个单位长度,∴当点P移动了4秒时,共运动了8个
单位长度,此时点P位于AB上,且坐标为(4,4).
(3)当P在AB上时,P运动了4+5=9个单位长度,此时点P运动了9÷2=4.5秒;
当P在OC上时,P运动了4+6+4+1=15个单位长度,此时点P运动了15÷2=7.5
秒.
一、选择题
1.(2019天津和平期末,8,★☆☆)在平面直角坐标系中,将点P先向左平移2
个单位长度,再向下平移3个单位长度后的对应点的坐标为(-1,3),则点P的
坐标为?( )
A.(2,3) ????B.(-2,-3) ????C.(2,5) ????D.(1,6)
答案????D 设点P的坐标为(x,y),则有x-2=-1,y-3=3,得x=1,y=6,所以点P的坐
标为(1,6).
2.(2019安徽合肥庐江期末,10,★★☆)如图7-2-2-5,点A1(1,1),点A1向上平移
1个单位,再向右平移2个单位,得到点A2;点A2向上平移2个单位,再向右平移
4个单位,得到点A3;点A3向上平移4个单位,再向右平移8个单位,得到点A4,…
…,按这个规律平移得到点An,则点An的横坐标为?( )
?
图7-2-2-5
A.2n ????B.2n-1 ????C.2n-1 ????D.2n+1
答案????C 由题意知,点A1的横坐标为1=21-1,点A2的横坐标为3=22-1,点A3的
横坐标为7=23-1,点A4的横坐标为15=24-1,……,按这个规律平移得到点An的
横坐标为2n-1.
二、填空题
3.(2018湖北天门模拟,13,★★☆)如图7-2-2-6,点A、B的坐标分别为(1,2)、
(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为 ????
????.
?
图7-2-2-6
答案 (4,2)
解析 易知OD=3,即△AOB沿x轴向右平移3个单位长度得到△CDE,∴点
C的坐标为(4,2).
4.(2017江西景德镇二中期末,10,★★☆)在平面直角坐标系中,△A'B'C'是
由△ABC平移得到的,△ABC中任意一点P(x0,y0)经过平移后的对应点为P'(x
0+7,y0+2),若A'的坐标为(5,3),则它的对应点A的坐标为 ????.
答案 (-2,1)
解析 根据题意,可得△ABC到△A'B'C'的平移规律为向右平移7个单位,向
上平移2个单位,∵A'的坐标为(5,3),∴它的对应点A的坐标为(-2,1).
1.(2018安徽合肥六中期末,3,★☆☆)在平面直角坐标系中,点A'(2,-3)可以
由点A(-2,3)通过两次平移得到,则下列说法正确的是?( )
A.先向左平移4个单位长度,再向上平移6个单位长度
B.先向右平移4个单位长度,再向上平移6个单位长度
C.先向左平移4个单位长度,再向下平移6个单位长度
D.先向右平移4个单位长度,再向下平移6个单位长度
答案????D 把点A(-2,3)先向右平移4个单位长度,再向下平移6个单位长度
得到点A'(2,-3).故选D.
2.(2019四川广安期末,7,★★☆)△ABC所在平面内任意一点P(a,b)经过平
移后的对应点为P1(c,d),已知A(2,3)经过此次平移后的对应点为A1(5,-1),则a
+b-c-d的值为?( )
A.-5 ????B.5
C.-1 ????D.1
答案????D 由A(2,3)先向右平移3个单位长度,再向下平移4个单位长度可得
A1(5,-1),所以c=a+3,d=b-4,即a-c=-3,b-d=4,则a+b-c-d=-3+4=1.
3.(2019广东广州番禺二中期中,10,★★☆)如图,在平面直角坐标系中,点P
(1,0)第1次向上跳动1个单位至点P1(1,1),第2次向左跳动2个单位至点P2(-1,
1),第3次向上跳动1个单位至点P3(-1,2),第4次向右跳动3个单位至点P4(2,2),
第5次又向上跳动1个单位至点P5(2,3),……,依此规律跳动下去,点P200的坐
标是?( )
?
A.(51,100) ????B.(50,100) C.(-50,100) ????D.(-51,100)
答案????A 由题中规律可知P200的坐标与P4(2,2),P8(3,4),P12(4,6),……,P4n(n+
1,2n)的规律一致,而200÷4=50,故P200的坐标为(50+1,2×50),即(51,100).
4.(2019四川南充嘉陵二中月考,25,★★★)如图,在平面直角坐标系中,同时
将点A(-1,0)、B(3,0)向上平移2个单位长度,再向右平移1个单位长度,分别
得到A、B的对应点C、D.连接AC,BD.
(1)求点C、D的坐标,并描出点A、B、C、D,求四边形ABDC面积;
(2)在坐标轴上是否存在点P,连接PA、PC,使S△PAC=S四边形ABDC?若存在,求出点
P的坐标;若不存在,请说明理由.
解析 (1)点C的坐标为(-1+1,0+2),即(0,2),点D的坐标为(3+1,0+2),即(4,2),
如图所示,根据平移的性质,可知四边形ABDC为平行四边形,则S四边形ABDC=2×
4=8.
?
(2)存在.当P在x轴上时,∵S△PAC=S四边形ABDC,
∴?AP·OC=8,∵OC=2,∴AP=8,
∴点P的坐标为(7,0)或(-9,0);
当P在y轴上时,∵S△PAC=S四边形ABDC,
∴?CP·OA=8,∵OA=1,∴CP=16,
∴点P的坐标为(0,18)或(0,-14).
综上,点P的坐标为(7,0)或(-9,0)或(0,18)或(0,-14).
一、选择题
1.(2019辽宁大连中考,4,★☆☆)在平面直角坐标系中,将点P(3,1)向下平移
2个单位长度,得到的点P'的坐标为?( )
A.(3,-1) ????B.(3,3) ????C.(1,1) ????D.(5,1)
答案????A 将点P(3,1)向下平移2个单位长度,得到的点P'的坐标为(3,1-2),
即(3,-1).
2.(2019海南中考,8,★☆☆)如图7-2-2-7,在平面直角坐标系中,已知点A(2,
1),点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标
为?( )
?
图7-2-2-7
A.(-1,-1) ????B.(1,0) ????C.(-1,0) ????D.(3,0)
答案????C ∵将点A(2,1)向左平移4个单位,向上平移1个单位可得点A1(-2,
2),∴点B的对应点B1的坐标为(3-4,-1+1),即(-1,0).
3.(2019甘肃兰州中考,10,★☆☆)如图7-2-2-8,在平面直角坐标系xOy中,将
四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(-3,5),B(-
4,3),A1(3,3),则点B1的坐标为?( )
?
图7-2-2-8
A.(1,2) ????B.(2,1)
C.(1,4) ????D.(4,1)
答案????B ∵3=-3+6,3=5-2,∴四边形ABCD先向下平移2个单位长度,再向
右平移6个单位长度,∴B1的坐标是(2,1),故选B.
二、填空题
4.(2018江苏宿迁中考,14,★☆☆)在平面直角坐标系中,将点(3,-2)先向右平
移2个单位长度,再向上平移3个单位长度,则所得点的坐标是 ????.
答案 (5,1)
解析 将点(3,-2)先向右平移2个单位长度,
得到点(5,-2),再向上平移3个单位长度,
所得点的坐标是(5,1).
1.(2019四川成都中考,4,★☆☆)在平面直角坐标系中,将点(-2,3)向右平移4
个单位长度后得到的点的坐标为?( )
A.(2,3) ????B.(-6,3)
C.(-2,7) ????D.(-2,-1)
答案????A 将点(-2,3)向右平移4个单位长度得到的点的坐标为(-2+4,3),即
(2,3).
2.(2017湖南邵阳中考,10,★☆☆)如图,三架飞机 P,Q,R 保持编队飞行,某时
刻在坐标系中的坐标分别为(-1,1),(-3,1),(-1,-1).30 秒后,飞机 P 飞到 P'(4,3)
的位置,则飞机 Q,R 的位置Q',R'分别为?( )
?
A.Q'(2,3),R'(4,1) ????B.Q'(2,3),R'(2,1)
C.Q'(2,2),R'(4,1) ????D.Q'(3,3),R'(3,1)
答案????A????因为保持编队飞行,且点(-1,1)移动到P'(4,3)向右平移了5个单
位,向上平移了2个单位,所以点(-3,1),(-1,-1)平移后的坐标分别为(2,3),(4,1),
故选A.
3.(2017辽宁大连中考,7,★☆☆)在平面直角坐标系xOy中,线段AB的两个端
点坐标分别为A(-1,-1),B(1,2).平移线段AB,得到线段A'B'.已知点A'的坐标为
(3,-1),则点B'的坐标为?( )
A.(4,2) ????B.(5,2) ????C.(6,2) ????D.(5,3)
答案????B 由于A(-1,-1),A'(3,-1),说明线段AB向右平移了4个单位,因此B点
也相应地向右平移了4个单位,因此B'(5,2).故选B.
4.(2017广西百色中考,16,★★☆)如图,在正方形OABC中,O为坐标原点,点
C在y轴正半轴上,点A的坐标为(2,0),将正方形OABC沿着OB方向平移?OB
个单位,则点C的对应点的坐标是 ????.
?
答案 (1,3)
解析 易知OC=OA=2,所以C(0,2),将正方形OABC沿着OB方向平移?OB个
单位,即将正方形OABC先向右平移1个单位,再向上平移1个单位,故点C的
对应点的坐标是(1,3).
5.(2015山东青岛中考,10,★☆☆)如图,将平面直角坐标系中“鱼”的每个
“顶点”的纵坐标保持不变,横坐标分别变为原来的?,那么点A的对应点A
'的坐标是 ????.
?
答案 (2,3)
解析 由题图可知,点A变化前的坐标为(6,3),将纵坐标保持不变,横坐标变
为原来的?,则点A的对应点A'的坐标是(2,3).
在由边长为1的小正方形组成的网格中,把一个点先沿水平方向平移|a|
格(当a为正数时,表示向右平移;当a为负数时,表示向左平移),再沿竖直方
向平移|b|格(当b为正数时,表示向上平移;当b为负数时,表示向下平移),得
到一个新的点,我们把这个过程记为(a,b),例如在图7-2-2-9①中,从A到B记
为:A→B(+1,+3);从C到D记为:C→D(+1,-3).
请回答下列问题:
(1)如图7-2-2-9①,若点A的运动路线为:A→B→D→A,请计算点A运动的总
路程;
(2)若点A运动的路线依次为:A→M(+2,+3),M→N(+1,-1),N→P(-2,+2),P→Q
(+4,-4),请你依次在图7-2-2-9②上标出点M,N,P,Q的位置;
(3)在图7-2-2-9②中,若点A经过(m,n)得到点E,点E再经过(p,q)后得到Q,则m
与p满足的数量关系是 ????;n与q满足的数量关系是 ????.
?
图7-2-2-9
解析 (1)1+3+3+|-2|+|-1|+|-4|=14.
(2)如图.
?
(3)m+p=5;n+q=0.
一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移
1个单位.用有理数加法表示为3+(-2)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左
为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}
与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平
移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照
“平移量”{3,1}平移,最后的位置还是点B吗? 在图①中画出四边形
OABC;
(3)如图②,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航
行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航
行过程.
?
解析 (1){3,1}+{1,2}={4,3};
{1,2}+{3,1}={4,3}.
(2)如图,最后的位置仍是B.
?
(3)从O出发到P(2,3),先向右平移2个单位,再向上平移3个单位,可知“平移
量”为{2,3},同理得到从P到Q的“平移量”为{3,2},从Q到O的“平移
量”为{-5,-5},故有{2,3}+{3,2}+{-5,-5}={0,0}.
