华东师大版数学八年级上册14.2勾股定理的应用 (共25张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册14.2勾股定理的应用 (共25张PPT) | 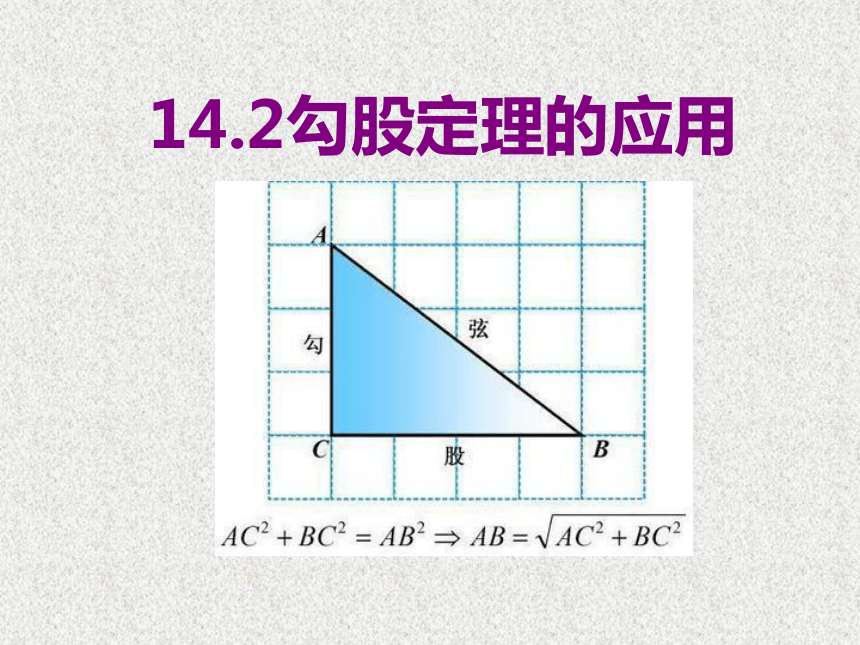 | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 09:07:07 | ||
图片预览





文档简介
(共25张PPT)
14.2勾股定理的应用
圆柱体表面上两点间的最短距离
正方体或长方体表面上两点间的最短距离
勾股定理的其他应用
1
知识点
圆柱体表面上两点间的最短距离
(1)在平面上寻找两点之间的最短路线的依据:①两点之间线段
最短;②直线外一点到直线上所有点的连线中,垂线段最短.
(2)在立体图形中,由于受到物体和空间的阻隔,两点间的最短
路线长不一定是两点间的线段长.
(3)确定立体图形上的最短路线,需要先将立体图形展开成平面
图形,再构造直角三角形进行计算,最后通过比较得出最短
路线.
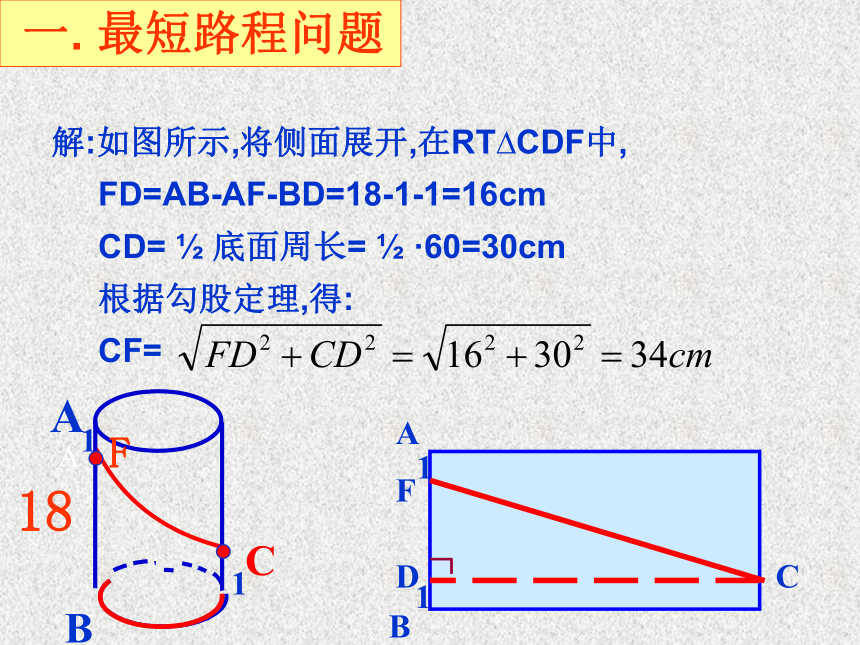
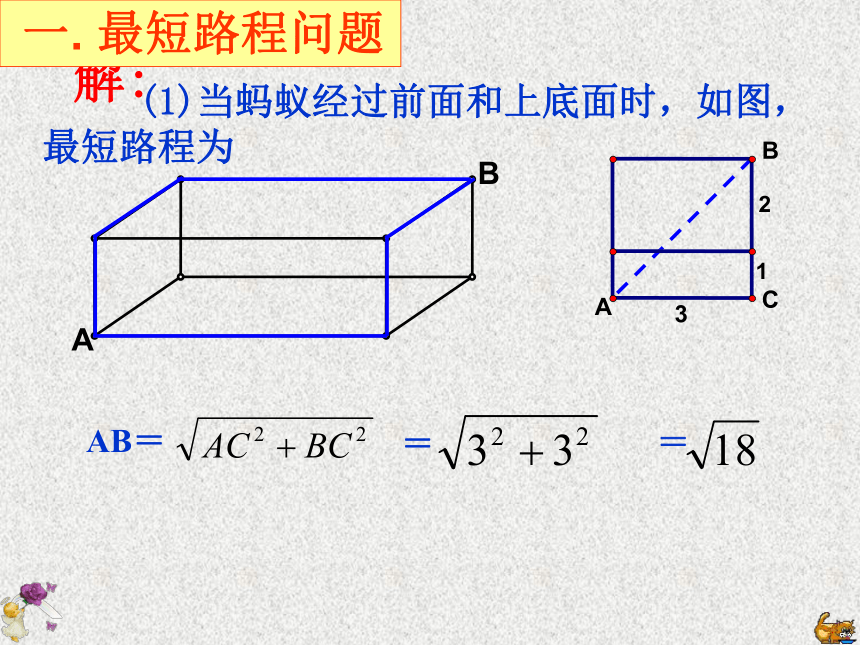
一. 最短路程问题
一. 最短路程问题
1
1
2
知识点
正方体或长方体表面上两点间的最短距离
求长方体(或正方体)表面上两点间的最短路线长的
方法:
先将长方体(或正方体)的表面展开成平面图形,
展开时一般要考虑各种可能的情况.在各种可能的
情况中,分别确定两点的位置并连结成线段,再利
用勾股定理分别求其长度,最后进行比较,长度最
短的路线为最短路线.
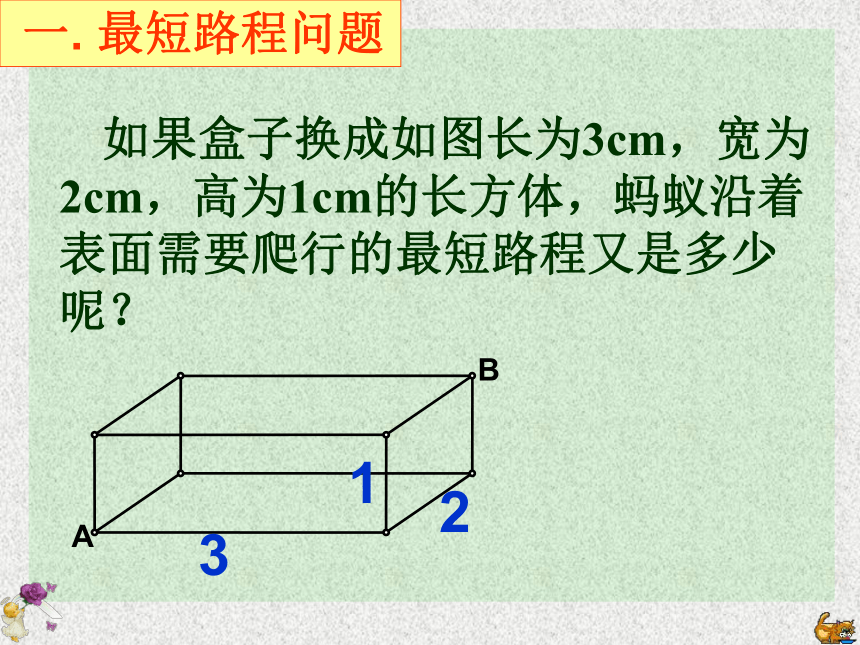
一. 最短路程问题
如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
3
2
1
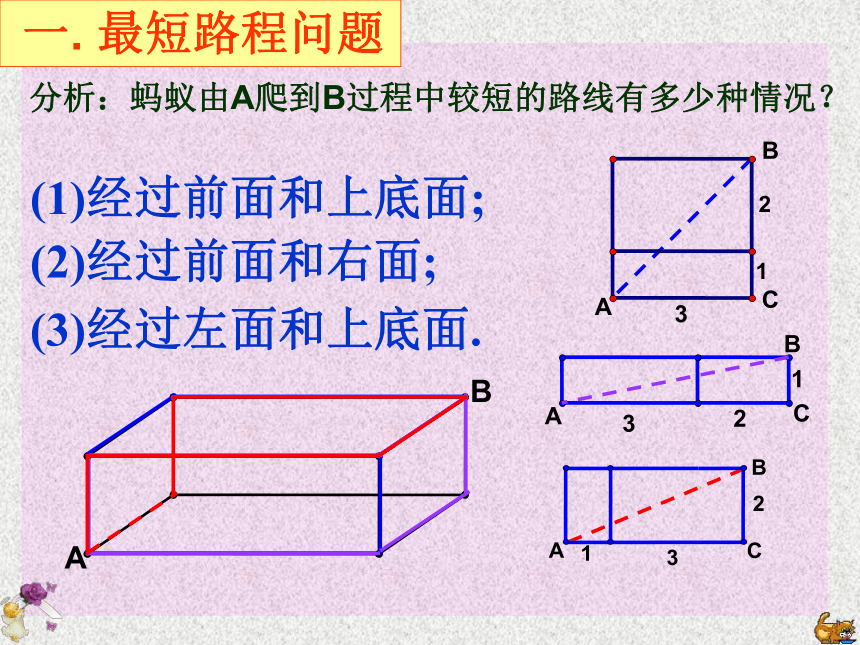
一. 最短路程问题
分析:蚂蚁由A爬到B过程中较短的路线有多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
一. 最短路程问题
(1)当蚂蚁经过前面和上底面时,如图,最短路程为
解:
AB=
=
=
一. 最短路程问题
(2)当蚂蚁经过前面和右面时,如图,最短路程为
AB=
=
=
一. 最短路程问题
(3)当蚂蚁经过左面和上底面时,如图,最短路程为
AB=
=
=
最短路程为 ㎝
一. 最短路程问题
解决有关立体图形中路线最短的问题,其关键是
把立体图形中的路线问题转化为平面上的路线问题.
如圆柱侧面展开图为长方形,圆锥侧面展开图为扇形,
长方体侧面展开图为长方形等.运用平面上两点间线
段最短的道理,利用勾股定理求解.
一. 最短路程问题
3
知识点
勾股定理的其他应用
1.在一些求高度、宽度、长度、距离等量的问题中,
首先要结合题意画出符合要求的直角三角形,也就
是把实际问题转化为数学问题,进而把要求的量看
成直角三角形的一条边,然后利用勾股定理进行求
解.
2.在日常生活中,判断一个角是否为直角时,除了
用三角板、量角器等测量角度的工具外,还可以
通过测量长度,结合勾股定理的逆定理来判断.
二.勾股定理的其他应用
轴对称问题
如图所示,一牧童在A处放羊,他家在B处,A、B两处相距河岸的距离AC、BD分别为500m和700m,且CD=500m,天黑前牧童从A处将羊牵到河边饮水后再赶回家,请通过计算说明牧童至少要走多少米?
A
F
E
D
C
B
P
解:作点A关于CD对称的点E,连结BE,交CD于点P,连结AP,则沿着AP、PB回家的路程最短.
过点E作EF垂直于BD交BD的延长线于点F.
两点之间线段最短
二.勾股定理的其他应用
轴对称问题
如图所示,正方形ABCD的边长为8cm,点M在AB上,BM=2cm,对角线AC上有一动点P,求PM+PB的最小值.
D
解:连结BD,连结DM交AC于点P,连结PB,则PM+PB的最小值就是DM的长度.
两点之间线段最短
A
B
C
·
M
·
P
二.勾股定理的其他应用
网格问题
(2)
(1)
(3)
已知如图所示,正方形的边长都是1,如图(1)所示,可以算出正方形的对角线长为 ,那么两个正方形并排所构成的矩形的对角线长为 ,n个正方形并排所得矩形的对角线为 .
(4)
二.勾股定理的其他应用
网格问题
A
B
C
在网格中画线段时,把线段看作是某些正方形或长方形的边或对角线
二.勾股定理的其他应用
网格问题
A
B
C
如图,长方形网格中,每个小正方形的边长为1,以AB为边画△ABC,使BC长为无理数,
AC长为有理数.
5
5
C′
二.勾股定理的其他应用
如图,小方格都是边长为1的正方形,
求四边形ABCD的面积.
网格问题
二.勾股定理的其他应用
如图所示,在?ABC中,AB=AC,点D在CB延长线上,试说明:AD?-AB?=BD·CD
∟
A
B
C
D
含有平方的等式问题
E
在RT?ADE和RT?AEC中,
根据勾股定理得,
AD?=AE?+DE?, AC?=AE?+EC?
∵AB=AC AE⊥BC
∴EB=EC
∴AD?-AB?=DE?-EC?
=(DE-EC)·(DE+EC)
=(DE-EB)·DC
=BD·DC
即AD?-AB?=BD·CD
解: 作高AE
二.勾股定理的其他应用
1、 有一块田地的形状和尺寸如图所示,试求它的面积。
∟
∟
A
B
C
D
5
面积问题
13
12
二.勾股定理的其他应用
2.如图,在四边形ABCD中,∠B=900 AB=BC=4,CD=6,AD=2,求四边形ABCD的面积。
面积问题
6
2
4
4
二.勾股定理的其他应用
折叠问题
1、矩形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,折痕是EF,求DE的长度?
A
B
C
D
E
F
(B)
(C)
二.勾股定理的其他应用
折叠问题
2、如图,在矩形ABCD中,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,AB=8cm,CE=3cm,求BF的长度。
二.勾股定理的其他应用
3、如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
折叠问题
二.勾股定理的其他应用
应用勾股定理解决实际问题的一般思路:将实际
问题转化为数学模型,然后利用勾股定理列出方程,
再解方程求解.由于勾股定理反映了直角三角形三边
之间的关系,因此往往与方程进行联系.即应用时要
注意两点:(1)在解决实际问题时,注意从“形”到
“数”的转化;(2)在解决实际问题时,注意构造直角
三角形模型,结合方程进行求解.
14.2勾股定理的应用
圆柱体表面上两点间的最短距离
正方体或长方体表面上两点间的最短距离
勾股定理的其他应用
1
知识点
圆柱体表面上两点间的最短距离
(1)在平面上寻找两点之间的最短路线的依据:①两点之间线段
最短;②直线外一点到直线上所有点的连线中,垂线段最短.
(2)在立体图形中,由于受到物体和空间的阻隔,两点间的最短
路线长不一定是两点间的线段长.
(3)确定立体图形上的最短路线,需要先将立体图形展开成平面
图形,再构造直角三角形进行计算,最后通过比较得出最短
路线.
一. 最短路程问题
一. 最短路程问题
1
1
2
知识点
正方体或长方体表面上两点间的最短距离
求长方体(或正方体)表面上两点间的最短路线长的
方法:
先将长方体(或正方体)的表面展开成平面图形,
展开时一般要考虑各种可能的情况.在各种可能的
情况中,分别确定两点的位置并连结成线段,再利
用勾股定理分别求其长度,最后进行比较,长度最
短的路线为最短路线.
一. 最短路程问题
如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
3
2
1
一. 最短路程问题
分析:蚂蚁由A爬到B过程中较短的路线有多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
一. 最短路程问题
(1)当蚂蚁经过前面和上底面时,如图,最短路程为
解:
AB=
=
=
一. 最短路程问题
(2)当蚂蚁经过前面和右面时,如图,最短路程为
AB=
=
=
一. 最短路程问题
(3)当蚂蚁经过左面和上底面时,如图,最短路程为
AB=
=
=
最短路程为 ㎝
一. 最短路程问题
解决有关立体图形中路线最短的问题,其关键是
把立体图形中的路线问题转化为平面上的路线问题.
如圆柱侧面展开图为长方形,圆锥侧面展开图为扇形,
长方体侧面展开图为长方形等.运用平面上两点间线
段最短的道理,利用勾股定理求解.
一. 最短路程问题
3
知识点
勾股定理的其他应用
1.在一些求高度、宽度、长度、距离等量的问题中,
首先要结合题意画出符合要求的直角三角形,也就
是把实际问题转化为数学问题,进而把要求的量看
成直角三角形的一条边,然后利用勾股定理进行求
解.
2.在日常生活中,判断一个角是否为直角时,除了
用三角板、量角器等测量角度的工具外,还可以
通过测量长度,结合勾股定理的逆定理来判断.
二.勾股定理的其他应用
轴对称问题
如图所示,一牧童在A处放羊,他家在B处,A、B两处相距河岸的距离AC、BD分别为500m和700m,且CD=500m,天黑前牧童从A处将羊牵到河边饮水后再赶回家,请通过计算说明牧童至少要走多少米?
A
F
E
D
C
B
P
解:作点A关于CD对称的点E,连结BE,交CD于点P,连结AP,则沿着AP、PB回家的路程最短.
过点E作EF垂直于BD交BD的延长线于点F.
两点之间线段最短
二.勾股定理的其他应用
轴对称问题
如图所示,正方形ABCD的边长为8cm,点M在AB上,BM=2cm,对角线AC上有一动点P,求PM+PB的最小值.
D
解:连结BD,连结DM交AC于点P,连结PB,则PM+PB的最小值就是DM的长度.
两点之间线段最短
A
B
C
·
M
·
P
二.勾股定理的其他应用
网格问题
(2)
(1)
(3)
已知如图所示,正方形的边长都是1,如图(1)所示,可以算出正方形的对角线长为 ,那么两个正方形并排所构成的矩形的对角线长为 ,n个正方形并排所得矩形的对角线为 .
(4)
二.勾股定理的其他应用
网格问题
A
B
C
在网格中画线段时,把线段看作是某些正方形或长方形的边或对角线
二.勾股定理的其他应用
网格问题
A
B
C
如图,长方形网格中,每个小正方形的边长为1,以AB为边画△ABC,使BC长为无理数,
AC长为有理数.
5
5
C′
二.勾股定理的其他应用
如图,小方格都是边长为1的正方形,
求四边形ABCD的面积.
网格问题
二.勾股定理的其他应用
如图所示,在?ABC中,AB=AC,点D在CB延长线上,试说明:AD?-AB?=BD·CD
∟
A
B
C
D
含有平方的等式问题
E
在RT?ADE和RT?AEC中,
根据勾股定理得,
AD?=AE?+DE?, AC?=AE?+EC?
∵AB=AC AE⊥BC
∴EB=EC
∴AD?-AB?=DE?-EC?
=(DE-EC)·(DE+EC)
=(DE-EB)·DC
=BD·DC
即AD?-AB?=BD·CD
解: 作高AE
二.勾股定理的其他应用
1、 有一块田地的形状和尺寸如图所示,试求它的面积。
∟
∟
A
B
C
D
5
面积问题
13
12
二.勾股定理的其他应用
2.如图,在四边形ABCD中,∠B=900 AB=BC=4,CD=6,AD=2,求四边形ABCD的面积。
面积问题
6
2
4
4
二.勾股定理的其他应用
折叠问题
1、矩形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,折痕是EF,求DE的长度?
A
B
C
D
E
F
(B)
(C)
二.勾股定理的其他应用
折叠问题
2、如图,在矩形ABCD中,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,AB=8cm,CE=3cm,求BF的长度。
二.勾股定理的其他应用
3、如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
折叠问题
二.勾股定理的其他应用
应用勾股定理解决实际问题的一般思路:将实际
问题转化为数学模型,然后利用勾股定理列出方程,
再解方程求解.由于勾股定理反映了直角三角形三边
之间的关系,因此往往与方程进行联系.即应用时要
注意两点:(1)在解决实际问题时,注意从“形”到
“数”的转化;(2)在解决实际问题时,注意构造直角
三角形模型,结合方程进行求解.
