人教版高中物理选修3-4第十五章-相对论简介(共29张PPT)
文档属性
| 名称 | 人教版高中物理选修3-4第十五章-相对论简介(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-30 00:00:00 | ||
图片预览




文档简介
(共29张PPT)
相对论简介
相对论诞生的背景
在1900年英国皇家学会的新年庆祝会上,著名的物理学家,威廉·汤姆孙,回顾了物理学在过去几百年中的发展,充满自信地宣称:科学的大厦已经基本完成,未来的物理学家只要做一些修修补补的工作就可以了。
但同时他也承认“明朗的天空中还有两朵小小的、令人不安的乌云”
量子理论诞生
相对论诞生
与光速问题有关
与黑体辐射有关
正是这两朵小小的乌云,冲破了经典物理学的束缚,打消了当时绝大多数物理学家的盲目乐观情绪,为后来建立近代物理学的理论基础作出了贡献。
经典的相对性原理
1、惯性系:
牛顿运动定律成立的参考系
相对于一个惯性系做匀速直线运动的另一个参考系也是惯性系
2、伽利略相对性原理
力学规律在任何惯性系中都是相同的
还可表述为:在一个惯性参考系内进行的任何力学实验都不能判断这个惯性系是否相对于另一个惯性系做匀速直线运动;或者说,任何惯性系都是平权的。
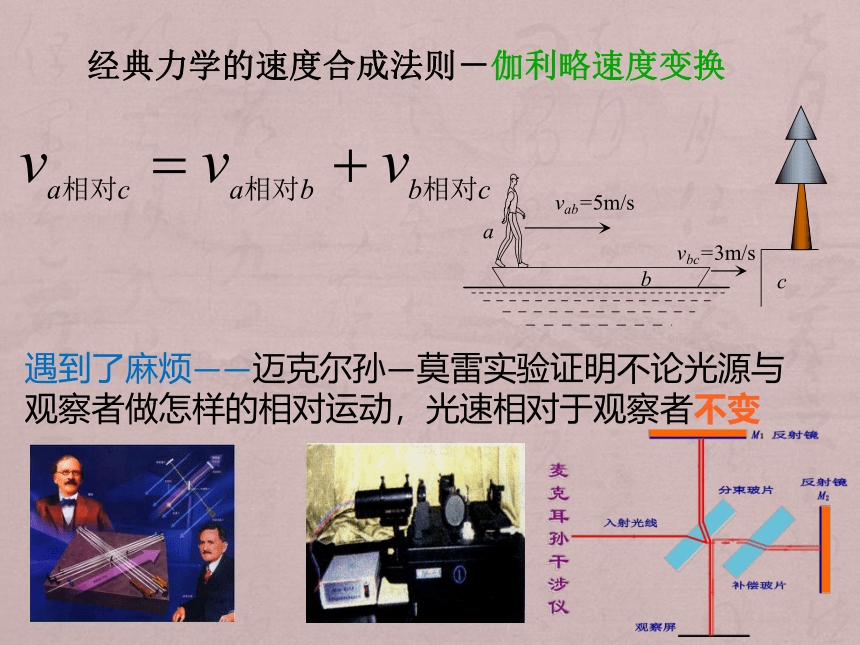
经典力学的速度合成法则-伽利略速度变换
遇到了麻烦——迈克尔孙—莫雷实验证明不论光源与观察者做怎样的相对运动,光速相对于观察者不变
a
b
c
vab=5m/s
vbc=3m/s
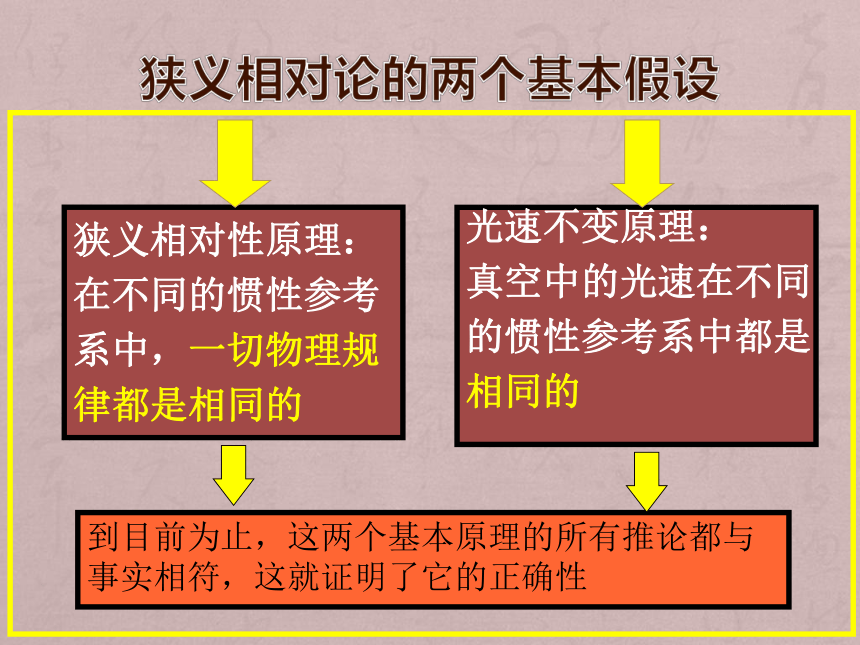
狭义相对论的两个基本假设
狭义相对性原理:
在不同的惯性参考
系中,一切物理规
律都是相同的
光速不变原理:
真空中的光速在不同
的惯性参考系中都是
相同的
到目前为止,这两个基本原理的所有推论都与事实相符,这就证明了它的正确性
狭义相对论推论——同时的相对性
思考一个问题:老师站在讲台前提问,坐在同一排上的一前一后的同学A 和同学B 举手了,老师说:“我看到两位同学同时举手了。”那么,按照你们现有的理论分析一下:两位同学的确是同时举手的吗?
对于“同时”的准确理解:两事件发生地离开观察者的距离相同,且观察者同时接收到两事件发出的光线。
日常生活中我们都相信“所见即所得”,对于眼睛看到的现象我们毫不犹豫的就认为是事物的本质,很少会深入思考,主要原因是低速的宏观世界里,光线传播的速度实在太快了,由于光线传播引起的时间差实在太微小了,但是精确的理论不能有丝毫误差,那么如此细微的差别也必须考虑在内。
狭义相对论推论——同时的相对性
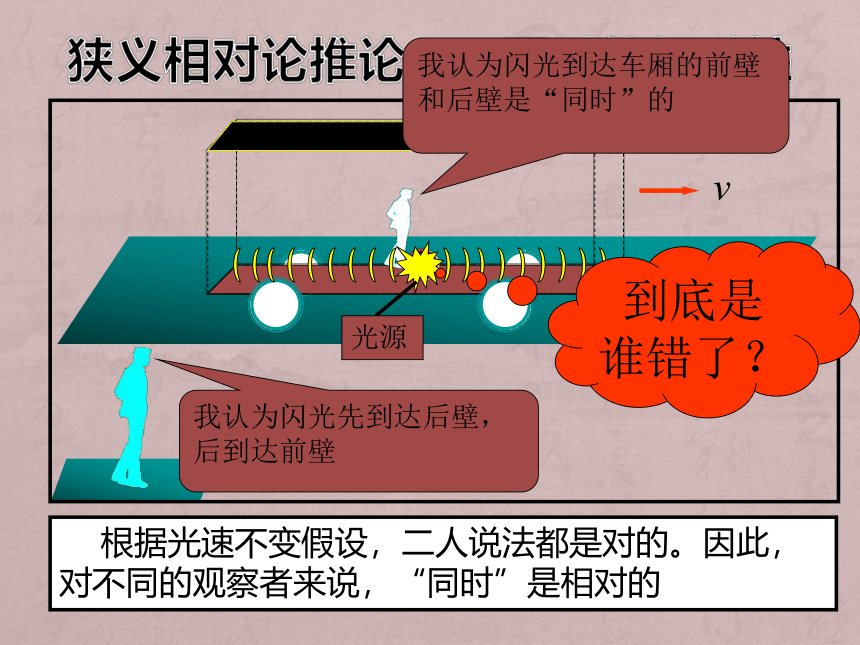
狭义相对论推论——同时的相对性
根据光速不变假设,二人说法都是对的。因此,对不同的观察者来说,“同时”是相对的
光源
我认为闪光到达车厢的前壁和后壁是“同时”的
我认为闪光先到达后壁,后到达前壁
到底是谁错了?
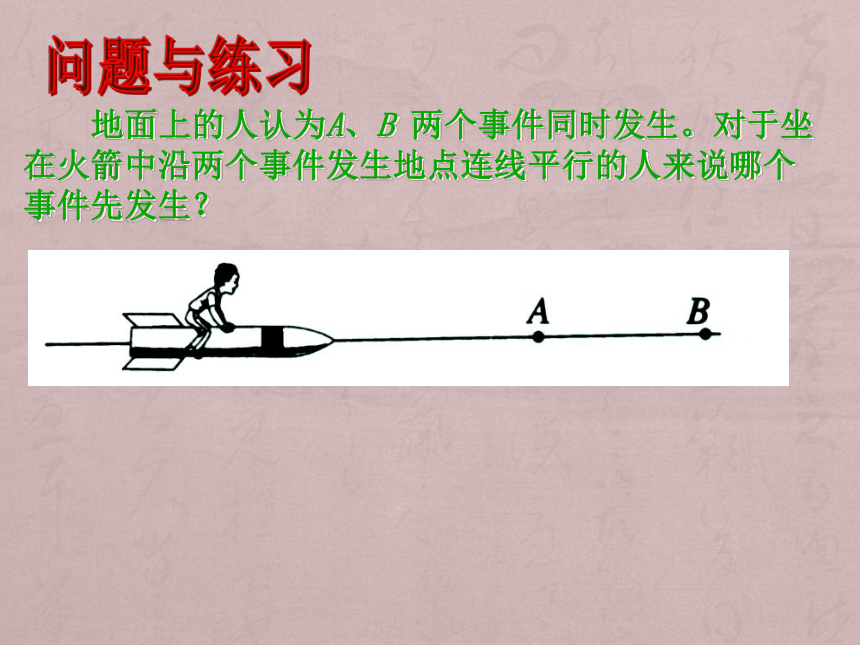
问题与练习
地面上的人认为A、B 两个事件同时发生。对于坐在火箭中沿两个事件发生地点连线平行的人来说哪个事件先发生?
狭义相对论推论——长度的相对性
v
※一火车以速度V 匀速行驶,地面有一人利用固定在地面上的尺子同时读出M、N两点的坐标,得出地面坐标系中杆的长度,对于车上的观察者会如何评论地面观察者的测量过程呢?试分析。
车上的观察者认为,地面参考系的人先读取N点的读数,而后才在M 点读数。
车上的人认为地面观察者把杆长测短了!
狭义相对论推论——时间的相对性
高速运行的列车上,由车厢底部发出的闪光,对于车上的人来说,闪光是在竖直方向反射的,而车厢外的人认为被接收的反射光是沿斜线传播的.
狭义相对论推论——时间的相对性
对于车厢内的人:
对于车厢外的人:
h
固有时间间隔(原时)
坐标时间间隔
动钟变慢
结论—时间膨胀或者动钟变慢效应:地面上看,运动的物体上的时间进程比地面上慢。
对于这个结论我们需要了解:
1、运动时钟变慢效应是时间本身的客观特征,即并非感觉
上变慢,而是真实的变慢。
2、这个时间进程包括物理、化学过程、生命过程,甚至人的动作、人的新陈代谢都变慢了。
3、这个效应是相对的,即运动的物体上的人认为一切都很
正常,而地面上的时间进程变慢了。
4、运动的速度越大,这个效应越明显。
时空相对性的实验验证
根据相对论,时间在运动中会进行的比较缓慢,也就是说,在空间中高速移动的时钟,比固定于地面上的时钟走得慢.
??1971年,科学家将铯原子钟放在喷气式飞机中作环球飞行,然后与地面的基准钟对照.实验结果与理论预言符合的很好.这是相对论的第一次宏观验证.
问题与练习
A、B、C是三个完全相同的时钟,A放在地面上,B、C分别放在两个火箭上,以速度vb和vc朝同一方向飞行,vb参考答案:由动钟变慢效应,速度越大,时间变慢效应越明显,所以在地面上的观察者来看,C 上的钟走得最慢,B 次之,A 上(地面上)的钟走得最快。
狭义相对论推论——长度的相对性
尺缩效应的简要推导:
S′
S
A
B
v
B
A
A
B
vΔt1
v
A
B
vΔt2
在火车参考系S′中观察者测得的长度为相对自己静止的长度l0,使用的时间为固有时间间隔Δt0,两者满足关系式:2l0=cΔt0
在地面参考系S中观察者测得的长度为相对自己运动时的长度l,使用的时间为坐标时间间隔Δt,在激光向右到达平面镜B的过程中满足: l+vΔt1=cΔt1;
向左回到A的过程中满足: l-vΔt2=cΔt2;
又:2l0=cΔt0
l+vΔt1=cΔt1;
l-vΔt2=cΔt2
两式相减:v(Δt1+Δt2)=c(Δt1-Δt2)
又:Δt1+Δt2=Δt
得: Δt1-Δt2=vΔt/c
两式相加:2l+v(Δt1-Δt2)=cΔt
2l+v2Δt/c=cΔt
解得:Δt=2lc/(c2-v2)
结论——长度收缩效应或尺缩效应:一条沿自身长度方向运动的杆,其长度总比静止时的长度小。
对于这个结论我们需要了解:
1、这个效应是真实存在的,并非幻觉。
2、仅在沿着运动方向上的长度会收缩,垂直于运动方向上的长度不会收缩。
3、这个效应是相对的,即高速运动的物体上的人也会看到地
面上的物体沿运动方向长度变短。
4、物体的运动速度越大收缩效应越明显。
有文献报道在高为1981m的山顶上测得563个?子进入大气层,在海平面测得408个。示意如图所示,已知 ?子下降速率0.995c,低速运动时的半衰期τ0为2.2?s,c表示真空中光速.试解释上述测得结果。
根据经典理论进行计算,过程如下:
与实际测到的结果相差很大。再用相对论的理论来解释一下,看看会有多大差距呢?
时空相对性的实验验证—— μ子验证尺缩钟慢效应
有文献报道在高为1981m的山顶上测得563个?子进入大气层,在海平面测得408个。示意如图所示,已知 ?子下降速率0.995c,低速运动时的半衰期τ0为2.2?s,c表示真空中光速.试解释上述测得结果。
时空相对性的实验验证—— μ子验证尺缩钟慢效应
按相对论理论计算
以地面为参考系,由于?子运行速度极快,所以其物理进
程变慢,?子的半衰期τ应该大于2.2?s,具体分析如下 :
可见用相对论理论解释与观测数据符合的较好。
若如果以?子为参考系,则山高1981米仅相当于 ,而其半衰期仍为2.2?s ,代入公式得到和上述一样的
表达式,结果还是456.9,说明此类问题用原有的经典理论已经无法解释,而相对论则可完美的进行解释。
时空相对性的实验验证—— μ子验证尺缩钟慢效应
狭义相对论的其他结论
经典力学的速度合成法则-伽利略速度变换
那么在高速运动的情况下,这样的速度合成公式还能用吗
?
【例题】(1)如果u′=0.6c,v=0.6c,它们的合速度会不会超过光速?(2)若u′=c,即在运动参考系中观察光的速度是c,求证: u=c,即在另一个参考系中光的速度也是c,而与v的大小无关;也就是光相对于任何一个参考系,速度均不变。
相对论速度变换公式:
相对论质量:
该式中m0为速度为零时的质量,称为静止质量,m为以速度v运动时的质量。
狭义相对论的其他结论
揭示了质量与能量之间存在一定的联系。质量和能量就是一个东西,是一个东西的两种表述。质量就是内敛的能量,能量就是外显的质量。
质能方程——改变世界的方程:E=mc2
狭义相对论的其他结论
静止能量E0=m0c2
相对论动能 Ek=mc2-m0c2
当v远小于c时:
相对论动量
当v远小于c时:p=m0v
相对论结论 经典力学
质量
m
时间
钟慢效应 t
长度 尺缩效应
速度
能量 E=mc2
动能 Ek=mc2-m0c2
动量
P=mv
当v ? c, ,意味着将一个静止质量不为零的粒子,使其速度达到光速,是不可能的。
【例题】有一粒子静止质量为m0,现以速度v=0.6c运动,它的质量________,动量__________,动能 ___________
当粒子速率为________时,其相对论动量等于非相对论动量的两倍
牛顿运动定律和光速不变
相对论质量
当 时
当 时
当 时
光子
当 时
动量与能量的关系
相对论结论 经典力学结论
对于光,E=pc
广义相对论和狭义相对论
狭义相对论
广义相对论
不同的惯性参考系中一切物理规律都是相同的
任何参考系(包括非惯性系)中物理规律都是相同的
真空中的光速在不同惯性参考系中都是相等的
一个均匀的引力场与一个做匀加速运动的参考系等价
更进一步
等效原理
光速恒定
爱因斯坦相对性原理
广义相对性原理
相对论简介
相对论诞生的背景
在1900年英国皇家学会的新年庆祝会上,著名的物理学家,威廉·汤姆孙,回顾了物理学在过去几百年中的发展,充满自信地宣称:科学的大厦已经基本完成,未来的物理学家只要做一些修修补补的工作就可以了。
但同时他也承认“明朗的天空中还有两朵小小的、令人不安的乌云”
量子理论诞生
相对论诞生
与光速问题有关
与黑体辐射有关
正是这两朵小小的乌云,冲破了经典物理学的束缚,打消了当时绝大多数物理学家的盲目乐观情绪,为后来建立近代物理学的理论基础作出了贡献。
经典的相对性原理
1、惯性系:
牛顿运动定律成立的参考系
相对于一个惯性系做匀速直线运动的另一个参考系也是惯性系
2、伽利略相对性原理
力学规律在任何惯性系中都是相同的
还可表述为:在一个惯性参考系内进行的任何力学实验都不能判断这个惯性系是否相对于另一个惯性系做匀速直线运动;或者说,任何惯性系都是平权的。
经典力学的速度合成法则-伽利略速度变换
遇到了麻烦——迈克尔孙—莫雷实验证明不论光源与观察者做怎样的相对运动,光速相对于观察者不变
a
b
c
vab=5m/s
vbc=3m/s
狭义相对论的两个基本假设
狭义相对性原理:
在不同的惯性参考
系中,一切物理规
律都是相同的
光速不变原理:
真空中的光速在不同
的惯性参考系中都是
相同的
到目前为止,这两个基本原理的所有推论都与事实相符,这就证明了它的正确性
狭义相对论推论——同时的相对性
思考一个问题:老师站在讲台前提问,坐在同一排上的一前一后的同学A 和同学B 举手了,老师说:“我看到两位同学同时举手了。”那么,按照你们现有的理论分析一下:两位同学的确是同时举手的吗?
对于“同时”的准确理解:两事件发生地离开观察者的距离相同,且观察者同时接收到两事件发出的光线。
日常生活中我们都相信“所见即所得”,对于眼睛看到的现象我们毫不犹豫的就认为是事物的本质,很少会深入思考,主要原因是低速的宏观世界里,光线传播的速度实在太快了,由于光线传播引起的时间差实在太微小了,但是精确的理论不能有丝毫误差,那么如此细微的差别也必须考虑在内。
狭义相对论推论——同时的相对性
狭义相对论推论——同时的相对性
根据光速不变假设,二人说法都是对的。因此,对不同的观察者来说,“同时”是相对的
光源
我认为闪光到达车厢的前壁和后壁是“同时”的
我认为闪光先到达后壁,后到达前壁
到底是谁错了?
问题与练习
地面上的人认为A、B 两个事件同时发生。对于坐在火箭中沿两个事件发生地点连线平行的人来说哪个事件先发生?
狭义相对论推论——长度的相对性
v
※一火车以速度V 匀速行驶,地面有一人利用固定在地面上的尺子同时读出M、N两点的坐标,得出地面坐标系中杆的长度,对于车上的观察者会如何评论地面观察者的测量过程呢?试分析。
车上的观察者认为,地面参考系的人先读取N点的读数,而后才在M 点读数。
车上的人认为地面观察者把杆长测短了!
狭义相对论推论——时间的相对性
高速运行的列车上,由车厢底部发出的闪光,对于车上的人来说,闪光是在竖直方向反射的,而车厢外的人认为被接收的反射光是沿斜线传播的.
狭义相对论推论——时间的相对性
对于车厢内的人:
对于车厢外的人:
h
固有时间间隔(原时)
坐标时间间隔
动钟变慢
结论—时间膨胀或者动钟变慢效应:地面上看,运动的物体上的时间进程比地面上慢。
对于这个结论我们需要了解:
1、运动时钟变慢效应是时间本身的客观特征,即并非感觉
上变慢,而是真实的变慢。
2、这个时间进程包括物理、化学过程、生命过程,甚至人的动作、人的新陈代谢都变慢了。
3、这个效应是相对的,即运动的物体上的人认为一切都很
正常,而地面上的时间进程变慢了。
4、运动的速度越大,这个效应越明显。
时空相对性的实验验证
根据相对论,时间在运动中会进行的比较缓慢,也就是说,在空间中高速移动的时钟,比固定于地面上的时钟走得慢.
??1971年,科学家将铯原子钟放在喷气式飞机中作环球飞行,然后与地面的基准钟对照.实验结果与理论预言符合的很好.这是相对论的第一次宏观验证.
问题与练习
A、B、C是三个完全相同的时钟,A放在地面上,B、C分别放在两个火箭上,以速度vb和vc朝同一方向飞行,vb
狭义相对论推论——长度的相对性
尺缩效应的简要推导:
S′
S
A
B
v
B
A
A
B
vΔt1
v
A
B
vΔt2
在火车参考系S′中观察者测得的长度为相对自己静止的长度l0,使用的时间为固有时间间隔Δt0,两者满足关系式:2l0=cΔt0
在地面参考系S中观察者测得的长度为相对自己运动时的长度l,使用的时间为坐标时间间隔Δt,在激光向右到达平面镜B的过程中满足: l+vΔt1=cΔt1;
向左回到A的过程中满足: l-vΔt2=cΔt2;
又:2l0=cΔt0
l+vΔt1=cΔt1;
l-vΔt2=cΔt2
两式相减:v(Δt1+Δt2)=c(Δt1-Δt2)
又:Δt1+Δt2=Δt
得: Δt1-Δt2=vΔt/c
两式相加:2l+v(Δt1-Δt2)=cΔt
2l+v2Δt/c=cΔt
解得:Δt=2lc/(c2-v2)
结论——长度收缩效应或尺缩效应:一条沿自身长度方向运动的杆,其长度总比静止时的长度小。
对于这个结论我们需要了解:
1、这个效应是真实存在的,并非幻觉。
2、仅在沿着运动方向上的长度会收缩,垂直于运动方向上的长度不会收缩。
3、这个效应是相对的,即高速运动的物体上的人也会看到地
面上的物体沿运动方向长度变短。
4、物体的运动速度越大收缩效应越明显。
有文献报道在高为1981m的山顶上测得563个?子进入大气层,在海平面测得408个。示意如图所示,已知 ?子下降速率0.995c,低速运动时的半衰期τ0为2.2?s,c表示真空中光速.试解释上述测得结果。
根据经典理论进行计算,过程如下:
与实际测到的结果相差很大。再用相对论的理论来解释一下,看看会有多大差距呢?
时空相对性的实验验证—— μ子验证尺缩钟慢效应
有文献报道在高为1981m的山顶上测得563个?子进入大气层,在海平面测得408个。示意如图所示,已知 ?子下降速率0.995c,低速运动时的半衰期τ0为2.2?s,c表示真空中光速.试解释上述测得结果。
时空相对性的实验验证—— μ子验证尺缩钟慢效应
按相对论理论计算
以地面为参考系,由于?子运行速度极快,所以其物理进
程变慢,?子的半衰期τ应该大于2.2?s,具体分析如下 :
可见用相对论理论解释与观测数据符合的较好。
若如果以?子为参考系,则山高1981米仅相当于 ,而其半衰期仍为2.2?s ,代入公式得到和上述一样的
表达式,结果还是456.9,说明此类问题用原有的经典理论已经无法解释,而相对论则可完美的进行解释。
时空相对性的实验验证—— μ子验证尺缩钟慢效应
狭义相对论的其他结论
经典力学的速度合成法则-伽利略速度变换
那么在高速运动的情况下,这样的速度合成公式还能用吗
?
【例题】(1)如果u′=0.6c,v=0.6c,它们的合速度会不会超过光速?(2)若u′=c,即在运动参考系中观察光的速度是c,求证: u=c,即在另一个参考系中光的速度也是c,而与v的大小无关;也就是光相对于任何一个参考系,速度均不变。
相对论速度变换公式:
相对论质量:
该式中m0为速度为零时的质量,称为静止质量,m为以速度v运动时的质量。
狭义相对论的其他结论
揭示了质量与能量之间存在一定的联系。质量和能量就是一个东西,是一个东西的两种表述。质量就是内敛的能量,能量就是外显的质量。
质能方程——改变世界的方程:E=mc2
狭义相对论的其他结论
静止能量E0=m0c2
相对论动能 Ek=mc2-m0c2
当v远小于c时:
相对论动量
当v远小于c时:p=m0v
相对论结论 经典力学
质量
m
时间
钟慢效应 t
长度 尺缩效应
速度
能量 E=mc2
动能 Ek=mc2-m0c2
动量
P=mv
当v ? c, ,意味着将一个静止质量不为零的粒子,使其速度达到光速,是不可能的。
【例题】有一粒子静止质量为m0,现以速度v=0.6c运动,它的质量________,动量__________,动能 ___________
当粒子速率为________时,其相对论动量等于非相对论动量的两倍
牛顿运动定律和光速不变
相对论质量
当 时
当 时
当 时
光子
当 时
动量与能量的关系
相对论结论 经典力学结论
对于光,E=pc
广义相对论和狭义相对论
狭义相对论
广义相对论
不同的惯性参考系中一切物理规律都是相同的
任何参考系(包括非惯性系)中物理规律都是相同的
真空中的光速在不同惯性参考系中都是相等的
一个均匀的引力场与一个做匀加速运动的参考系等价
更进一步
等效原理
光速恒定
爱因斯坦相对性原理
广义相对性原理
