3.2 系统的分析
图片预览





文档简介
(共12张PPT)
3.2 系统的分析
学习目标:
1.初步掌握系统分析的基本方法。
2.理解系统优化的意义,能结合实例分析影响系统优化的因素。
东莞市光明中学 黄利辉
一、系统分析及其一般步骤
1、什么是系统分析
为了发挥系统的功能,实现系统的目标,运用科学的方法对系统加以周详的考察、分析、比较、试验,并在此基础上拟订一套有效的处理步骤和程序,或对原有的系统提出改正方案的过程。
特点:
完整地而不是零星地处理问题,考虑各种主要变化因素及其相互的影响,全面地思考和解决问题。
作用:
可以正确地提出整体目标,恰当地选择方案,科学地确定行动的方略。
案例分析:汉字激光照排系统
思考:
在汉字照排方案的决策中,系统的整体目标是什么?你认为王选进行决策的依据主要有哪些?
如何解决汉字的存储和输出:一是汉字字形信息量大,要解决字型信息量压缩问题;二是汉字字形信息压缩后存入计算机,需要将其快速还原和输出.
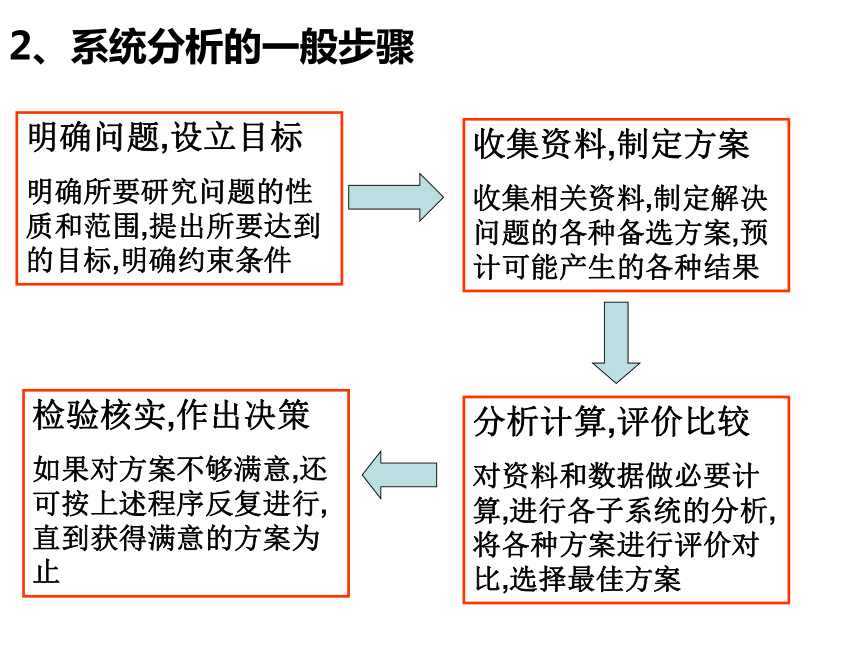
2、系统分析的一般步骤
明确问题,设立目标
明确所要研究问题的性质和范围,提出所要达到的目标,明确约束条件
收集资料,制定方案
收集相关资料,制定解决问题的各种备选方案,预计可能产生的各种结果
分析计算,评价比较
对资料和数据做必要计算,进行各子系统的分析,将各种方案进行评价对比,选择最佳方案
检验核实,作出决策
如果对方案不够满意,还可按上述程序反复进行,直到获得满意的方案为止
案例分析:田忌赛马
思考:
1、田忌与齐王的三局赛马可以有哪几种方案?
2、孙膑所出的主意,为什么能使田忌赢得胜利?
田忌—齐王 田忌—齐王
方案一 上马—上马 中马—中马 下马—下马
方案二 上马—上马 下马—中马 中马—下马
方案三 中马—上马 上马—中马 下马—下马
方案四 中马—上马 下马—中马 上马—下马
方案五 下马—上马 上马—中马 中马—下马
方案六 下马—上马 中马—中马 上马—下马
0:3
1:2
1:2
1:2
2:1
1:2
2:1
3、系统分析的主要原则
(1)整体性原则——系统分析首先要着眼于系统整体,要先分析整体,再分析部分;先看全局,后看局部;先看全过程,再看某一阶段;要考虑长远,不能只顾眼前。
阅读案例:《丁谓修皇宫》
(2)科学性原则
——系统分析要尽可能运用科学方法和数学工具进行定量分析,使决策的过程和结果更具有说服力。
阅读:优选法
(3)综合性原则
——系统分析总是为实现系统目标服务的。当系统存在若干个目标时,应将目标排出优先次序,首先选取最优的目标,然后尽可能在不损害第一个目标的前提下完成下一个目标。
注重研究系统各部分之间的相互联系和相互作用,既注重研究各部分间的横向联系,也注重研究各部分之间的纵向联系,既考虑当前,也要考虑长远。分析的基本思路是“综合——部分——综合”
即:要综合分析,统筹兼顾,不可顾此失彼,因小失大。
二、系统的优化
系统的优化是指在给定的条件下,根据系统的优化目标,采取一定的手段和方法,使系统的目标值达到最大化(或最小化)。
或者说:从多种可行方案或技术手段中得出最优的目标。
阅读案例: 农作物种植系统的优化——农业间作套种
案例: 利润问题
某家具厂要安排一周的生产计划,产品是桌子和椅子。制作一张桌子需4m2木板及时性20小时的工时,制作一只椅子需6m2木板及18小时的工时,每周能拥有的木板是600m2,可利用的工时是400小时;每张桌子的利润是50元,每只椅子的利润是60元。按合同每周至少要交付8张桌子和5只椅子,并假定所有的产品都能够销售出去。
问:该厂每周生产桌子和椅子的数量分别是多少时,能获得最大利润?
Smax=50x+60y
4x+6y≤600
20x+18y≤400
x≥8, y≥5
设每周生产桌子X张,生产椅子Y张,则有:
阅读:数学模型
用数学公式、图表等描述客观事物的特征模型,称为数学模型。
现实世界的事物与数学模型的关系可表示为:
抽象
现实世界的原型
对原型的分析
数学结论
数学模型
分析
解释
分析
案例:装修施工的组织优化
装修进度(周)
3 6 9 12
A 水电 K
木工 K
油漆 K
B 水电 K
木工 K
油漆 K
C 水电 K
木工 K
油漆 K
流水施工
优点:
(1)工期____
(2)需要水电、木工和油漆各____个装修队同时工作。
(3)相对于平行施工的方式,这种方式在施工时间内投入的人力、施工设备、材料____。
阅读: 系统工程
系统工程是指在系统思想的指导下,综合应用自然科学和社会科学中有关的先进思想、理论、方法和工具,对系统的结构、功能、要素、信息和反馈等进行分析、处理,解决实际问题,以达到最优规划、最优设计、最优管理和最优控制的目的。
3.2 系统的分析
学习目标:
1.初步掌握系统分析的基本方法。
2.理解系统优化的意义,能结合实例分析影响系统优化的因素。
东莞市光明中学 黄利辉
一、系统分析及其一般步骤
1、什么是系统分析
为了发挥系统的功能,实现系统的目标,运用科学的方法对系统加以周详的考察、分析、比较、试验,并在此基础上拟订一套有效的处理步骤和程序,或对原有的系统提出改正方案的过程。
特点:
完整地而不是零星地处理问题,考虑各种主要变化因素及其相互的影响,全面地思考和解决问题。
作用:
可以正确地提出整体目标,恰当地选择方案,科学地确定行动的方略。
案例分析:汉字激光照排系统
思考:
在汉字照排方案的决策中,系统的整体目标是什么?你认为王选进行决策的依据主要有哪些?
如何解决汉字的存储和输出:一是汉字字形信息量大,要解决字型信息量压缩问题;二是汉字字形信息压缩后存入计算机,需要将其快速还原和输出.
2、系统分析的一般步骤
明确问题,设立目标
明确所要研究问题的性质和范围,提出所要达到的目标,明确约束条件
收集资料,制定方案
收集相关资料,制定解决问题的各种备选方案,预计可能产生的各种结果
分析计算,评价比较
对资料和数据做必要计算,进行各子系统的分析,将各种方案进行评价对比,选择最佳方案
检验核实,作出决策
如果对方案不够满意,还可按上述程序反复进行,直到获得满意的方案为止
案例分析:田忌赛马
思考:
1、田忌与齐王的三局赛马可以有哪几种方案?
2、孙膑所出的主意,为什么能使田忌赢得胜利?
田忌—齐王 田忌—齐王
方案一 上马—上马 中马—中马 下马—下马
方案二 上马—上马 下马—中马 中马—下马
方案三 中马—上马 上马—中马 下马—下马
方案四 中马—上马 下马—中马 上马—下马
方案五 下马—上马 上马—中马 中马—下马
方案六 下马—上马 中马—中马 上马—下马
0:3
1:2
1:2
1:2
2:1
1:2
2:1
3、系统分析的主要原则
(1)整体性原则——系统分析首先要着眼于系统整体,要先分析整体,再分析部分;先看全局,后看局部;先看全过程,再看某一阶段;要考虑长远,不能只顾眼前。
阅读案例:《丁谓修皇宫》
(2)科学性原则
——系统分析要尽可能运用科学方法和数学工具进行定量分析,使决策的过程和结果更具有说服力。
阅读:优选法
(3)综合性原则
——系统分析总是为实现系统目标服务的。当系统存在若干个目标时,应将目标排出优先次序,首先选取最优的目标,然后尽可能在不损害第一个目标的前提下完成下一个目标。
注重研究系统各部分之间的相互联系和相互作用,既注重研究各部分间的横向联系,也注重研究各部分之间的纵向联系,既考虑当前,也要考虑长远。分析的基本思路是“综合——部分——综合”
即:要综合分析,统筹兼顾,不可顾此失彼,因小失大。
二、系统的优化
系统的优化是指在给定的条件下,根据系统的优化目标,采取一定的手段和方法,使系统的目标值达到最大化(或最小化)。
或者说:从多种可行方案或技术手段中得出最优的目标。
阅读案例: 农作物种植系统的优化——农业间作套种
案例: 利润问题
某家具厂要安排一周的生产计划,产品是桌子和椅子。制作一张桌子需4m2木板及时性20小时的工时,制作一只椅子需6m2木板及18小时的工时,每周能拥有的木板是600m2,可利用的工时是400小时;每张桌子的利润是50元,每只椅子的利润是60元。按合同每周至少要交付8张桌子和5只椅子,并假定所有的产品都能够销售出去。
问:该厂每周生产桌子和椅子的数量分别是多少时,能获得最大利润?
Smax=50x+60y
4x+6y≤600
20x+18y≤400
x≥8, y≥5
设每周生产桌子X张,生产椅子Y张,则有:
阅读:数学模型
用数学公式、图表等描述客观事物的特征模型,称为数学模型。
现实世界的事物与数学模型的关系可表示为:
抽象
现实世界的原型
对原型的分析
数学结论
数学模型
分析
解释
分析
案例:装修施工的组织优化
装修进度(周)
3 6 9 12
A 水电 K
木工 K
油漆 K
B 水电 K
木工 K
油漆 K
C 水电 K
木工 K
油漆 K
流水施工
优点:
(1)工期____
(2)需要水电、木工和油漆各____个装修队同时工作。
(3)相对于平行施工的方式,这种方式在施工时间内投入的人力、施工设备、材料____。
阅读: 系统工程
系统工程是指在系统思想的指导下,综合应用自然科学和社会科学中有关的先进思想、理论、方法和工具,对系统的结构、功能、要素、信息和反馈等进行分析、处理,解决实际问题,以达到最优规划、最优设计、最优管理和最优控制的目的。
