人教版数学七年级下册课件:7.2.2 用坐标表示平移(共22张PPT)
文档属性
| 名称 | 人教版数学七年级下册课件:7.2.2 用坐标表示平移(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
-
7.2.2
用坐标表示平移
平面直角坐标系
第七章
三维目标?
1、知识与技能:?掌握点的平移规律,图形平移与坐标变化的关系,能利用点的平移规律将平面图形进行平移.
2、过程与方法: 经历点的坐标变化与图形变化之间关系的探索过程,感受并了解图形的平移变化与点的坐标变化之间的关系
3、情感态度价值观:学会主动寻求解决问题的途径,从成功中体会研究数学问题的乐趣,从而增强学习数学的兴趣,树立学好数学的信心。
重点:理解坐标与平移变换之间的关系,会用坐标表示平移。难点:探究坐标与平移变换之间的关系。
ABOUT US
复习回顾
1.什么叫做平移?
2.平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
平移后图形的位置改变,形状、大小不变。
ABOUT US
复习回顾
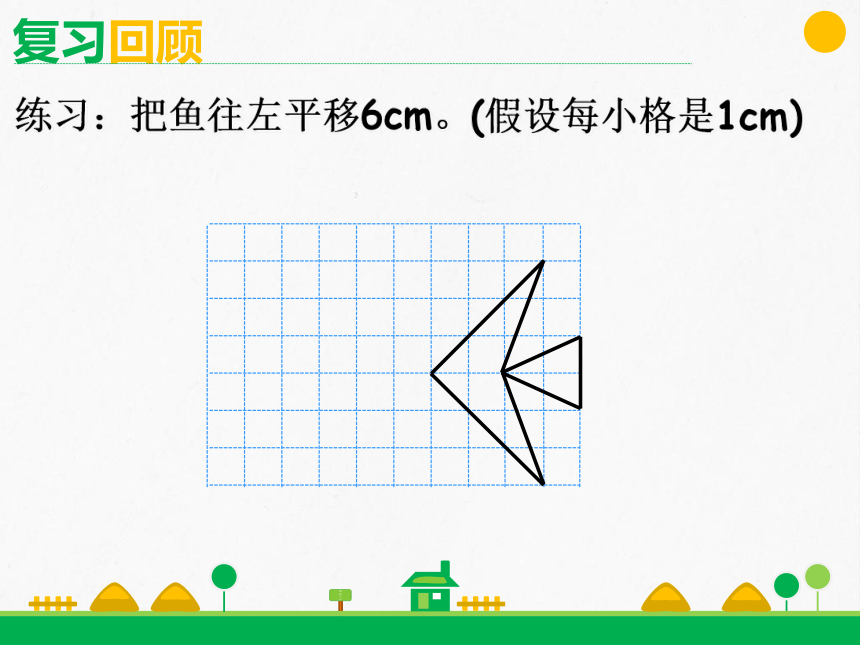
练习:把鱼往左平移6cm。(假设每小格是1cm)
ABOUT US
复习回顾
练习:把鱼往左平移6cm。(假设每小格是1cm)
ABOUT US
复习回顾
练习:把鱼往左平移6cm。(假设每小格是1cm)
思考探究
?
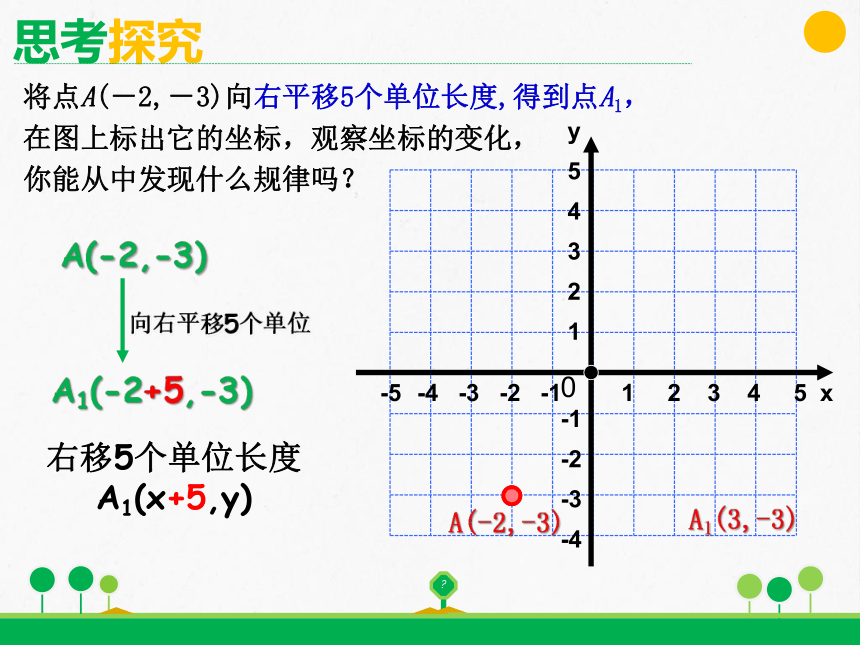
将点A(-2,-3)向右平移5个单位长度,得到点A1,
在图上标出它的坐标,观察坐标的变化,
你能从中发现什么规律吗?
0
-1
-2
-3
-4
-5 -4 -3 -2 -1 1 2 3 4 5 x
y
5
4
3
2
1
A(-2,-3)
A1(3,-3)
向右平移5个单位
A(-2,-3)
A1(-2+5,-3)
右移5个单位长度
A1(x+5,y)
思考探究
?
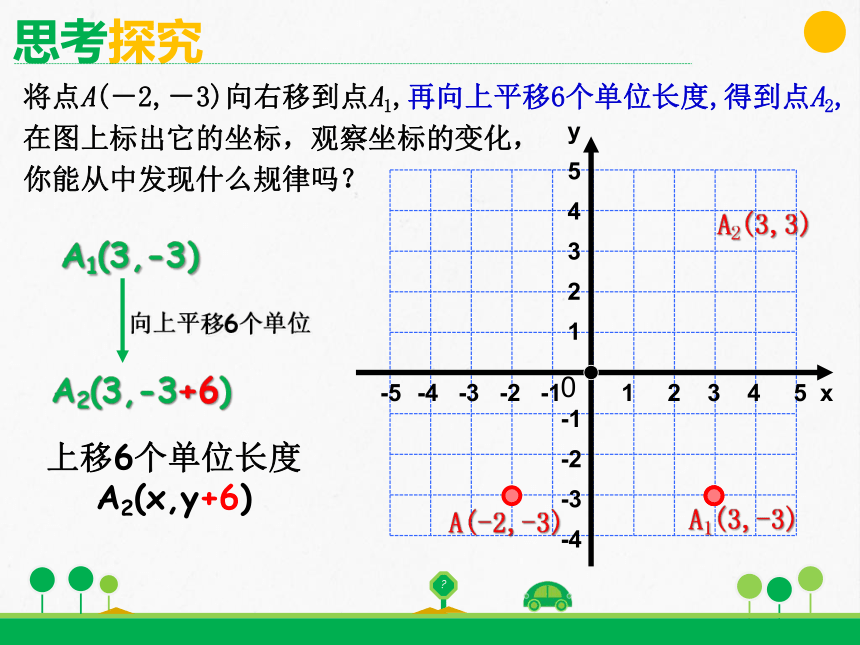
将点A(-2,-3)向右移到点A1,再向上平移6个单位长度,得到点A2,
在图上标出它的坐标,观察坐标的变化,
你能从中发现什么规律吗?
0
-1
-2
-3
-4
-5 -4 -3 -2 -1 1 2 3 4 5 x
y
5
4
3
2
1
A(-2,-3)
A1(3,-3)
向上平移6个单位
A1(3,-3)
A2(3,-3+6)
上移6个单位长度
A2(x,y+6)
A2(3,3)
思考探究
?
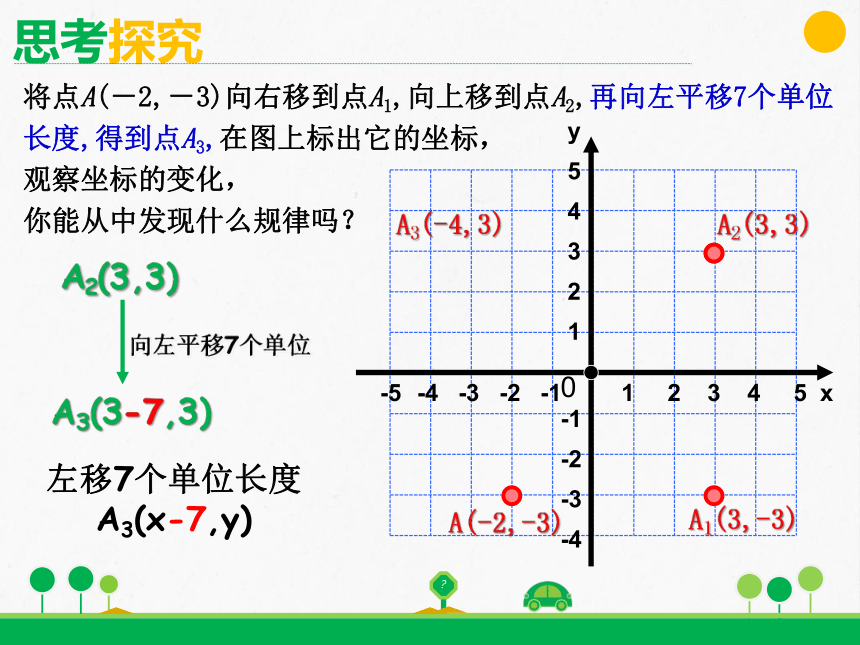
将点A(-2,-3)向右移到点A1,向上移到点A2,再向左平移7个单位长度,得到点A3,在图上标出它的坐标,
观察坐标的变化,
你能从中发现什么规律吗?
0
-1
-2
-3
-4
-5 -4 -3 -2 -1 1 2 3 4 5 x
y
5
4
3
2
1
A(-2,-3)
A1(3,-3)
向左平移7个单位
A2(3,3)
A3(3-7,3)
左移7个单位长度
A3(x-7,y)
A2(3,3)
A3(-4,3)
思考探究
?
将点A(-2,-3)向右移到点A1,向上移到点A2,向左移到点A3,
再向下平移2个单位长度,得到点A4,
在图上标出它的坐标,观察坐标的变化,
你能从中发现什么规律吗?
0
-1
-2
-3
-4
-5 -4 -3 -2 -1 1 2 3 4 5 x
y
5
4
3
2
1
A(-2,-3)
A1(3,-3)
向下平移2个单位
A3(-4,3)
A4(-4,3-2)
下移2个单位长度
A4(x,y-2)
A2(3,3)
A3(-4,3)
A4(-4,1)
思考探究
?
右移5个单位长度,A1(x+5,y)
上移6个单位长度,A2(x,y+6)
下移2个单位长度,A4(x,y-2)
左移7个单位长度,A3(x-7,y)
与横坐标x有关
右加左减
与纵坐标y有关
上加下减
简记:右加左减,
上加下减
知识讲解:点平移与坐标变化
A(x,y)
左移a个
单位长度
A2(x-a,y)
右移a个
单位长度
A1(x+a,y)
上移a个
单位长度
A3(x,y+a)
下移a个
单位长度
A4(x,y-a)
巩固练习:
【例1】将点(1,-2)向右平移3个单位得到新点的坐标为( )
A.(1,-5) B.(4,-2) C.(1,1) D.(-2,2)
B
1.在平面直角坐标系中,将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点A',则点A'的坐标是( )
A.(-1,1) B.(-1,-2) C.(-1,2) D.(1,2)
A
巩固练习:
【例2】平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2) C.(-6,-1) D.(0,-1)
C
2.在平面直角坐标系中,将点P(-2,1)向右平移3个单位长度,再向下平移4个单位长度得到点P′的坐标是( )
A.(2,4) B.(1,-3) C.(1,5) D.(-5,5)
B
正方形ABCD四个顶点分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD平移后四个顶点相应变为点E,F,G,H.
点E,F,G,H坐标分别是什么?
思考探究
?
0
-1
-2
-3
-4
-2 -1 1 2 3 4 5 6 7 x
y
4
3
2
1
A
B
C
D
E
F
G
H
8个单位长度
7个单位长度
A(-2,4)
B(-2,3)
C(-1,3)
D(-1,4)
-7
+8
E(6,-3)
F(6,-4)
G(7,-4)
H(7,-3)
图形的斜向平移,
可通过图形的水平平移和垂直平移来完成
例题讲解:平面直角坐标
如图,△ABC三个顶点的坐标 A(4,3),B(3,1),C(1,2)
(1)将三角形ABC三个顶点的
横坐标都减去6,纵坐标不变
则有A1 ,
B1 , C1 。
(-2,3)
(-3,1)
(-5,2)
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
△A1B1C1是△ABC向左平移6个单位长度得到的
猜想:
△A1B1C1与△ABC的大小、形状和位置上有什么关系,为什么?
则有A2 ,
B2 , C2 。
例题讲解:平面直角坐标
(4,-2)
(3,-4)
(1,-3)
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
△A2B2C2是△ABC向下平移5个单位长度得到的
A2
B2
C2
(4,-2)
(3,-4)
(1,-3)
如图,△ABC三个顶点的坐标 A(4,3),B(3,1),C(1,2)
(2)将三角形ABC三个顶点的
纵坐标都减去5,横坐标不变
猜想:
△A2B2C2与△ABC的大小、形状和位置上有什么关系,为什么?
巩固练习:
【例3】如图所示,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
A
A. 先向左平移5个单位,
再向下平移2个单位
B. 先向右平移5个单位,
再向下平移2个单位
C. 先向左平移5个单位,
再向上平移2个单位
D. 先向右平移5个单位,
再向上平移2个单位
巩固练习:
3.在6×6方格中,将图①中的图形N平移后位置如图②所示,则图形N的平移方法中,正确的是( )
A.向下移动1格 B.向上移动1格
C.向上移动2格 D.向下移动2格
D
巩固练习:
【例4】如图,在平面直角坐标系中,A(-3,2),B(-1,0),C(-1,3),将△ABC向右平移4个单位,再向下平移3个单位,得到△A1B1C1,点A,B,C的对应点分别A1,B1,C1,则点A1的坐标为( )
A.(3,-3) B.(1,-1)
C.(3,0) D.(2,-1)
B
A(1,-1)
巩固练习:
4.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-2,3),
B(-3,1),C(-1,2),若将△ABC平移后,点A的对应点A1的坐标为(1,2),则点C的对应点C1的坐标为( )
A.(-1,5) B.(2,2)
C.(3,1) D.(2,1)
D
A1(1,2)
课堂小结
简记:右加左减,
上加下减
点平移与坐标变化
A(x,y)
左移a个
单位长度
A2(x-a,y)
右移a个
单位长度
A1(x+a,y)
上移a个
单位长度
A3(x,y+a)
下移a个
单位长度
A4(x,y-a)
-
7.2.2
用坐标表示平移
平面直角坐标系
第七章
三维目标?
1、知识与技能:?掌握点的平移规律,图形平移与坐标变化的关系,能利用点的平移规律将平面图形进行平移.
2、过程与方法: 经历点的坐标变化与图形变化之间关系的探索过程,感受并了解图形的平移变化与点的坐标变化之间的关系
3、情感态度价值观:学会主动寻求解决问题的途径,从成功中体会研究数学问题的乐趣,从而增强学习数学的兴趣,树立学好数学的信心。
重点:理解坐标与平移变换之间的关系,会用坐标表示平移。难点:探究坐标与平移变换之间的关系。
ABOUT US
复习回顾
1.什么叫做平移?
2.平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
平移后图形的位置改变,形状、大小不变。
ABOUT US
复习回顾
练习:把鱼往左平移6cm。(假设每小格是1cm)
ABOUT US
复习回顾
练习:把鱼往左平移6cm。(假设每小格是1cm)
ABOUT US
复习回顾
练习:把鱼往左平移6cm。(假设每小格是1cm)
思考探究
?
将点A(-2,-3)向右平移5个单位长度,得到点A1,
在图上标出它的坐标,观察坐标的变化,
你能从中发现什么规律吗?
0
-1
-2
-3
-4
-5 -4 -3 -2 -1 1 2 3 4 5 x
y
5
4
3
2
1
A(-2,-3)
A1(3,-3)
向右平移5个单位
A(-2,-3)
A1(-2+5,-3)
右移5个单位长度
A1(x+5,y)
思考探究
?
将点A(-2,-3)向右移到点A1,再向上平移6个单位长度,得到点A2,
在图上标出它的坐标,观察坐标的变化,
你能从中发现什么规律吗?
0
-1
-2
-3
-4
-5 -4 -3 -2 -1 1 2 3 4 5 x
y
5
4
3
2
1
A(-2,-3)
A1(3,-3)
向上平移6个单位
A1(3,-3)
A2(3,-3+6)
上移6个单位长度
A2(x,y+6)
A2(3,3)
思考探究
?
将点A(-2,-3)向右移到点A1,向上移到点A2,再向左平移7个单位长度,得到点A3,在图上标出它的坐标,
观察坐标的变化,
你能从中发现什么规律吗?
0
-1
-2
-3
-4
-5 -4 -3 -2 -1 1 2 3 4 5 x
y
5
4
3
2
1
A(-2,-3)
A1(3,-3)
向左平移7个单位
A2(3,3)
A3(3-7,3)
左移7个单位长度
A3(x-7,y)
A2(3,3)
A3(-4,3)
思考探究
?
将点A(-2,-3)向右移到点A1,向上移到点A2,向左移到点A3,
再向下平移2个单位长度,得到点A4,
在图上标出它的坐标,观察坐标的变化,
你能从中发现什么规律吗?
0
-1
-2
-3
-4
-5 -4 -3 -2 -1 1 2 3 4 5 x
y
5
4
3
2
1
A(-2,-3)
A1(3,-3)
向下平移2个单位
A3(-4,3)
A4(-4,3-2)
下移2个单位长度
A4(x,y-2)
A2(3,3)
A3(-4,3)
A4(-4,1)
思考探究
?
右移5个单位长度,A1(x+5,y)
上移6个单位长度,A2(x,y+6)
下移2个单位长度,A4(x,y-2)
左移7个单位长度,A3(x-7,y)
与横坐标x有关
右加左减
与纵坐标y有关
上加下减
简记:右加左减,
上加下减
知识讲解:点平移与坐标变化
A(x,y)
左移a个
单位长度
A2(x-a,y)
右移a个
单位长度
A1(x+a,y)
上移a个
单位长度
A3(x,y+a)
下移a个
单位长度
A4(x,y-a)
巩固练习:
【例1】将点(1,-2)向右平移3个单位得到新点的坐标为( )
A.(1,-5) B.(4,-2) C.(1,1) D.(-2,2)
B
1.在平面直角坐标系中,将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点A',则点A'的坐标是( )
A.(-1,1) B.(-1,-2) C.(-1,2) D.(1,2)
A
巩固练习:
【例2】平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2) C.(-6,-1) D.(0,-1)
C
2.在平面直角坐标系中,将点P(-2,1)向右平移3个单位长度,再向下平移4个单位长度得到点P′的坐标是( )
A.(2,4) B.(1,-3) C.(1,5) D.(-5,5)
B
正方形ABCD四个顶点分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD平移后四个顶点相应变为点E,F,G,H.
点E,F,G,H坐标分别是什么?
思考探究
?
0
-1
-2
-3
-4
-2 -1 1 2 3 4 5 6 7 x
y
4
3
2
1
A
B
C
D
E
F
G
H
8个单位长度
7个单位长度
A(-2,4)
B(-2,3)
C(-1,3)
D(-1,4)
-7
+8
E(6,-3)
F(6,-4)
G(7,-4)
H(7,-3)
图形的斜向平移,
可通过图形的水平平移和垂直平移来完成
例题讲解:平面直角坐标
如图,△ABC三个顶点的坐标 A(4,3),B(3,1),C(1,2)
(1)将三角形ABC三个顶点的
横坐标都减去6,纵坐标不变
则有A1 ,
B1 , C1 。
(-2,3)
(-3,1)
(-5,2)
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
△A1B1C1是△ABC向左平移6个单位长度得到的
猜想:
△A1B1C1与△ABC的大小、形状和位置上有什么关系,为什么?
则有A2 ,
B2 , C2 。
例题讲解:平面直角坐标
(4,-2)
(3,-4)
(1,-3)
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
△A2B2C2是△ABC向下平移5个单位长度得到的
A2
B2
C2
(4,-2)
(3,-4)
(1,-3)
如图,△ABC三个顶点的坐标 A(4,3),B(3,1),C(1,2)
(2)将三角形ABC三个顶点的
纵坐标都减去5,横坐标不变
猜想:
△A2B2C2与△ABC的大小、形状和位置上有什么关系,为什么?
巩固练习:
【例3】如图所示,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
A
A. 先向左平移5个单位,
再向下平移2个单位
B. 先向右平移5个单位,
再向下平移2个单位
C. 先向左平移5个单位,
再向上平移2个单位
D. 先向右平移5个单位,
再向上平移2个单位
巩固练习:
3.在6×6方格中,将图①中的图形N平移后位置如图②所示,则图形N的平移方法中,正确的是( )
A.向下移动1格 B.向上移动1格
C.向上移动2格 D.向下移动2格
D
巩固练习:
【例4】如图,在平面直角坐标系中,A(-3,2),B(-1,0),C(-1,3),将△ABC向右平移4个单位,再向下平移3个单位,得到△A1B1C1,点A,B,C的对应点分别A1,B1,C1,则点A1的坐标为( )
A.(3,-3) B.(1,-1)
C.(3,0) D.(2,-1)
B
A(1,-1)
巩固练习:
4.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-2,3),
B(-3,1),C(-1,2),若将△ABC平移后,点A的对应点A1的坐标为(1,2),则点C的对应点C1的坐标为( )
A.(-1,5) B.(2,2)
C.(3,1) D.(2,1)
D
A1(1,2)
课堂小结
简记:右加左减,
上加下减
点平移与坐标变化
A(x,y)
左移a个
单位长度
A2(x-a,y)
右移a个
单位长度
A1(x+a,y)
上移a个
单位长度
A3(x,y+a)
下移a个
单位长度
A4(x,y-a)
