华师大版数学八年级下册17.3.3一次函数的性质课件(19张PPT)
文档属性
| 名称 | 华师大版数学八年级下册17.3.3一次函数的性质课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 634.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 09:49:55 | ||
图片预览






文档简介
课件19张PPT。3.一次函数的性质1.一次函数性质的理解和应用.(重点)
2.一次函数性质的灵活应用.(难点)一、探究:一次函数的性质
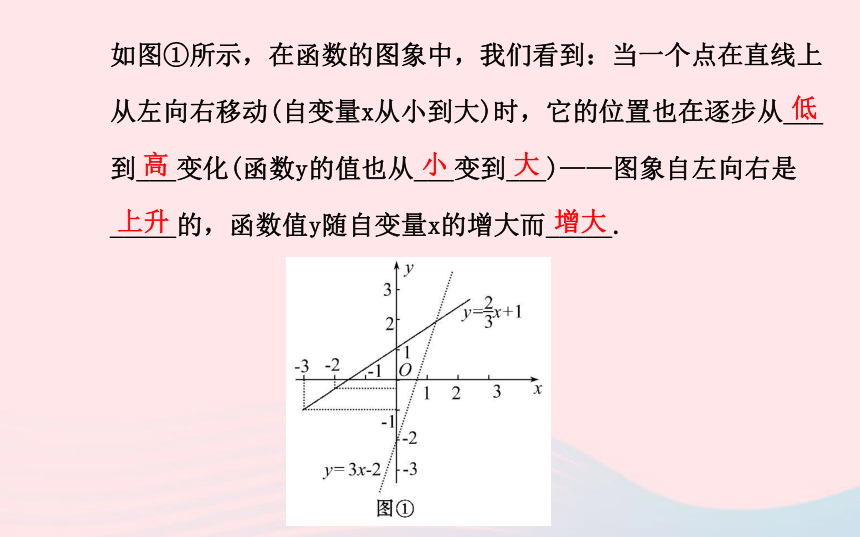
观察函数y=3x-2,y= +1,y=-x+2,y= -1的图象.如图①所示,在函数的图象中,我们看到:当一个点在直线上
从左向右移动(自变量x从小到大)时,它的位置也在逐步从___
到___变化(函数y的值也从___变到___)——图象自左向右是
_____的,函数值y随自变量x的增大而_____.低小大上升增大高在图②中我们看到:当一个点在直线上从左向右移动(自变量x
从小到大)时,它的位置在逐步从___到___变化(函数y的值从
___变到___)——图象自左向右是_____的,函数值y随自变量x
的增大而_____.高低大小下降减小【总结】一次函数y=kx+b(k≠0)的性质:
(1)当k>0时,y随x的增大而_____,这时函数图象从左到右
_____.
(2)当k<0时,y随x的增大而_____,这时函数图象从左到右
_____.增大上升减小下降二、结合图象理解一次函数y=kx+b(k,b为常数,k≠0)的性质一、二、三一、三、四一、二、四二、三、四增大增大减小减小 (打“√”或“×”)
(1)对一次函数y=kx+b(k≠0),当b<0时,y随x的增大而减小.
( )
(2)函数y=-5x+3的图象经过一、二、四象限. ( )
(3)函数y=x-6上两点(2,y1),(-2,y2),则y1【例】画出函数y=x+1的图象,并根据图象回答:
(1)x为何值时,y的值为0?
(2)y为何值时,x的值为0?
(3)x为何值时,y>0?
(4)x为何值时,y随x的增大而增大?
【思路点拨】过两点作出函数图象→由图象与x轴的交点情况判断y值的正负→确定函数增减性【自主解答】过点(0,1),(-1,0)画出函数y=x+1的图象,
如图所示.
(1)当x=-1时,y=0.
(2)当y=1时,x=0.
(3)当x>-1时,y>0.
(4)x取任意实数,y都随x的增大而增大.【总结提升】函数图象或增减性确定k,b的符号
(1)由函数图象确定k,b的符号:
①确定k的符号:当函数图象过第一、三象限时,k>0;当函数图象过第二、四象限时,k<0.
②确定b的符号:当函数图象交y轴正半轴时,b>0;当函数图象交y轴负半轴时,b<0;当函数图象过原点时,b=0.(2)由函数的增减性确定k的符号:
①当y随x的增大而增大时,k>0.
②当y随x的增大而减小时,k<0.题组:一次函数的性质
1.下列函数中,y随x的增大而减小的函数
是( )
A.y=2x+8 B.y=-2+4x
C.y=-2x+8 D.y=4x
【解析】选C.A,B,D选项中的函数关系式的k值都是大于0的数,y随x的增大而增大,C选项y=-2x+8中,k=-2<0,y随x的增大而减小.2.若y=kx-4的函数值y随x的增大而增大,则k的值可能是下列
的( )
A.-4 B. C.0 D.2
【解析】选D.由题意中y随x的增大而增大,可知k>0.3.一次函数y=3x-2的函数值y随自变量x值的增大而 (填“增大”或“减小”).
【解析】∵一次函数y=3x-2中,k=3>0,
∴函数值y随自变量x值的增大而增大.
答案:增大4.直线y=2x-1沿y轴平移3个单位,则平移后直线与y轴的交点坐标为 .
【解析】把x=0代入y=2x-1得,y=-1,∴直线y=2x-1与y轴交点坐标为(0,-1),向上平移3个单位,相应点的横坐标不变,纵坐标加3,∴直线与y轴交点坐标为(0,2);向下平移3个单位,相应点的横坐标不变,纵坐标减3,∴直线与y轴交点坐标为(0,-4).综上,平移后直线与y轴的交点坐标为(0,2)或(0,-4).
答案:(0,2)或(0,-4)5.如果点P1(3,y1),P2(2,y2)在一次函数y=2x-1的图象上,则y1 y2.(填“>”“<”或“=”)
【解析】因为函数关系式为y=2x-1,所以y随x的增大而增大,又因为3>2,所以y1>y2.
答案:>6.已知关于x的一次函数y=mx+n的图象如图
所示,请化简:|n-m|-
【解析】根据题干图知,关于x的一次函数
y=mx+n的图象经过第二、四象限,所以m<0.
又因为关于x的一次函数y=mx+n的图象与y轴交于正半轴,
所以n>0,
所以|n-m|- =n-m-(-m)=n.【想一想错在哪?】直线y= +2与x轴、y轴分别交于A,B
两点,D是x轴上一点,坐标为(x,0),△ABD的面积为S.
(1)求点A和点B的坐标.
(2)当S=12时,求点D的坐标.
提示:忽略了点D在点A左侧的情况而出错.
2.一次函数性质的灵活应用.(难点)一、探究:一次函数的性质
观察函数y=3x-2,y= +1,y=-x+2,y= -1的图象.如图①所示,在函数的图象中,我们看到:当一个点在直线上
从左向右移动(自变量x从小到大)时,它的位置也在逐步从___
到___变化(函数y的值也从___变到___)——图象自左向右是
_____的,函数值y随自变量x的增大而_____.低小大上升增大高在图②中我们看到:当一个点在直线上从左向右移动(自变量x
从小到大)时,它的位置在逐步从___到___变化(函数y的值从
___变到___)——图象自左向右是_____的,函数值y随自变量x
的增大而_____.高低大小下降减小【总结】一次函数y=kx+b(k≠0)的性质:
(1)当k>0时,y随x的增大而_____,这时函数图象从左到右
_____.
(2)当k<0时,y随x的增大而_____,这时函数图象从左到右
_____.增大上升减小下降二、结合图象理解一次函数y=kx+b(k,b为常数,k≠0)的性质一、二、三一、三、四一、二、四二、三、四增大增大减小减小 (打“√”或“×”)
(1)对一次函数y=kx+b(k≠0),当b<0时,y随x的增大而减小.
( )
(2)函数y=-5x+3的图象经过一、二、四象限. ( )
(3)函数y=x-6上两点(2,y1),(-2,y2),则y1
(1)x为何值时,y的值为0?
(2)y为何值时,x的值为0?
(3)x为何值时,y>0?
(4)x为何值时,y随x的增大而增大?
【思路点拨】过两点作出函数图象→由图象与x轴的交点情况判断y值的正负→确定函数增减性【自主解答】过点(0,1),(-1,0)画出函数y=x+1的图象,
如图所示.
(1)当x=-1时,y=0.
(2)当y=1时,x=0.
(3)当x>-1时,y>0.
(4)x取任意实数,y都随x的增大而增大.【总结提升】函数图象或增减性确定k,b的符号
(1)由函数图象确定k,b的符号:
①确定k的符号:当函数图象过第一、三象限时,k>0;当函数图象过第二、四象限时,k<0.
②确定b的符号:当函数图象交y轴正半轴时,b>0;当函数图象交y轴负半轴时,b<0;当函数图象过原点时,b=0.(2)由函数的增减性确定k的符号:
①当y随x的增大而增大时,k>0.
②当y随x的增大而减小时,k<0.题组:一次函数的性质
1.下列函数中,y随x的增大而减小的函数
是( )
A.y=2x+8 B.y=-2+4x
C.y=-2x+8 D.y=4x
【解析】选C.A,B,D选项中的函数关系式的k值都是大于0的数,y随x的增大而增大,C选项y=-2x+8中,k=-2<0,y随x的增大而减小.2.若y=kx-4的函数值y随x的增大而增大,则k的值可能是下列
的( )
A.-4 B. C.0 D.2
【解析】选D.由题意中y随x的增大而增大,可知k>0.3.一次函数y=3x-2的函数值y随自变量x值的增大而 (填“增大”或“减小”).
【解析】∵一次函数y=3x-2中,k=3>0,
∴函数值y随自变量x值的增大而增大.
答案:增大4.直线y=2x-1沿y轴平移3个单位,则平移后直线与y轴的交点坐标为 .
【解析】把x=0代入y=2x-1得,y=-1,∴直线y=2x-1与y轴交点坐标为(0,-1),向上平移3个单位,相应点的横坐标不变,纵坐标加3,∴直线与y轴交点坐标为(0,2);向下平移3个单位,相应点的横坐标不变,纵坐标减3,∴直线与y轴交点坐标为(0,-4).综上,平移后直线与y轴的交点坐标为(0,2)或(0,-4).
答案:(0,2)或(0,-4)5.如果点P1(3,y1),P2(2,y2)在一次函数y=2x-1的图象上,则y1 y2.(填“>”“<”或“=”)
【解析】因为函数关系式为y=2x-1,所以y随x的增大而增大,又因为3>2,所以y1>y2.
答案:>6.已知关于x的一次函数y=mx+n的图象如图
所示,请化简:|n-m|-
【解析】根据题干图知,关于x的一次函数
y=mx+n的图象经过第二、四象限,所以m<0.
又因为关于x的一次函数y=mx+n的图象与y轴交于正半轴,
所以n>0,
所以|n-m|- =n-m-(-m)=n.【想一想错在哪?】直线y= +2与x轴、y轴分别交于A,B
两点,D是x轴上一点,坐标为(x,0),△ABD的面积为S.
(1)求点A和点B的坐标.
(2)当S=12时,求点D的坐标.
提示:忽略了点D在点A左侧的情况而出错.
