华师大版数学八年级下册17.4.1反比例函数课件(28张PPT)
文档属性
| 名称 | 华师大版数学八年级下册17.4.1反比例函数课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 719.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 09:55:25 | ||
图片预览








文档简介
课件28张PPT。17.4 反比例函数
1.反比例函数1.从具体情境和已有知识出发,讨论两个变量之间的相互关系,加深对函数概念的理解.(重点)
2.理解反比例函数的概念,会用待定系数法确定函数的关系式.(重点、难点)反比例函数:形如y=___(k为常数,k___0)的函数叫做反
比例函数,反比例函数中,自变量的取值范围是________
___________.≠不等于0的一切实数【思考】(1)关系式y= 是反比例函数吗?为什么?对自变量的取值有什么要求?
提示:不一定是.当k=0时,不是反比例函数,只有当k≠0时,是反比例函数.因为自变量x在分母的位置,故x≠0.
(2)反比例函数的关系式有什么特点?
提示:两个变量x,y的乘积为定值.【总结】(1)反比例函数的自变量x的取值范围:_____.
(2)反比例函数的三种关系式:①______.②_____.
③______(其中k≠0).x≠0xy=ky=kx-1 (打“√”或“×”)
(1)y= (k≠0)是y关于x的反比例函数. ( )
(2)反比例函数y= 的k值是 .( )
(3)xy= 不是反比例函数. ( )
(4)在实际问题中,只要两个变量的乘积是一个不为0的常数
就可以确定它们成反比例函数. ( )×√×√知识点 1 反比例函数的概念?
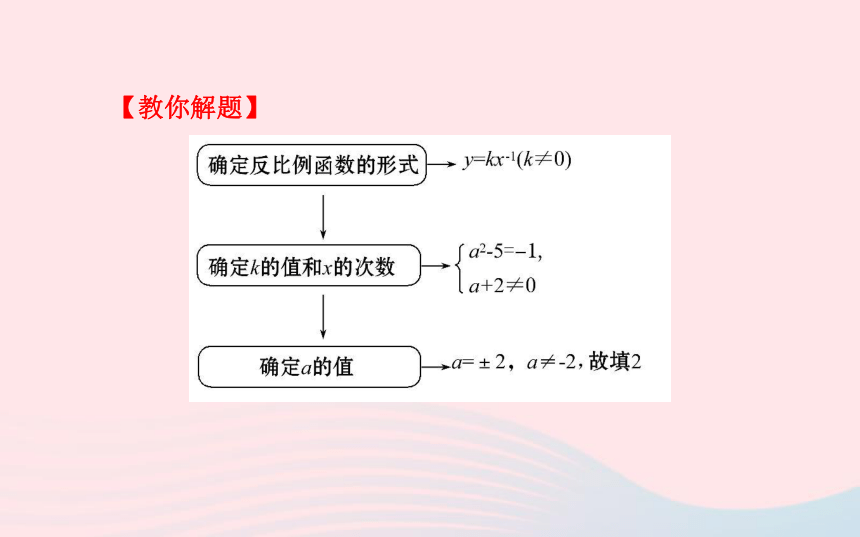
【例1】在 中,当a= 时,y是x的反比例函数.【教你解题】【总结提升】理解反比例函数y= (k≠0)的“三点注意”
(1)k是常数,且k不为0是概念的一个重要组成部分.
(2)分母x的指数为1.
(3)自变量x的取值范围是一切非零实数.知识点 2 确定反比例函数的关系式?
【例2】生物学习小组欲建一个一边长为xm,面积是30m2的三角形生物养殖区.若这条边上的高为ym,
(1)求y关于x的函数关系式及自变量x的取值范围.
(2)y关于x的函数是不是反比例函数?【解题探究】(1)一边长为x m,这条边上的高为y m的三角形的面积为30 m2,如何确定关系式?
提示:根据三角形的面积公式S= ×底×高,可得
xy=30.(2)怎样根据(1)写出y关于x的函数关系式?如何确定自变量x的取值范围?
提示: 因为x为三角形的一边长,故x>0.(3)如何判断(2)中的y与x的函数关系式是否为反比例函数?
提示:判断是否为反比例函数时,主要看是否满足y=
(k为常数,k≠0)的形式,由y= 可知,y是x的反比例函数.【总结提升】确定反比例函数关系式的“四字诀”题组一:反比例函数的概念
1.下列函数中,是反比例函数的是( )
A.y= B.y=
C.y=x D.y=
【解析】选B. y= 和y=x都是正比例函数,y= 中分母x
的指数为2,y= 是反比例函数,比例系数为2.某农场的粮食总产量为1 500吨,设该农场人数为x人,平均每人占有粮食为y吨,则y与x之间的函数关系是( )
A.正比例函数 B.反比例函数
C.一次函数 D.无法确定
【解析】选B.根据题意得xy=1 500,根据实际意义有x,
y应大于0,所以y= (x>0,y>0).3.若y=-2xm-1是反比例函数,则m的值是______.
【解析】反比例函数y= 可写成y=kx-1的形式,x的次数
为-1,即m-1=-1,则m=0.
答案:04.已知反比例函数y= ,当y=6时,x=______.
【解析】将y=6代入y= 得,6= ,所以x= .
答案: 5.已知函数y=(m2-3) 是反比例函数,则m=____.
【解析】由题意知,x的次数m2-5=-1,则m2=4,
解得m=±2,又m2-3≠0,
即m≠± ,因此m=±2.
答案:±2题组二:确定反比例函数的关系式
1.某玩具厂计划生产一种玩具熊猫,已知每只玩具熊猫的成本为y元,若该厂每月生产x只(x取正整数),这个月的总成本为
5 000元,则y与x之间满足的关系为( )
【解析】选C.由题意得:y与x之间满足的关系为xy=5 000,
即2.在一个可以改变容积的密闭容器内,装有一定质量的某种气体,当改变容积V时,气体的密度ρ也随之改变.在一定范围内,密度ρ是容积V的反比例函数.当容积为5 m3时,密度是1.4 kg/m3,则ρ与V的函数关系式为_______.【解析】∵密度ρ是容积V的反比例函数,∴设ρ=
∵V=5时,ρ=1.4,
∴k=1.4×5=7,∴ρ=
答案:ρ=【归纳整合】反比例函数关系式的确定方法
1.常用方法:待定系数法,选定一组变量的值代入y= (k≠0)中,求出k的值即可确定函数关系式.
2.借助一些体积、面积、压强等公式确定反比例函数关系式.另外也会用到整体思想来确定反比例函数关系式.3.已知y与x成反比例,且当x=-1时,y=5,则当x=20时,y=________.
【解析】设y= ,将x=-1,y=5代入y= ,得k=-5,所以
y=- ,当x=20时,y=
答案:4.已知一个长方体的体积是100 cm3,它的长是y cm,宽是
5 cm,高是x cm.
(1)写出用高表示长的函数关系式.
(2)写出自变量x的取值范围.
(3)当x=3时,求y的值.
【解析】(1)根据长方体的体积可知5xy=100,即y=
(2)x>0.(3)当x=3时,y=5.水池中有水若干吨,若单开一个出水口,水流速度v与全池水放完所用时间t如表:求出放完池中水用时间t(h)与放水速度v(t/h)之间的函数关系,这是一个反比例函数吗?【解析】∵水池的容量=10×1=10,
∴放完池中水用时t=
符合反比例函数的一般形式,
∴是一个反比例函数.【想一想错在哪?】若y与x-2成反比例,且当x=-1时,y=3,求y与x之间的函数关系,y与x是反比例函数吗?提示:y与x-2成反比例,而y与x之间不是反比例关系.
1.反比例函数1.从具体情境和已有知识出发,讨论两个变量之间的相互关系,加深对函数概念的理解.(重点)
2.理解反比例函数的概念,会用待定系数法确定函数的关系式.(重点、难点)反比例函数:形如y=___(k为常数,k___0)的函数叫做反
比例函数,反比例函数中,自变量的取值范围是________
___________.≠不等于0的一切实数【思考】(1)关系式y= 是反比例函数吗?为什么?对自变量的取值有什么要求?
提示:不一定是.当k=0时,不是反比例函数,只有当k≠0时,是反比例函数.因为自变量x在分母的位置,故x≠0.
(2)反比例函数的关系式有什么特点?
提示:两个变量x,y的乘积为定值.【总结】(1)反比例函数的自变量x的取值范围:_____.
(2)反比例函数的三种关系式:①______.②_____.
③______(其中k≠0).x≠0xy=ky=kx-1 (打“√”或“×”)
(1)y= (k≠0)是y关于x的反比例函数. ( )
(2)反比例函数y= 的k值是 .( )
(3)xy= 不是反比例函数. ( )
(4)在实际问题中,只要两个变量的乘积是一个不为0的常数
就可以确定它们成反比例函数. ( )×√×√知识点 1 反比例函数的概念?
【例1】在 中,当a= 时,y是x的反比例函数.【教你解题】【总结提升】理解反比例函数y= (k≠0)的“三点注意”
(1)k是常数,且k不为0是概念的一个重要组成部分.
(2)分母x的指数为1.
(3)自变量x的取值范围是一切非零实数.知识点 2 确定反比例函数的关系式?
【例2】生物学习小组欲建一个一边长为xm,面积是30m2的三角形生物养殖区.若这条边上的高为ym,
(1)求y关于x的函数关系式及自变量x的取值范围.
(2)y关于x的函数是不是反比例函数?【解题探究】(1)一边长为x m,这条边上的高为y m的三角形的面积为30 m2,如何确定关系式?
提示:根据三角形的面积公式S= ×底×高,可得
xy=30.(2)怎样根据(1)写出y关于x的函数关系式?如何确定自变量x的取值范围?
提示: 因为x为三角形的一边长,故x>0.(3)如何判断(2)中的y与x的函数关系式是否为反比例函数?
提示:判断是否为反比例函数时,主要看是否满足y=
(k为常数,k≠0)的形式,由y= 可知,y是x的反比例函数.【总结提升】确定反比例函数关系式的“四字诀”题组一:反比例函数的概念
1.下列函数中,是反比例函数的是( )
A.y= B.y=
C.y=x D.y=
【解析】选B. y= 和y=x都是正比例函数,y= 中分母x
的指数为2,y= 是反比例函数,比例系数为2.某农场的粮食总产量为1 500吨,设该农场人数为x人,平均每人占有粮食为y吨,则y与x之间的函数关系是( )
A.正比例函数 B.反比例函数
C.一次函数 D.无法确定
【解析】选B.根据题意得xy=1 500,根据实际意义有x,
y应大于0,所以y= (x>0,y>0).3.若y=-2xm-1是反比例函数,则m的值是______.
【解析】反比例函数y= 可写成y=kx-1的形式,x的次数
为-1,即m-1=-1,则m=0.
答案:04.已知反比例函数y= ,当y=6时,x=______.
【解析】将y=6代入y= 得,6= ,所以x= .
答案: 5.已知函数y=(m2-3) 是反比例函数,则m=____.
【解析】由题意知,x的次数m2-5=-1,则m2=4,
解得m=±2,又m2-3≠0,
即m≠± ,因此m=±2.
答案:±2题组二:确定反比例函数的关系式
1.某玩具厂计划生产一种玩具熊猫,已知每只玩具熊猫的成本为y元,若该厂每月生产x只(x取正整数),这个月的总成本为
5 000元,则y与x之间满足的关系为( )
【解析】选C.由题意得:y与x之间满足的关系为xy=5 000,
即2.在一个可以改变容积的密闭容器内,装有一定质量的某种气体,当改变容积V时,气体的密度ρ也随之改变.在一定范围内,密度ρ是容积V的反比例函数.当容积为5 m3时,密度是1.4 kg/m3,则ρ与V的函数关系式为_______.【解析】∵密度ρ是容积V的反比例函数,∴设ρ=
∵V=5时,ρ=1.4,
∴k=1.4×5=7,∴ρ=
答案:ρ=【归纳整合】反比例函数关系式的确定方法
1.常用方法:待定系数法,选定一组变量的值代入y= (k≠0)中,求出k的值即可确定函数关系式.
2.借助一些体积、面积、压强等公式确定反比例函数关系式.另外也会用到整体思想来确定反比例函数关系式.3.已知y与x成反比例,且当x=-1时,y=5,则当x=20时,y=________.
【解析】设y= ,将x=-1,y=5代入y= ,得k=-5,所以
y=- ,当x=20时,y=
答案:4.已知一个长方体的体积是100 cm3,它的长是y cm,宽是
5 cm,高是x cm.
(1)写出用高表示长的函数关系式.
(2)写出自变量x的取值范围.
(3)当x=3时,求y的值.
【解析】(1)根据长方体的体积可知5xy=100,即y=
(2)x>0.(3)当x=3时,y=5.水池中有水若干吨,若单开一个出水口,水流速度v与全池水放完所用时间t如表:求出放完池中水用时间t(h)与放水速度v(t/h)之间的函数关系,这是一个反比例函数吗?【解析】∵水池的容量=10×1=10,
∴放完池中水用时t=
符合反比例函数的一般形式,
∴是一个反比例函数.【想一想错在哪?】若y与x-2成反比例,且当x=-1时,y=3,求y与x之间的函数关系,y与x是反比例函数吗?提示:y与x-2成反比例,而y与x之间不是反比例关系.
