华师大版数学八年级下册17.3.1一次函数课件(共26张PPT)
文档属性
| 名称 | 华师大版数学八年级下册17.3.1一次函数课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 618.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 10:02:32 | ||
图片预览








文档简介
课件26张PPT。 17.3 一次函数
1.一次函数1.理解一次函数和正比例函数的概念,以及它们之间的联系.(重点)
2.能根据所给条件写出简单的一次函数关系式.
3.经历一般规律的探索过程、发展学生的抽象思维能力.
4.通过由已知信息写一次函数关系式的过程,发展学生的数学应用能力.(难点)汽车离开A站4km,再以40km/h的平均速度行驶了xh,那么汽车离开A站的距离y(km)与时间x(h)之间的关系是怎样的?【思考】(1)上面问题中的相等关系是什么?
提示:路程=速度×时间,离开A站的距离=4+又行驶的路程.
(2)如何用关系式表示y与x的关系?是正比例函数吗?
提示:根据(1)的相等关系可得,y=40x+4(x≥0).从关系式上来看,不是正比例函数,比正比例函数多了一个常数项.
(3)这种函数关系是什么函数?怎样用关系式表示一般形式?
提示:这种函数是一次函数,一般形式为y=kx+b(k,b是常数,k≠0).【总结】(1)一次函数的定义:形如_______(k,b是常数,
k≠0)的函数.
(2)一次函数与正比例函数的关系:如果一次函数y=kx+b(k,
b是常数,k≠0)中的常数b=__,关系式变为y=kx(k是常数,
k≠0),即正比例函数.y=kx+b0 (打“√”或“×”)
(1)正比例函数一定是一次函数. ( )
(2)一次函数一定是正比例函数.( )
(3)y= +3是一次函数.( )
(4)一次函数y= -3,其中k=5,b=-3.( )√×√×知识点 1一次函数、正比例函数的判别
【例1】下列函数中,哪些是一次函数?哪些是正比例函数?
(1)y= (2)y=1-x.
(3)y=x2.(4)y=2+2(x-1).
【思路点拨】根据一次函数与正比例函数的定义进行判断.【自主解答】(1)y= 不能化为y=kx+b(k,b是常数,k≠0)
的形式,所以y不是x的一次函数,也不是x的正比例函数.
(2)y=1-x=-x+1,其中k=-1,b=1,所以y是x的一次函数,但
不是x的正比例函数.
(3)y=x2的自变量次数不是1,所以y不是x的一次函数,也不
是x的正比例函数.
(4)y=2+2(x-1)=2+2x-2=2x,所以y是x的一次函数,也是x的
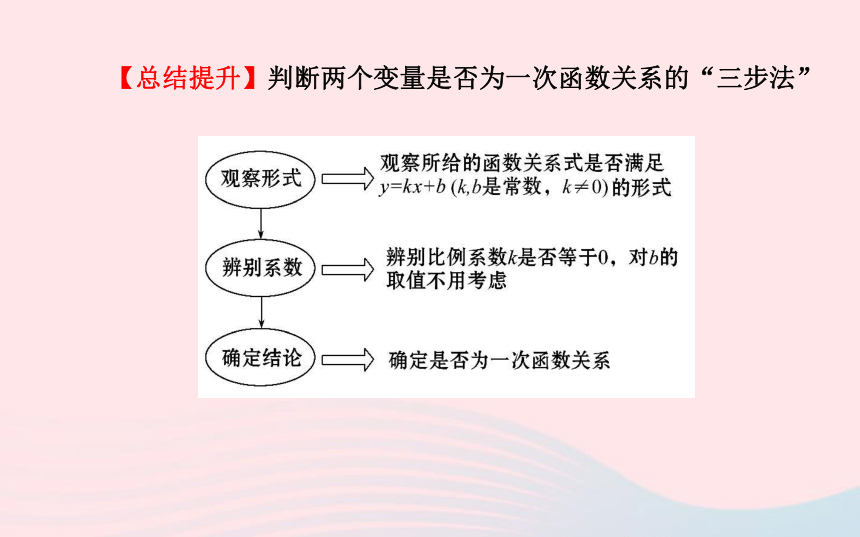
正比例函数.【总结提升】判断两个变量是否为一次函数关系的“三步法”知识点 2 列一次函数关系式
【例2】写出下列各题中y与x之间的关系式,并判断y是否为x的一次函数?是否为正比例函数?
(1)三角形的一边为8 cm,三角形的面积y(cm2)与此边上的高x(cm)的关系.
(2)某小汽车的油箱可装汽油30 L,原来装有汽油10 L,现在再加汽油x L,如果每升汽油7.5元,油箱内汽油的总价y(元)与x(L)之间的关系.【思路点拨】先确定y与x之间的关系式,再判断y与x的函数关系.
【自主解答】(1)由三角形的面积公式,得y=4x,y是x的一次函数,也是x的正比例函数.
(2)由题意得y=10×7.5+7.5x=7.5x+75(0<x≤20),y是x的一次函数,但不是正比例函数.【总结提升】在实际问题中列一次函数关系式的方法
(1)列实际问题中的一次函数关系式和列方程解应用题的思路相同,只是书写格式不同.
(2)首先要认真审题,找出等量关系,用字母表示问题中的变量,然后根据题意列出一次函数关系式.
(3)根据实际问题的实际意义,写出自变量的取值范围.题组一:一次函数、正比例函数的判别
1.下列函数:①y=x;②y= ③y= ④y=2x+1,其中一次
函数的个数是( )
A.1 B.2 C.3 D.4【解析】选C.一次函数y=kx+b的定义条件是:k,b为常数,
k≠0,自变量次数为1.
①y=x是一次函数;
②y= 是一次函数;
③y= 自变量次数不为1,故不是一次函数;
④y=2x+1是一次函数.2.函数y=(2-a)x+b-1是正比例函数的条件是( )
A.a≠2
B.b=1
C.a≠2且b=1
D.a,b可取任意实数
【解析】选C.根据正比例函数的意义得出:2-a≠0,b-1=0,解得a≠2,b=1.3.若函数y=(m-1)x|m|+2是一次函数,则( )
A.m=±1 B.m=-1
C.m=1 D.m≠-1
【解析】选B.根据题意得:m-1≠0,|m|=1,
解得m=-1.4.在一次函数y=-2(x+1)+x中,比例系数k为 ,常数项b为 .
【解析】化简一次函数为y=-2(x+1)+x=-x-2,
故其比例系数k为-1,
常数项b为-2.
答案:-1 -25.已知函数y=(m-1)xm2+1是一次函数,则m=_______.
【解析】∵一次函数y=kx+b的定义条件是:
k,b为常数,k≠0,自变量次数为1,
∴m-1≠0,m2=1, 解得m=-1.
答案:-16.已知函数y=(m-10)x+1-2m.
(1)m为何值时,这个函数是一次函数?
(2)m为何值时,这个函数是正比例函数?
【解析】(1)根据一次函数的定义可得:m-10≠0,
∴m≠10时,这个函数是一次函数.
(2)根据正比例函数的定义,
可得:m-10≠0且1-2m=0,
∴m= 时,这个函数是正比例函数.题组二:列一次函数关系式
1.下列问题中,变量y与x成一次函数关系的是( )
A.路程一定时,时间y和速度x的关系
B.长10米的铁丝折成长为y,宽为x的长方形
C.圆的面积y与它的半径x
D.斜边长为5的直角三角形的直角边y和x【解析】选B.A,设路程是s,则根据题意知,y= 不是一
次函数关系.
B,根据题意,知10=2(x+y),即y=-x+5,符合一次函数的定
义.
C,根据题意,知y=πx2,自变量次数为2,不符合一次函数
的定义.
D,根据题意,知x2+y2=25,不符合一次函数的定义.2.甲乙两地相距200 km,一辆客车从甲地驶往乙地,客车行驶的平均速度为80 km/h.x h后客车距乙地y km,则y与x之间的函数关系式为( )
A.y=80x-200 B.y=-80x-200
C.y=80x+200 D.y=-80x+200
【解析】选D.由题意得y=200-80x=-80x+200.3.为庆祝建校30周年,学校组织文艺汇演,八年级排练队形为10排,第一排20人,后面每排比前排多2人,则每排人数y与这排的排数x之间的函数关系式为________.
【解析】根据题意得y=20+(x-1)×2=20+2(x-1)=2x+18 (1≤x≤10,且x为整数).
答案:y=2x+18(1≤x≤10,且x为整数)4.一个长为120m,宽为100m的矩形场地要扩建成一个正方
形场地,设长增加xm,宽增加ym,则y与x的函数关系式
是 ,自变量的取值范围是 ,且y是x的
函数.
【解析】依题意有120+x=100+y,
则y=x+20,
x不能是负数,所以x≥0,符合一次函数的一般形式.
答案:y=x+20 x≥0 一次5.某汽车加油站储油45000L,每天给汽车加油1 500 L,那么储油量y(L)与加油x(天)之间的关系式是什么?并指出自变量的取值范围.
【解析】根据题意得储油量y(L)与加油x(天)之间的关系式是:y=45000-1500x,
∵1500x≤45000,x≥0,
∴0≤x≤30,
即y=45000-1500x(0≤x≤30).【想一想错在哪?】已知函数y=(k+3)x2k-1+4x-5是一次函数,试求k的值.
提示:漏情况而出现答案不全致错.
1.一次函数1.理解一次函数和正比例函数的概念,以及它们之间的联系.(重点)
2.能根据所给条件写出简单的一次函数关系式.
3.经历一般规律的探索过程、发展学生的抽象思维能力.
4.通过由已知信息写一次函数关系式的过程,发展学生的数学应用能力.(难点)汽车离开A站4km,再以40km/h的平均速度行驶了xh,那么汽车离开A站的距离y(km)与时间x(h)之间的关系是怎样的?【思考】(1)上面问题中的相等关系是什么?
提示:路程=速度×时间,离开A站的距离=4+又行驶的路程.
(2)如何用关系式表示y与x的关系?是正比例函数吗?
提示:根据(1)的相等关系可得,y=40x+4(x≥0).从关系式上来看,不是正比例函数,比正比例函数多了一个常数项.
(3)这种函数关系是什么函数?怎样用关系式表示一般形式?
提示:这种函数是一次函数,一般形式为y=kx+b(k,b是常数,k≠0).【总结】(1)一次函数的定义:形如_______(k,b是常数,
k≠0)的函数.
(2)一次函数与正比例函数的关系:如果一次函数y=kx+b(k,
b是常数,k≠0)中的常数b=__,关系式变为y=kx(k是常数,
k≠0),即正比例函数.y=kx+b0 (打“√”或“×”)
(1)正比例函数一定是一次函数. ( )
(2)一次函数一定是正比例函数.( )
(3)y= +3是一次函数.( )
(4)一次函数y= -3,其中k=5,b=-3.( )√×√×知识点 1一次函数、正比例函数的判别
【例1】下列函数中,哪些是一次函数?哪些是正比例函数?
(1)y= (2)y=1-x.
(3)y=x2.(4)y=2+2(x-1).
【思路点拨】根据一次函数与正比例函数的定义进行判断.【自主解答】(1)y= 不能化为y=kx+b(k,b是常数,k≠0)
的形式,所以y不是x的一次函数,也不是x的正比例函数.
(2)y=1-x=-x+1,其中k=-1,b=1,所以y是x的一次函数,但
不是x的正比例函数.
(3)y=x2的自变量次数不是1,所以y不是x的一次函数,也不
是x的正比例函数.
(4)y=2+2(x-1)=2+2x-2=2x,所以y是x的一次函数,也是x的
正比例函数.【总结提升】判断两个变量是否为一次函数关系的“三步法”知识点 2 列一次函数关系式
【例2】写出下列各题中y与x之间的关系式,并判断y是否为x的一次函数?是否为正比例函数?
(1)三角形的一边为8 cm,三角形的面积y(cm2)与此边上的高x(cm)的关系.
(2)某小汽车的油箱可装汽油30 L,原来装有汽油10 L,现在再加汽油x L,如果每升汽油7.5元,油箱内汽油的总价y(元)与x(L)之间的关系.【思路点拨】先确定y与x之间的关系式,再判断y与x的函数关系.
【自主解答】(1)由三角形的面积公式,得y=4x,y是x的一次函数,也是x的正比例函数.
(2)由题意得y=10×7.5+7.5x=7.5x+75(0<x≤20),y是x的一次函数,但不是正比例函数.【总结提升】在实际问题中列一次函数关系式的方法
(1)列实际问题中的一次函数关系式和列方程解应用题的思路相同,只是书写格式不同.
(2)首先要认真审题,找出等量关系,用字母表示问题中的变量,然后根据题意列出一次函数关系式.
(3)根据实际问题的实际意义,写出自变量的取值范围.题组一:一次函数、正比例函数的判别
1.下列函数:①y=x;②y= ③y= ④y=2x+1,其中一次
函数的个数是( )
A.1 B.2 C.3 D.4【解析】选C.一次函数y=kx+b的定义条件是:k,b为常数,
k≠0,自变量次数为1.
①y=x是一次函数;
②y= 是一次函数;
③y= 自变量次数不为1,故不是一次函数;
④y=2x+1是一次函数.2.函数y=(2-a)x+b-1是正比例函数的条件是( )
A.a≠2
B.b=1
C.a≠2且b=1
D.a,b可取任意实数
【解析】选C.根据正比例函数的意义得出:2-a≠0,b-1=0,解得a≠2,b=1.3.若函数y=(m-1)x|m|+2是一次函数,则( )
A.m=±1 B.m=-1
C.m=1 D.m≠-1
【解析】选B.根据题意得:m-1≠0,|m|=1,
解得m=-1.4.在一次函数y=-2(x+1)+x中,比例系数k为 ,常数项b为 .
【解析】化简一次函数为y=-2(x+1)+x=-x-2,
故其比例系数k为-1,
常数项b为-2.
答案:-1 -25.已知函数y=(m-1)xm2+1是一次函数,则m=_______.
【解析】∵一次函数y=kx+b的定义条件是:
k,b为常数,k≠0,自变量次数为1,
∴m-1≠0,m2=1, 解得m=-1.
答案:-16.已知函数y=(m-10)x+1-2m.
(1)m为何值时,这个函数是一次函数?
(2)m为何值时,这个函数是正比例函数?
【解析】(1)根据一次函数的定义可得:m-10≠0,
∴m≠10时,这个函数是一次函数.
(2)根据正比例函数的定义,
可得:m-10≠0且1-2m=0,
∴m= 时,这个函数是正比例函数.题组二:列一次函数关系式
1.下列问题中,变量y与x成一次函数关系的是( )
A.路程一定时,时间y和速度x的关系
B.长10米的铁丝折成长为y,宽为x的长方形
C.圆的面积y与它的半径x
D.斜边长为5的直角三角形的直角边y和x【解析】选B.A,设路程是s,则根据题意知,y= 不是一
次函数关系.
B,根据题意,知10=2(x+y),即y=-x+5,符合一次函数的定
义.
C,根据题意,知y=πx2,自变量次数为2,不符合一次函数
的定义.
D,根据题意,知x2+y2=25,不符合一次函数的定义.2.甲乙两地相距200 km,一辆客车从甲地驶往乙地,客车行驶的平均速度为80 km/h.x h后客车距乙地y km,则y与x之间的函数关系式为( )
A.y=80x-200 B.y=-80x-200
C.y=80x+200 D.y=-80x+200
【解析】选D.由题意得y=200-80x=-80x+200.3.为庆祝建校30周年,学校组织文艺汇演,八年级排练队形为10排,第一排20人,后面每排比前排多2人,则每排人数y与这排的排数x之间的函数关系式为________.
【解析】根据题意得y=20+(x-1)×2=20+2(x-1)=2x+18 (1≤x≤10,且x为整数).
答案:y=2x+18(1≤x≤10,且x为整数)4.一个长为120m,宽为100m的矩形场地要扩建成一个正方
形场地,设长增加xm,宽增加ym,则y与x的函数关系式
是 ,自变量的取值范围是 ,且y是x的
函数.
【解析】依题意有120+x=100+y,
则y=x+20,
x不能是负数,所以x≥0,符合一次函数的一般形式.
答案:y=x+20 x≥0 一次5.某汽车加油站储油45000L,每天给汽车加油1 500 L,那么储油量y(L)与加油x(天)之间的关系式是什么?并指出自变量的取值范围.
【解析】根据题意得储油量y(L)与加油x(天)之间的关系式是:y=45000-1500x,
∵1500x≤45000,x≥0,
∴0≤x≤30,
即y=45000-1500x(0≤x≤30).【想一想错在哪?】已知函数y=(k+3)x2k-1+4x-5是一次函数,试求k的值.
提示:漏情况而出现答案不全致错.
