华师大版数学八年级下册17.3.2一次函数的图象课件(34张PPT)
文档属性
| 名称 | 华师大版数学八年级下册17.3.2一次函数的图象课件(34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 671.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 10:03:03 | ||
图片预览










文档简介
课件34张PPT。2.一次函数的图象1.经历探究画一次函数图象的过程,了解一次函数、正比例函数的图象特征.(重点)
2.会用两点法画一次函数、正比例函数的图象.(重点)
3.了解直线y=kx+b(k,b是常数,k≠0)中k,b的取值与直线的位置关系.(难点)
4.能正确画出实际问题中的一次函数图象.(难点)用描点法在同一坐标系内画函数y=2x,y=2x+3和y=-x+3的图象:
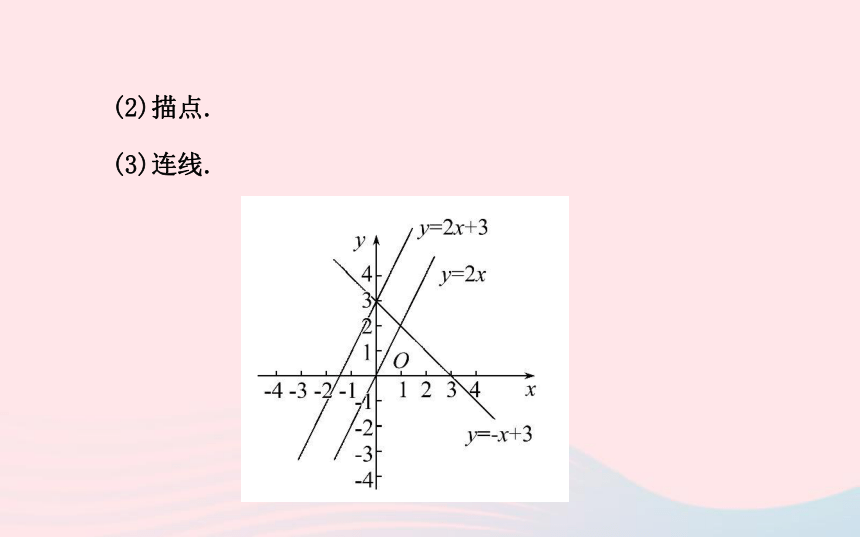
(1)列表:(2)描点.
(3)连线.【思考】(1)这三个函数的共同点是它们的图象都是_____.
(2)函数y=2x和y=2x+3的位置关系如何?
提示:直线y=2x和y=2x+3互相平行.
(3)如何移动直线y=2x才能得到直线y=2x+3?
提示:把直线y=2x向上平移3个单位即可得到
直线y=2x+3.
(4)函数y=2x+3和y=-x+3的图象都经过点_______.直线(0,3)【总结】(1)一次函数y=kx+b(k≠0)的图象是一条_____.特别
地,正比例函数y=kx(k≠0)的图象是经过___________的一条
直线.
(2)一次函数y=kx+b(k,b是常数,k≠0)的图象可以看作由直
线y=kx(k是常数,k≠0)平移|b|个单位而得到(当b>0时,向
___平移,当b<0时,向___平移).直线原点(0,0)上下(3)对于直线y=kx+b(k,b是常数,k≠0):
当k>0,b>0时,直线经过第___________象限;
当k>0,b<0时,直线经过第___________象限;
当k<0,b>0时,直线经过第___________象限;
当k<0,b<0时,直线经过第___________象限.一、二、三一、三、四一、二、四二、三、四 (打“√”或“×”)
(1)一次函数y=kx+b的图象经过点 ( )
(2)画一次函数的图象时只要能确定两点即可. ( )
(3)直线y=6x-3是由直线y=6x向上平移3个单位得到的.( )
(4)直线y=-2x+5与y轴的交点坐标为(0,5).( )
(5)直线y=-3x-2经过第二、三、四象限.( )×√×√√知识点 1 一次函数图象的画法
【例1】在同一平面直角坐标系中画出下列函数的图象.观察图象,你有什么发现?
(1)y=x+2;(2)y=x-2;(3)y=-x;(4)y=-x+2.
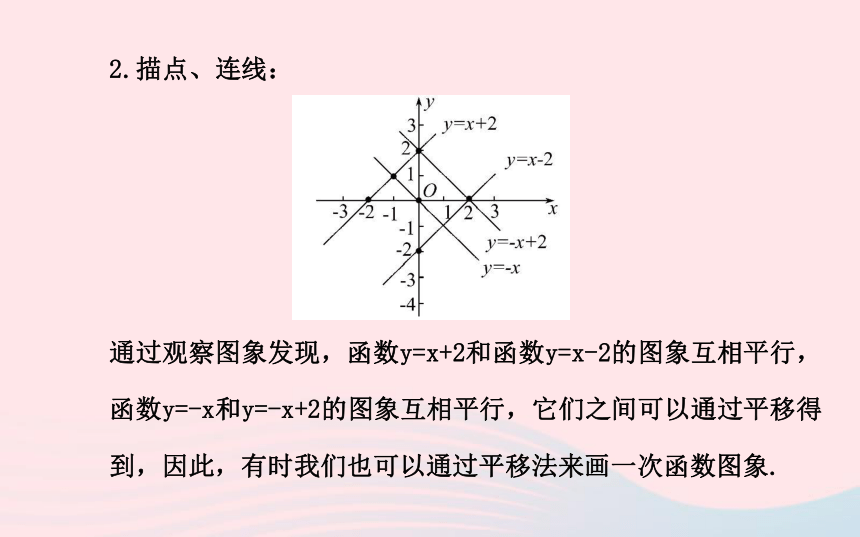
【思路点拨】列表、描点、连线画出图象.【自主解答】1.列表: 2.描点、连线:
通过观察图象发现,函数y=x+2和函数y=x-2的图象互相平行,函数y=-x和y=-x+2的图象互相平行,它们之间可以通过平移得到,因此,有时我们也可以通过平移法来画一次函数图象.【总结提升】认识一次函数图象的两个角度
1.函数图象的形状.
一次函数y=kx+b(k,b是常数,k≠0,b≠0)的图象是一条经过
(0,b)和 两点的直线.当直线经过原点时(即b=0),这
时函数是正比例函数.2.函数图象的位置.
(1)直线y=kx+b(k,b是常数,k≠0)与直线y=kx(k是常数,k≠0)的位置关系:
①直线y=kx+b(k,b是常数,k≠0)平行于直线y=kx(k是常数,k≠0);
②当b>0时,把直线y=kx向上平移b个单位长度,可得直线y=kx+b;当b<0时,把直线y=kx向下平移|b|个单位长度,可得直线y=kx+b.(2)直线y1=k1x+b1与直线y2=k2x+b2(k1≠0,k2≠0)的位置关
系:
①k1≠k2?y1与y2相交;
② y1与y2相交于y轴上的同一点;
? y1与y2平行;
y1与y2重合.知识点 2 一次函数图象位置与k与b的关系
【例2】关于x的一次函数y=kx+k2+1的图象可能正确的是( )【解题探究】选__.函数y=kx+k2+1的图象与y轴交于点
_________,∵k2+1>0,∴图象与y轴的交点在y轴的_______上.
分析函数图象只有选项__满足题意,故选__.(0,k2+1)正半轴CCC【总结提升】一次函数y=kx+b图象位置的四种情况
(1)k>0,b>0?函数y=kx+b的图象经过第一、二、三象限.
(2)k>0,b<0?函数y=kx+b的图象经过第一、三、四象限.
(3)k<0,b>0?函数y=kx+b的图象经过第一、二、四象限.
(4)k<0,b<0?函数y=kx+b的图象经过第二、三、四象限.题组一:一次函数图象的画法
1.下列各点在正比例函数y=-10x的图象上的是( )
A.(1,10) B.(2,-5)
C.(-1,10) D.(-2,-5)
【解析】选C.当x=1时,y=-10x=-10×1=-10,
当x=2时,y=-20,当x=-1时,y=10,当x=-2时,y=20.2.直线y=kx-1一定经过点( )
A.(1,0) B.(1,k) C.(0,k) D.(0,-1)
【解析】选D.∵直线y=kx-1中b=-1,
∴此直线一定与y轴相交于(0,-1)点,
∴此直线一定过点(0,-1).3.将函数y=-3x+3的图象向上平移2个单位,得到函数的图象是 .
【解析】原直线的k=-3,b=3;向上平移2个单位得到了新直线,那么新直线的k=-3,b=3+2=5.∴新直线的关系式为
y=-3x+5.
答案:y=-3x+54.在正比例函数y=-3mx中,函数y的值随x值的增大而增大,则P(m,5)在第 象限.
【解析】∵正比例函数y=-3mx中,函数y的值随x值的增大而增大,
∴-3m>0,解得m<0,∴点P(m,5)在第二象限.
答案:二5.某学校的复印任务原来由甲复印社承接,其收费y(元)与复印页数x(页)的关系如表:(1)若收费y(元)与复印页数x(页)满足学过的某一函数关系,求函数的关系式.
(2)现在乙复印社表示:若学校先按每月付给200元的承包费,则可按每页0.15元收费.则乙复印社每月收费y(元)与复印页数x(页)的函数关系为 .(3)在给出的坐标系内画出(1)(2)中的函数图象,并回答每月复印页数在1200左右应选择哪个复印社?【解析】(1)根据题意,收费y(元)与复印页数x(页)的关系式为y=0.4x(x≥0).
(2)乙复印社每月收费y(元)由承包费和复印费两部分组成,所以乙复印社每月收费y(元)与复印页数x(页)的函数关系为y=0.15x+200(x≥0).(3)作图:
由图象可知,当每月复印页数在1200左右时,选择乙复印社更合算.题组二:一次函数图象位置与k与b的关系
1.若实数a,b,c满足a+b+c=0,且a【解析】选A.实数a,b,c满足a+b+c=0,且a得a<0,c>0,所以函数y=ax+c的图象可能是选项A中的图象.2.关于一次函数y=-x+1的图象,下列所画正确的是( )
【解析】选C.由题意得:函数的k=-1,b=1,
∴函数为减函数,且与y轴的交点在y轴的正半轴,
结合选项可得C符合题意.3.一次函数y=x-2的图象不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】选B.一次函数y=x-2,
∵k=1>0,∴函数图象经过第一、三象限.
∵b=-2<0,∴函数图象与y轴负半轴相交,经过第三、四象限,
∴函数图象不经过第二象限.4.如图,一次函数
y=(m-2)x-1的图象经过第二、三、四
象限,则m的取值范围是( )
A.m>0 B.m<0
C.m>2 D.m<2
【解析】选D.由图象知一次函数y=(m-2)x-1的图象经过第二、三、四象限得m-2<0,解得m<2.5.若点(m,n)在函数y=2x+1的图象上,则2m-n的值是( )
A.2 B.-2 C.1 D.-1
【解析】选D.把点(m,n)代入函数关系式得n=2m+1,
∴2m-n=-1.6.已知一次函数y=(6+3m)x+n-4.
(1)当m,n为何值时,函数的图象过原点?
(2)当m,n满足什么条件时,函数的图象经过第一、二、三象限?【解析】(1)∵一次函数y=(6+3m)x+n-4的图象过原点,
∴6+3m≠0,且n-4=0,
解得,m≠-2,n=4.
(2)∵该函数的图象经过第一、二、三象限,
∴6+3m>0,且n-4>0,
解得m>-2,n>4.【想一想错在哪?】 已知一次函数y=(k-2)x+k不经过第三 象限,求k的取值范围.
提示:忽略正比例函数是特殊的一次函数的情形.
2.会用两点法画一次函数、正比例函数的图象.(重点)
3.了解直线y=kx+b(k,b是常数,k≠0)中k,b的取值与直线的位置关系.(难点)
4.能正确画出实际问题中的一次函数图象.(难点)用描点法在同一坐标系内画函数y=2x,y=2x+3和y=-x+3的图象:
(1)列表:(2)描点.
(3)连线.【思考】(1)这三个函数的共同点是它们的图象都是_____.
(2)函数y=2x和y=2x+3的位置关系如何?
提示:直线y=2x和y=2x+3互相平行.
(3)如何移动直线y=2x才能得到直线y=2x+3?
提示:把直线y=2x向上平移3个单位即可得到
直线y=2x+3.
(4)函数y=2x+3和y=-x+3的图象都经过点_______.直线(0,3)【总结】(1)一次函数y=kx+b(k≠0)的图象是一条_____.特别
地,正比例函数y=kx(k≠0)的图象是经过___________的一条
直线.
(2)一次函数y=kx+b(k,b是常数,k≠0)的图象可以看作由直
线y=kx(k是常数,k≠0)平移|b|个单位而得到(当b>0时,向
___平移,当b<0时,向___平移).直线原点(0,0)上下(3)对于直线y=kx+b(k,b是常数,k≠0):
当k>0,b>0时,直线经过第___________象限;
当k>0,b<0时,直线经过第___________象限;
当k<0,b>0时,直线经过第___________象限;
当k<0,b<0时,直线经过第___________象限.一、二、三一、三、四一、二、四二、三、四 (打“√”或“×”)
(1)一次函数y=kx+b的图象经过点 ( )
(2)画一次函数的图象时只要能确定两点即可. ( )
(3)直线y=6x-3是由直线y=6x向上平移3个单位得到的.( )
(4)直线y=-2x+5与y轴的交点坐标为(0,5).( )
(5)直线y=-3x-2经过第二、三、四象限.( )×√×√√知识点 1 一次函数图象的画法
【例1】在同一平面直角坐标系中画出下列函数的图象.观察图象,你有什么发现?
(1)y=x+2;(2)y=x-2;(3)y=-x;(4)y=-x+2.
【思路点拨】列表、描点、连线画出图象.【自主解答】1.列表: 2.描点、连线:
通过观察图象发现,函数y=x+2和函数y=x-2的图象互相平行,函数y=-x和y=-x+2的图象互相平行,它们之间可以通过平移得到,因此,有时我们也可以通过平移法来画一次函数图象.【总结提升】认识一次函数图象的两个角度
1.函数图象的形状.
一次函数y=kx+b(k,b是常数,k≠0,b≠0)的图象是一条经过
(0,b)和 两点的直线.当直线经过原点时(即b=0),这
时函数是正比例函数.2.函数图象的位置.
(1)直线y=kx+b(k,b是常数,k≠0)与直线y=kx(k是常数,k≠0)的位置关系:
①直线y=kx+b(k,b是常数,k≠0)平行于直线y=kx(k是常数,k≠0);
②当b>0时,把直线y=kx向上平移b个单位长度,可得直线y=kx+b;当b<0时,把直线y=kx向下平移|b|个单位长度,可得直线y=kx+b.(2)直线y1=k1x+b1与直线y2=k2x+b2(k1≠0,k2≠0)的位置关
系:
①k1≠k2?y1与y2相交;
② y1与y2相交于y轴上的同一点;
? y1与y2平行;
y1与y2重合.知识点 2 一次函数图象位置与k与b的关系
【例2】关于x的一次函数y=kx+k2+1的图象可能正确的是( )【解题探究】选__.函数y=kx+k2+1的图象与y轴交于点
_________,∵k2+1>0,∴图象与y轴的交点在y轴的_______上.
分析函数图象只有选项__满足题意,故选__.(0,k2+1)正半轴CCC【总结提升】一次函数y=kx+b图象位置的四种情况
(1)k>0,b>0?函数y=kx+b的图象经过第一、二、三象限.
(2)k>0,b<0?函数y=kx+b的图象经过第一、三、四象限.
(3)k<0,b>0?函数y=kx+b的图象经过第一、二、四象限.
(4)k<0,b<0?函数y=kx+b的图象经过第二、三、四象限.题组一:一次函数图象的画法
1.下列各点在正比例函数y=-10x的图象上的是( )
A.(1,10) B.(2,-5)
C.(-1,10) D.(-2,-5)
【解析】选C.当x=1时,y=-10x=-10×1=-10,
当x=2时,y=-20,当x=-1时,y=10,当x=-2时,y=20.2.直线y=kx-1一定经过点( )
A.(1,0) B.(1,k) C.(0,k) D.(0,-1)
【解析】选D.∵直线y=kx-1中b=-1,
∴此直线一定与y轴相交于(0,-1)点,
∴此直线一定过点(0,-1).3.将函数y=-3x+3的图象向上平移2个单位,得到函数的图象是 .
【解析】原直线的k=-3,b=3;向上平移2个单位得到了新直线,那么新直线的k=-3,b=3+2=5.∴新直线的关系式为
y=-3x+5.
答案:y=-3x+54.在正比例函数y=-3mx中,函数y的值随x值的增大而增大,则P(m,5)在第 象限.
【解析】∵正比例函数y=-3mx中,函数y的值随x值的增大而增大,
∴-3m>0,解得m<0,∴点P(m,5)在第二象限.
答案:二5.某学校的复印任务原来由甲复印社承接,其收费y(元)与复印页数x(页)的关系如表:(1)若收费y(元)与复印页数x(页)满足学过的某一函数关系,求函数的关系式.
(2)现在乙复印社表示:若学校先按每月付给200元的承包费,则可按每页0.15元收费.则乙复印社每月收费y(元)与复印页数x(页)的函数关系为 .(3)在给出的坐标系内画出(1)(2)中的函数图象,并回答每月复印页数在1200左右应选择哪个复印社?【解析】(1)根据题意,收费y(元)与复印页数x(页)的关系式为y=0.4x(x≥0).
(2)乙复印社每月收费y(元)由承包费和复印费两部分组成,所以乙复印社每月收费y(元)与复印页数x(页)的函数关系为y=0.15x+200(x≥0).(3)作图:
由图象可知,当每月复印页数在1200左右时,选择乙复印社更合算.题组二:一次函数图象位置与k与b的关系
1.若实数a,b,c满足a+b+c=0,且a
【解析】选C.由题意得:函数的k=-1,b=1,
∴函数为减函数,且与y轴的交点在y轴的正半轴,
结合选项可得C符合题意.3.一次函数y=x-2的图象不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】选B.一次函数y=x-2,
∵k=1>0,∴函数图象经过第一、三象限.
∵b=-2<0,∴函数图象与y轴负半轴相交,经过第三、四象限,
∴函数图象不经过第二象限.4.如图,一次函数
y=(m-2)x-1的图象经过第二、三、四
象限,则m的取值范围是( )
A.m>0 B.m<0
C.m>2 D.m<2
【解析】选D.由图象知一次函数y=(m-2)x-1的图象经过第二、三、四象限得m-2<0,解得m<2.5.若点(m,n)在函数y=2x+1的图象上,则2m-n的值是( )
A.2 B.-2 C.1 D.-1
【解析】选D.把点(m,n)代入函数关系式得n=2m+1,
∴2m-n=-1.6.已知一次函数y=(6+3m)x+n-4.
(1)当m,n为何值时,函数的图象过原点?
(2)当m,n满足什么条件时,函数的图象经过第一、二、三象限?【解析】(1)∵一次函数y=(6+3m)x+n-4的图象过原点,
∴6+3m≠0,且n-4=0,
解得,m≠-2,n=4.
(2)∵该函数的图象经过第一、二、三象限,
∴6+3m>0,且n-4>0,
解得m>-2,n>4.【想一想错在哪?】 已知一次函数y=(k-2)x+k不经过第三 象限,求k的取值范围.
提示:忽略正比例函数是特殊的一次函数的情形.
