18.2.3 正方形同步测试题3(含解析)
文档属性
| 名称 | 18.2.3 正方形同步测试题3(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 13:00:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2019-2020学年八年级下学期
18.2.3正方形
(时间60分钟 总分100分)
一、选择题(每小题5分,共30分)
1.下列说法正确的是( )
A.对角线相等且互相垂直的四边形是菱形
B.对角线互相平分的四边形是正方形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等且互相平分的四边形是矩形
2.如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )
A. B. C. D.
3.如图,正方形ABCD的边长为1,则正方形ACEF的面积为( )
A.2 B.3 C.4 D.5
4.如图,P是边长为1的正方形ABCD的对角线BD上的一点,点是AB的中点,则PA+PE的最小值是( )
A. B. C. D.
5.把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB'C'D',边BC与D'C'交于点0,则四边形ABOD'的周长是( )
A. B.6 C. D.
6..如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )
A. B. C. D.
二、填空题(每小题5分,共20分)
7.如图,四边形ABOC是边长为4的正方形,则A点的坐标是_________
8.E为正方形ABCD外的一点,AE=AD,且∠ADE=75°,∠AEB=________。
9.如图,在正方形ABCD的外侧,作等边ADE,则∠EBD=__________
10.已知正方形ABCD中,点E在边DC上,DE=2,EC=1,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则EF的长为__________.
三、解答题(共5题,共50分)
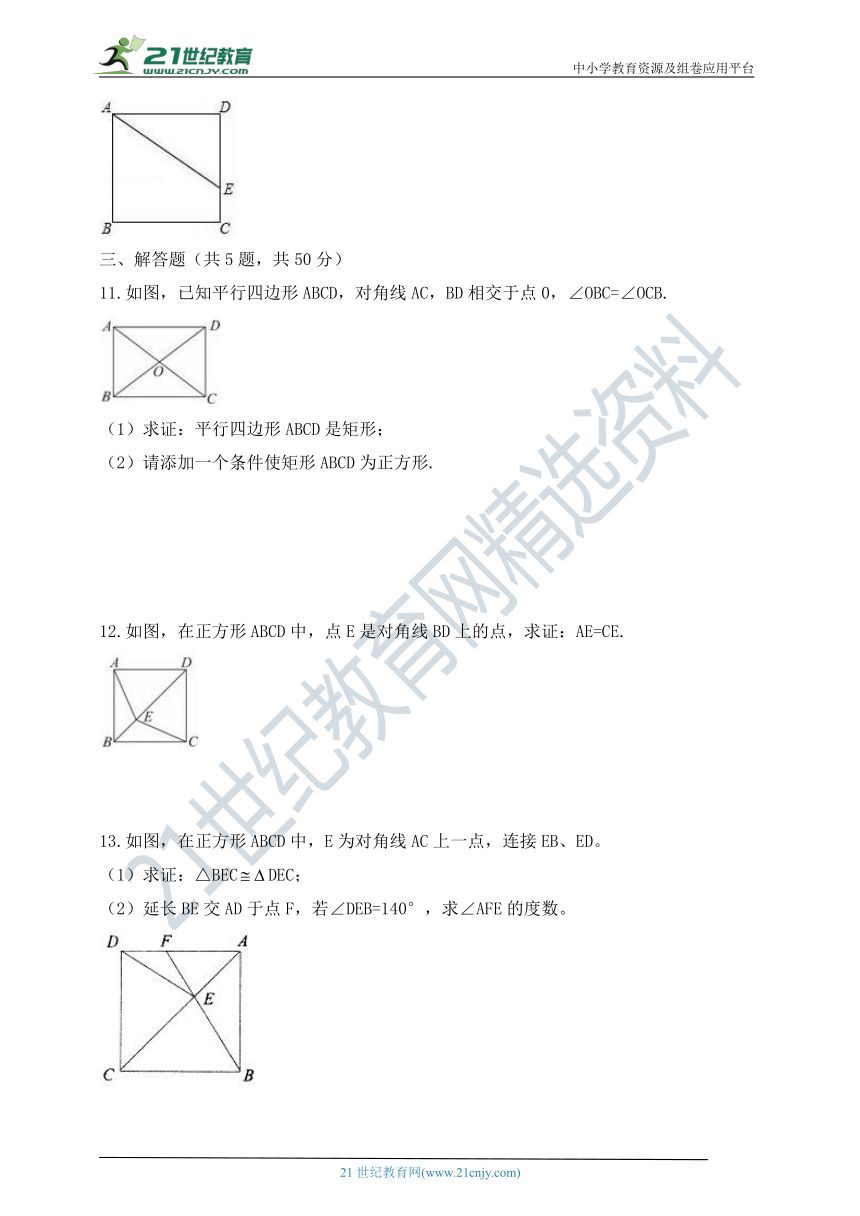
11.如图,已知平行四边形ABCD,对角线AC,BD相交于点0,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.
12.如图,在正方形ABCD中,点E是对角线BD上的点,求证:AE=CE.
13.如图,在正方形ABCD中,E为对角线AC上一点,连接EB、ED。
(1)求证:△BECDEC;
(2)延长BE交AD于点F,若∠DEB=140°,求∠AFE的度数。
14.如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
求证
15.如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BELAP于点E,DFAP于点F.
(1)求证:EF=DF-BE;
(2)若ADF的周长为,求EF的长.
答案
1.【解析】A、菱形的对角线互相垂直目平分,故A错误;B、对角线互相平分的四边形式应该是平行四边形,故B错误;C、对角线互相垂直的四边形并不能断定为平行四边形,故C错误;D、对角线相等且互相平分的四边形是矩形,故D正确.故选D。
2.【解析】正方形对角线平分直角,故∠ACD=45°,已知DCCE,则∠ACE=135°,又:CE=AC,所以∠E=22.5°,故答案为D
3.【解析】由勾股定理得:,乘方得:,故选B.
4.【解析】连接AC,EC,EC与BD交于点P,此时PA+PE的最小,正方形ABCD中,AB=BC=1,E为AB中点,,,故选A.
5.【解析】连接BC',旋转角∠BAB'=45°,∠BAD'=45°,
所以B在对角线AC'上,因为B'C'=AB'=3,在RtAB'C'中,
,在等腰RtOBC'中,
,在直角三角形OBC'中,
所以四边形ABOD'的周长是:
故选A。
6.【解析】延长AE交DF于G,如图:
因为AB=5,AE=3,BE=4,
所以ABE是直角三角形,
所以同理可得DFC是直角三角形,可得AGD是直角三角形,
所以ABE+∠BAE=∠DAE+∠BAE,
所以∠GAD=∠EBA,同理可得:∠ADG=∠BAE,在AGD和BAE中,
同理可得:GF=1
,故选D。
7.【解析】
8.【解析】30度
因为角ADE=75
AB=AD
所以三角形ADE为等腰三角形
角ADE=角AED=75
角EAD就等于30度
在正方形ABCD中角BAD=90
所以角BAE=90+30=120
又因为AD=AB=AE
所以三角形ABE为等腰三角形
角ABE=角AEB=(180-120)/2=30
9.【解析】如图,四边形ABCD是正方形,所以AB=AD,∠BAD=90°,∠ABD=45°,
因为ADE是等边三角形,所以AD=AE=AB,∠DAE=60°,
所以∠BAE=150°,AB=AE,
因为∠ABE=∠AEB=15°,
所以∠EBD=∠ABD-∠ABE=45°-15°=30°
故答案为30°.
10.【解析】在正方形ABCD中,AB=AD,∠ABC=∠D=90°,由旋转的性质得,AF=AE,
在RtABF和RtADE中,,
,,所以正方形的边长为2+1=3,
①点F在线段BC上时,FC=3-2=1,
②点F在CB的延长线上时,FC=3+2=5,
综上所述,EF的长为
11.【解析】(1)因为四边形ABCD是平行四边形,所以0A=OC,OB=OD,因为∠0BC=∠0CB,所以OB=OC,所以AC=BD,所以平行四边形ABCD是矩形
(2)AB=AD(或ACLBD答案不唯一).理由:因为四边形ABCD是矩形,又AB=AD,所以四边形ABCD是正方形(或::四边形ABCD是矩形,又ACBD,四边形ABCD是正方形)
12.【解析】因为四边形ABCD为正方形,AB=CB,∠ABE=∠CBE.在ABE和CBE中,
,
13.【解析】(1)证明:“四边形ABCD是正方形,所以CD=CB.
因为AC是正方形的对角线,所以∠DCA=∠8CA
又CE=CE,
(2)因为∠DEB=140°
由可得∠DEC =∠BEC=1402=70°,
所以∠AEF=∠BEC=70°,又因为AC是正方形的对角线,∠DAB=90°,所以∠DAC=∠BAC=902=45,在△AEF中,∠AFE=180°-70°-45°=65°
14.【解析】(1)四边形ABCD是正方形,所以∠ABC=∠DCB=90°,因为PB=PC,所以∠PBC=∠PCB.所以∠ABC-∠PBC=∠DCB-∠PCB,即∠ABP=∠DCP.又AB=DC,PB=PC,
(2)证明:因为四边形ABCD是正方形,所以∠BAC=∠DAC=45°,,又因为AP=AB=AD,所以DP=AP=AD.
所以APD是等边三角形.
15.【解析】(1)
因为四边形ABCD为正方形,
在ADF和BAE中,
(2)解:设DF=a,AF=b,EF=DF-AF=a-b>0,
因为ADF的周长为
即,由勾股定理得
即
即
_21?????????è?????(www.21cnjy.com)_
人教版2019-2020学年八年级下学期
18.2.3正方形
(时间60分钟 总分100分)
一、选择题(每小题5分,共30分)
1.下列说法正确的是( )
A.对角线相等且互相垂直的四边形是菱形
B.对角线互相平分的四边形是正方形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等且互相平分的四边形是矩形
2.如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )
A. B. C. D.
3.如图,正方形ABCD的边长为1,则正方形ACEF的面积为( )
A.2 B.3 C.4 D.5
4.如图,P是边长为1的正方形ABCD的对角线BD上的一点,点是AB的中点,则PA+PE的最小值是( )
A. B. C. D.
5.把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB'C'D',边BC与D'C'交于点0,则四边形ABOD'的周长是( )
A. B.6 C. D.
6..如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )
A. B. C. D.
二、填空题(每小题5分,共20分)
7.如图,四边形ABOC是边长为4的正方形,则A点的坐标是_________
8.E为正方形ABCD外的一点,AE=AD,且∠ADE=75°,∠AEB=________。
9.如图,在正方形ABCD的外侧,作等边ADE,则∠EBD=__________
10.已知正方形ABCD中,点E在边DC上,DE=2,EC=1,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则EF的长为__________.
三、解答题(共5题,共50分)
11.如图,已知平行四边形ABCD,对角线AC,BD相交于点0,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.
12.如图,在正方形ABCD中,点E是对角线BD上的点,求证:AE=CE.
13.如图,在正方形ABCD中,E为对角线AC上一点,连接EB、ED。
(1)求证:△BECDEC;
(2)延长BE交AD于点F,若∠DEB=140°,求∠AFE的度数。
14.如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
求证
15.如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BELAP于点E,DFAP于点F.
(1)求证:EF=DF-BE;
(2)若ADF的周长为,求EF的长.
答案
1.【解析】A、菱形的对角线互相垂直目平分,故A错误;B、对角线互相平分的四边形式应该是平行四边形,故B错误;C、对角线互相垂直的四边形并不能断定为平行四边形,故C错误;D、对角线相等且互相平分的四边形是矩形,故D正确.故选D。
2.【解析】正方形对角线平分直角,故∠ACD=45°,已知DCCE,则∠ACE=135°,又:CE=AC,所以∠E=22.5°,故答案为D
3.【解析】由勾股定理得:,乘方得:,故选B.
4.【解析】连接AC,EC,EC与BD交于点P,此时PA+PE的最小,正方形ABCD中,AB=BC=1,E为AB中点,,,故选A.
5.【解析】连接BC',旋转角∠BAB'=45°,∠BAD'=45°,
所以B在对角线AC'上,因为B'C'=AB'=3,在RtAB'C'中,
,在等腰RtOBC'中,
,在直角三角形OBC'中,
所以四边形ABOD'的周长是:
故选A。
6.【解析】延长AE交DF于G,如图:
因为AB=5,AE=3,BE=4,
所以ABE是直角三角形,
所以同理可得DFC是直角三角形,可得AGD是直角三角形,
所以ABE+∠BAE=∠DAE+∠BAE,
所以∠GAD=∠EBA,同理可得:∠ADG=∠BAE,在AGD和BAE中,
同理可得:GF=1
,故选D。
7.【解析】
8.【解析】30度
因为角ADE=75
AB=AD
所以三角形ADE为等腰三角形
角ADE=角AED=75
角EAD就等于30度
在正方形ABCD中角BAD=90
所以角BAE=90+30=120
又因为AD=AB=AE
所以三角形ABE为等腰三角形
角ABE=角AEB=(180-120)/2=30
9.【解析】如图,四边形ABCD是正方形,所以AB=AD,∠BAD=90°,∠ABD=45°,
因为ADE是等边三角形,所以AD=AE=AB,∠DAE=60°,
所以∠BAE=150°,AB=AE,
因为∠ABE=∠AEB=15°,
所以∠EBD=∠ABD-∠ABE=45°-15°=30°
故答案为30°.
10.【解析】在正方形ABCD中,AB=AD,∠ABC=∠D=90°,由旋转的性质得,AF=AE,
在RtABF和RtADE中,,
,,所以正方形的边长为2+1=3,
①点F在线段BC上时,FC=3-2=1,
②点F在CB的延长线上时,FC=3+2=5,
综上所述,EF的长为
11.【解析】(1)因为四边形ABCD是平行四边形,所以0A=OC,OB=OD,因为∠0BC=∠0CB,所以OB=OC,所以AC=BD,所以平行四边形ABCD是矩形
(2)AB=AD(或ACLBD答案不唯一).理由:因为四边形ABCD是矩形,又AB=AD,所以四边形ABCD是正方形(或::四边形ABCD是矩形,又ACBD,四边形ABCD是正方形)
12.【解析】因为四边形ABCD为正方形,AB=CB,∠ABE=∠CBE.在ABE和CBE中,
,
13.【解析】(1)证明:“四边形ABCD是正方形,所以CD=CB.
因为AC是正方形的对角线,所以∠DCA=∠8CA
又CE=CE,
(2)因为∠DEB=140°
由可得∠DEC =∠BEC=1402=70°,
所以∠AEF=∠BEC=70°,又因为AC是正方形的对角线,∠DAB=90°,所以∠DAC=∠BAC=902=45,在△AEF中,∠AFE=180°-70°-45°=65°
14.【解析】(1)四边形ABCD是正方形,所以∠ABC=∠DCB=90°,因为PB=PC,所以∠PBC=∠PCB.所以∠ABC-∠PBC=∠DCB-∠PCB,即∠ABP=∠DCP.又AB=DC,PB=PC,
(2)证明:因为四边形ABCD是正方形,所以∠BAC=∠DAC=45°,,又因为AP=AB=AD,所以DP=AP=AD.
所以APD是等边三角形.
15.【解析】(1)
因为四边形ABCD为正方形,
在ADF和BAE中,
(2)解:设DF=a,AF=b,EF=DF-AF=a-b>0,
因为ADF的周长为
即,由勾股定理得
即
即
_21?????????è?????(www.21cnjy.com)_
