28.1锐角三角函数(第二课时)余弦和正切 课件(共25张PPT)
文档属性
| 名称 | 28.1锐角三角函数(第二课时)余弦和正切 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 16:36:33 | ||
图片预览





文档简介
(共24张PPT)
课前准备
1.内容:《28.1锐角三角函数(第二课时) 余弦与正切》,大家提前预习一下相关内容
2.请大家准备好练习本和笔,做好练习和记录
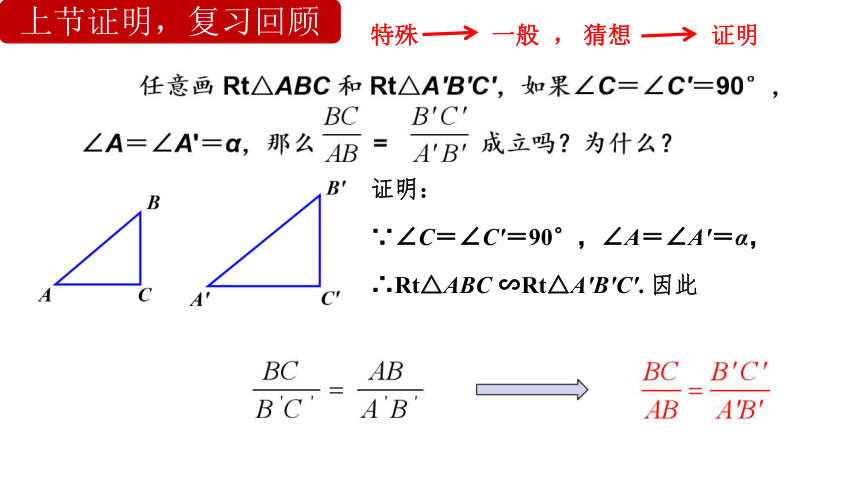
复习:如右图所示
∠A的对边为BC
∠A的邻边为AC
∠A的斜边为AB
请大家自己说出∠B的对边、
邻边和斜边分别是哪些线段?
28.1锐角三角函数(第二课时) 余弦与正切
锐角三角函数家族
正弦
余弦
正切
余切
上节证明,复习回顾
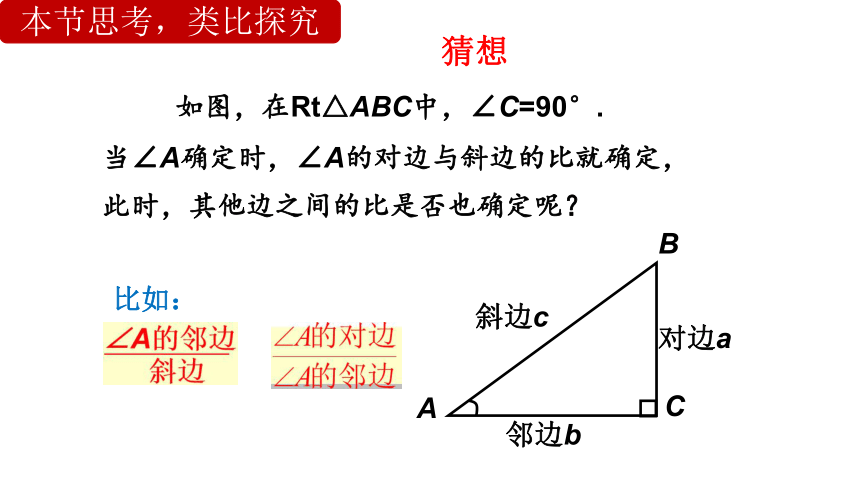
证明:
∵∠C=∠C'=90°,∠A=∠A'=α,
∴Rt△ABC ∽Rt△A'B'C'. 因此
特殊 一般 , 猜想 证明
在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的对边与斜边的比都是一个固定值.
上节证明,复习回顾
∠A的正弦
如图,在Rt△ABC中,∠C=90°.
A
C
B
对边a
邻边b
斜边c
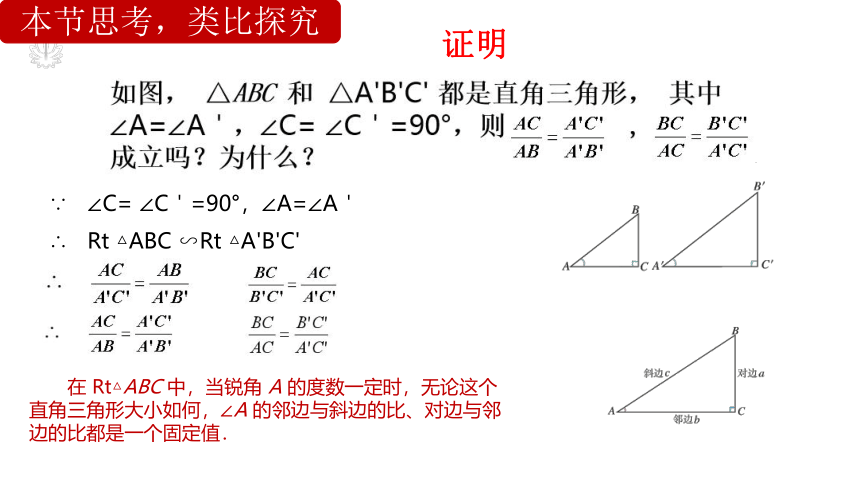
当∠A确定时,∠A的对边与斜边的比就确定,此时,其他边之间的比是否也确定呢?
本节思考,类比探究
比如:
猜想
探究新知
∴ Rt △ABC ∽Rt △A'B'C'
∵ ∠C= ∠C'=90°,∠A=∠A'
在 Rt△ABC 中,当锐角 A 的度数一定时,无论这个直角三角形大小如何,∠A 的邻边与斜边的比、对边与邻边的比都是一个固定值.
本节思考,类比探究
证明
探究新知
我们把∠A 的邻边与斜边的比叫做∠A 的余弦,记作 cos A,即
我们把∠A 的对边与邻边的比叫做∠A 的正切,记作 tan A,即
类比总结,本节概念
在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的邻边与斜边的比、对边与邻边的比都是一个固定值.
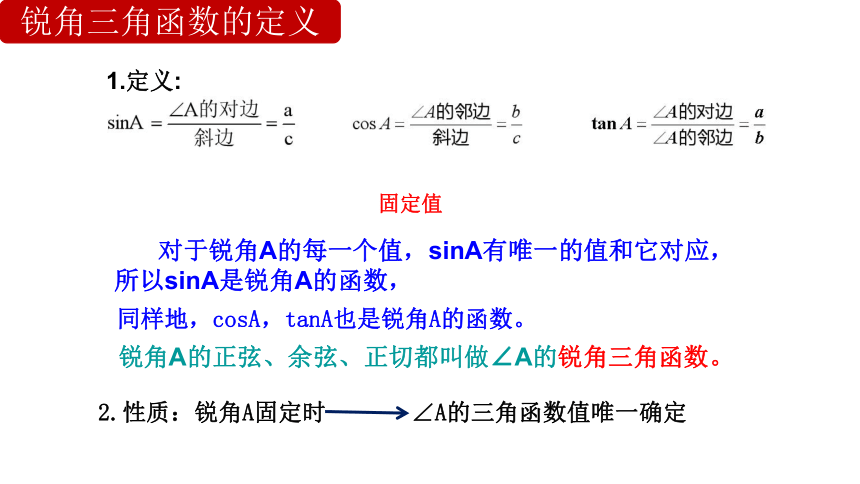
锐角三角函数的定义
固定值
对于锐角A的每一个值,sinA有唯一的值和它对应,所以sinA是锐角A的函数,
同样地,cosA,tanA也是锐角A的函数。
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。
2.性质:锐角A固定时 ∠A的三角函数值唯一确定
1.定义:
在Rt△ABC中,∠C = 90°,AC = 12,AB =13.
sinA=______,cosA=______,tanA=____,
sinB=______,cosB=______,tanB=____.
快速抢答
5
例1 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理得
已知直角三角形两边求锐角三角函数的值
中考素养1
8
方法点拨
已知直角三角形中的两条边求锐角三角函数值的一般思路是:当所涉及的边是已知时,直接利用定义求锐角三角函数值;当所涉及的边未知时,可考虑运用勾股定理的知识求得边的长度,然后根据定义求锐角三角函数值.
中考素养2
在直角三角形中,如果已知一边长及一个锐角的某个三角函数值,即可求出其它的所有锐角三角函数值.
基础练习
B
数形结合
提高练习
提高检测
A
D
设字母
1.(广州中考)如图,旗杆高AB=8m,某一时刻,旗杆影子
长BC=16m,则tanC=______.
A
B
C
链接中考基础题
链接中考基础题
如图,在△ABC中,AB=AC=4,BC=6.
求cosB 及 tanB 的值.
解:过点 A 作 AD⊥BC 于 D.
∵ AB = AC,
∴ BD = CD = 3,
A
B
C
D
提示:求锐角的三角函数值问题,当图形中没有直角三角形时,可用恰当的方法构造直角三角形.
拓展延伸
锐角三角函数应在Rt△中使用,如果没有Rt△,则要通过做辅助线来构造Rt△
如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为___.
贴近中考中档题
转化 构造
课堂小结
1.定义:正弦、余弦、正切的定义及它们为什么是函数
2.性质:锐角A固定时 ∠A的三角函数值唯一确定
3.应用:
①以已知直角三角形两边求锐角三角函数的值
②已知一边及一锐角三角函数值求其他函数值
4.注意:锐角A的三角函数值只与∠A的度数有关,与它是否在Rt△中无关,但如果想使用锐角三角函数得出边与边之间的比值关系,就必须将其放在Rt△环境中,没有就需要做辅助线构造Rt△
1. (贵阳中考)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
B
思维体操
思维体操
B
思维体操
3.如图,△ABC的顶点都是正方形网格中的格点,
则tan∠BAC等于 .
课前准备
1.内容:《28.1锐角三角函数(第二课时) 余弦与正切》,大家提前预习一下相关内容
2.请大家准备好练习本和笔,做好练习和记录
复习:如右图所示
∠A的对边为BC
∠A的邻边为AC
∠A的斜边为AB
请大家自己说出∠B的对边、
邻边和斜边分别是哪些线段?
28.1锐角三角函数(第二课时) 余弦与正切
锐角三角函数家族
正弦
余弦
正切
余切
上节证明,复习回顾
证明:
∵∠C=∠C'=90°,∠A=∠A'=α,
∴Rt△ABC ∽Rt△A'B'C'. 因此
特殊 一般 , 猜想 证明
在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的对边与斜边的比都是一个固定值.
上节证明,复习回顾
∠A的正弦
如图,在Rt△ABC中,∠C=90°.
A
C
B
对边a
邻边b
斜边c
当∠A确定时,∠A的对边与斜边的比就确定,此时,其他边之间的比是否也确定呢?
本节思考,类比探究
比如:
猜想
探究新知
∴ Rt △ABC ∽Rt △A'B'C'
∵ ∠C= ∠C'=90°,∠A=∠A'
在 Rt△ABC 中,当锐角 A 的度数一定时,无论这个直角三角形大小如何,∠A 的邻边与斜边的比、对边与邻边的比都是一个固定值.
本节思考,类比探究
证明
探究新知
我们把∠A 的邻边与斜边的比叫做∠A 的余弦,记作 cos A,即
我们把∠A 的对边与邻边的比叫做∠A 的正切,记作 tan A,即
类比总结,本节概念
在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的邻边与斜边的比、对边与邻边的比都是一个固定值.
锐角三角函数的定义
固定值
对于锐角A的每一个值,sinA有唯一的值和它对应,所以sinA是锐角A的函数,
同样地,cosA,tanA也是锐角A的函数。
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。
2.性质:锐角A固定时 ∠A的三角函数值唯一确定
1.定义:
在Rt△ABC中,∠C = 90°,AC = 12,AB =13.
sinA=______,cosA=______,tanA=____,
sinB=______,cosB=______,tanB=____.
快速抢答
5
例1 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理得
已知直角三角形两边求锐角三角函数的值
中考素养1
8
方法点拨
已知直角三角形中的两条边求锐角三角函数值的一般思路是:当所涉及的边是已知时,直接利用定义求锐角三角函数值;当所涉及的边未知时,可考虑运用勾股定理的知识求得边的长度,然后根据定义求锐角三角函数值.
中考素养2
在直角三角形中,如果已知一边长及一个锐角的某个三角函数值,即可求出其它的所有锐角三角函数值.
基础练习
B
数形结合
提高练习
提高检测
A
D
设字母
1.(广州中考)如图,旗杆高AB=8m,某一时刻,旗杆影子
长BC=16m,则tanC=______.
A
B
C
链接中考基础题
链接中考基础题
如图,在△ABC中,AB=AC=4,BC=6.
求cosB 及 tanB 的值.
解:过点 A 作 AD⊥BC 于 D.
∵ AB = AC,
∴ BD = CD = 3,
A
B
C
D
提示:求锐角的三角函数值问题,当图形中没有直角三角形时,可用恰当的方法构造直角三角形.
拓展延伸
锐角三角函数应在Rt△中使用,如果没有Rt△,则要通过做辅助线来构造Rt△
如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为___.
贴近中考中档题
转化 构造
课堂小结
1.定义:正弦、余弦、正切的定义及它们为什么是函数
2.性质:锐角A固定时 ∠A的三角函数值唯一确定
3.应用:
①以已知直角三角形两边求锐角三角函数的值
②已知一边及一锐角三角函数值求其他函数值
4.注意:锐角A的三角函数值只与∠A的度数有关,与它是否在Rt△中无关,但如果想使用锐角三角函数得出边与边之间的比值关系,就必须将其放在Rt△环境中,没有就需要做辅助线构造Rt△
1. (贵阳中考)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
B
思维体操
思维体操
B
思维体操
3.如图,△ABC的顶点都是正方形网格中的格点,
则tan∠BAC等于 .
