2019-2020学年北京版小学五年级下册期末考试数学试卷2(解析版)
文档属性
| 名称 | 2019-2020学年北京版小学五年级下册期末考试数学试卷2(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 380.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 21:57:45 | ||
图片预览


文档简介
2019-2020学年北京版小学五年级下册期末考试数学试卷
一.选择题(共10小题)
1.最少可以用( )个小正方体就可以摆出一个更大的正方体.
A.2 B.4 C.6 D.8
2.下面分数中,与相等的是( )
A. B. C. D.
3.一个木桶,最多可以装水16L.我们就说,这个木桶的( )是16L.
A.质量 B.表面积 C.容积 D.体积
4.你知道龟兔赛跑的故事吗?乌龟与兔子赛跑,开始兔子跑得快,于是兔子便骄傲起来在途中睡着了,最终乌龟比兔子先到了终点.选一选,下面( )图表示了这个故事
A. B.
C.
5.有45颗糖,平均分成若干份,每份不得少于5颗,也不能多于20颗.一共有( )种分法.
A.5种 B.4种 C.3种 D.2种
6.一张长方形的纸对折两次后的形状(如图),它是原来纸的( )
A.4倍 B. C.
7.根据3×4=12、33×34=1122、333×334=111222,推测3333×3334=( )
A.11111222 B.11122222 C.11112222 D.11111112
8.根据规律,接下来应该是图形( )
A. B. C. D.
9.a、b都是非0自然数,a是b的倍数,a、b的公因数中一定有( )
A.1和b B.1和a C.a和b
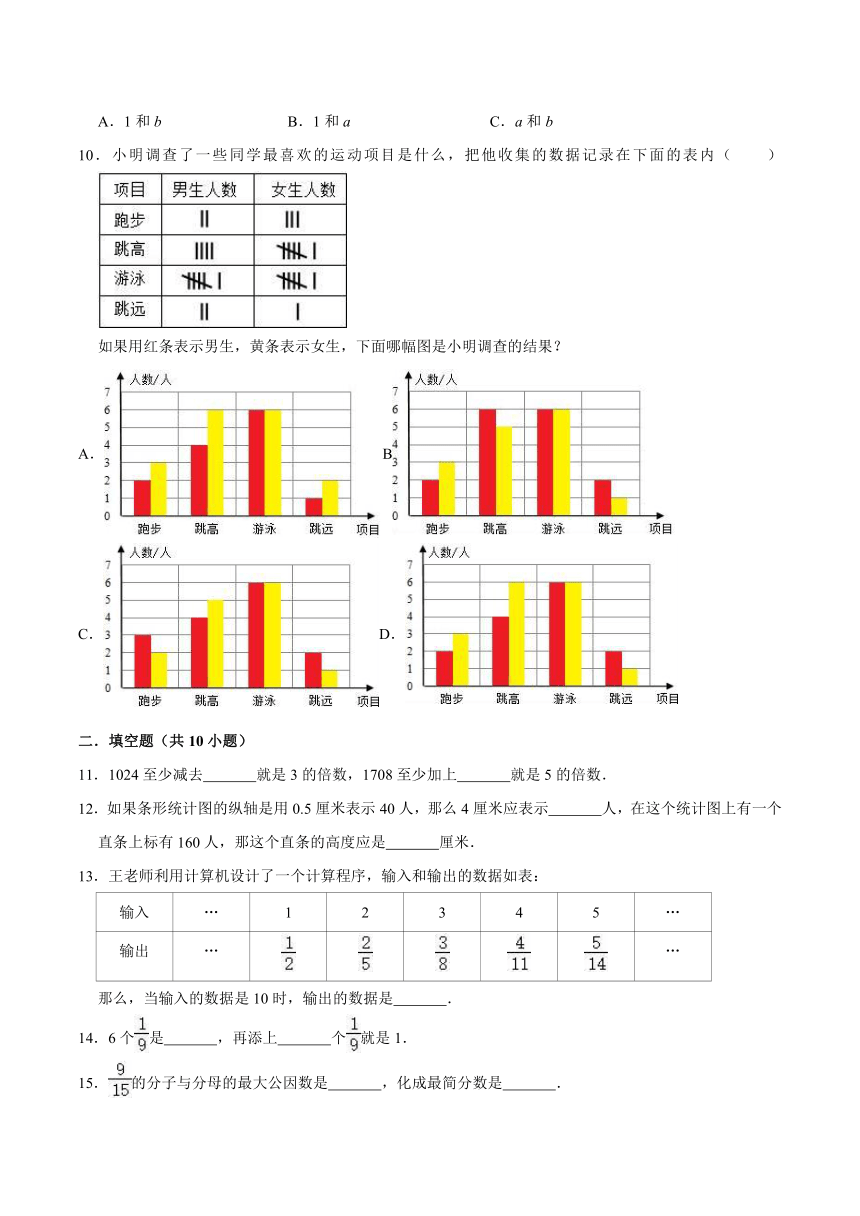
10.小明调查了一些同学最喜欢的运动项目是什么,把他收集的数据记录在下面的表内( )
如果用红条表示男生,黄条表示女生,下面哪幅图是小明调查的结果?
A.B
C.D.
二.填空题(共10小题)
11.1024至少减去 就是3的倍数,1708至少加上 就是5的倍数.
12.如果条形统计图的纵轴是用0.5厘米表示40人,那么4厘米应表示 人,在这个统计图上有一个直条上标有160人,那这个直条的高度应是 厘米.
13.王老师利用计算机设计了一个计算程序,输入和输出的数据如表:
输入 … 1 2 3 4 5 …
输出 … …
那么,当输入的数据是10时,输出的数据是 .
14.6个是 ,再添上 个就是1.
15.的分子与分母的最大公因数是 ,化成最简分数是 .
16.化为带分数是 .
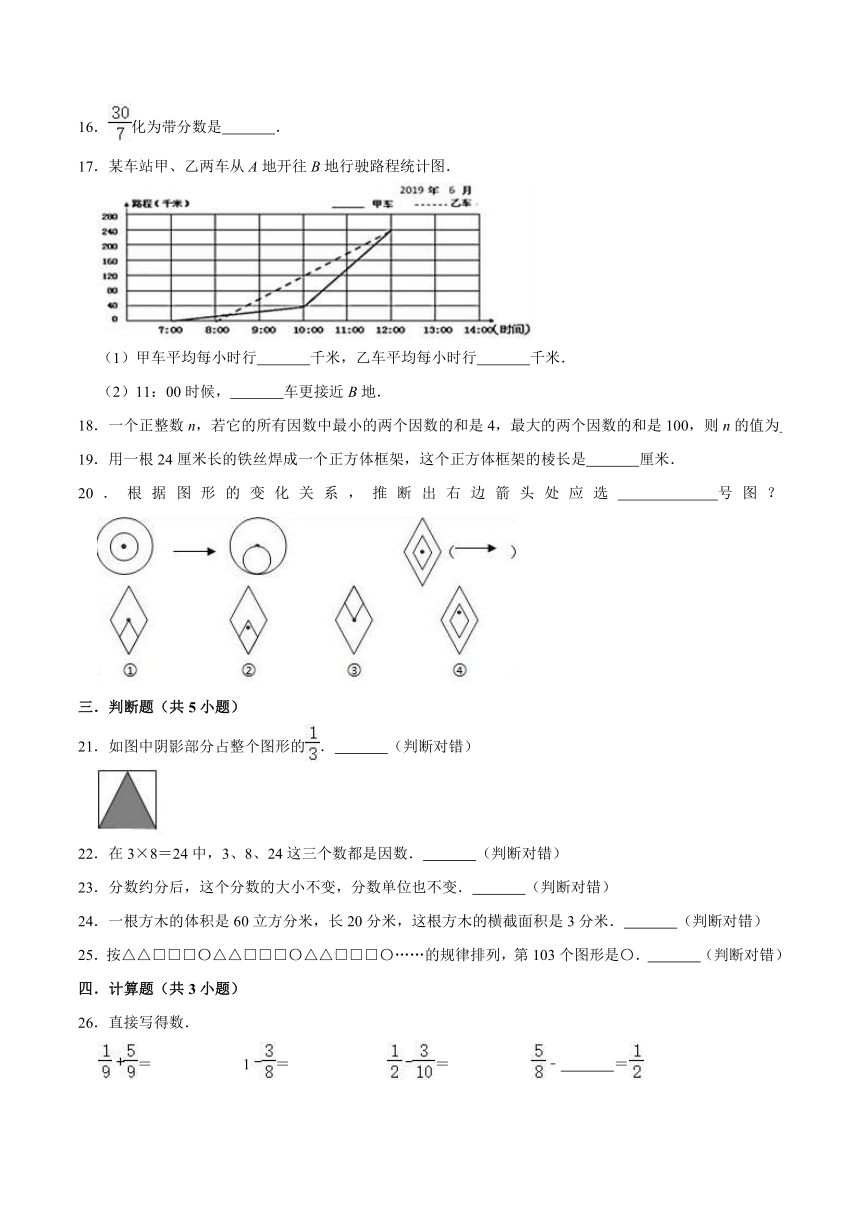
17.某车站甲、乙两车从A地开往B地行驶路程统计图.
(1)甲车平均每小时行 千米,乙车平均每小时行 千米.
(2)11:00时候, 车更接近B地.
18.一个正整数n,若它的所有因数中最小的两个因数的和是4,最大的两个因数的和是100,则n的值为
19.用一根24厘米长的铁丝焊成一个正方体框架,这个正方体框架的棱长是 厘米.
20.根据图形的变化关系,推断出右边箭头处应选 号图?
三.判断题(共5小题)
21.如图中阴影部分占整个图形的. (判断对错)
22.在3×8=24中,3、8、24这三个数都是因数. (判断对错)
23.分数约分后,这个分数的大小不变,分数单位也不变. (判断对错)
24.一根方木的体积是60立方分米,长20分米,这根方木的横截面积是3分米. (判断对错)
25.按△△□□□〇△△□□□〇△△□□□〇……的规律排列,第103个图形是〇. (判断对错)
四.计算题(共3小题)
26.直接写得数.
= 1= = ﹣ =
= = = 1=
27.求下面各组数的最大公因数和最小公倍数.
24和36
20和15
9和27
5和8
28.计算下面长方体的表面积和正方体的体积.(单位:厘米)
五.应用题(共5小题)
29.一根丝绳,第一次用去了它的,第二次用去了它的,两次共用去了它的几分之几?还剩几分之几?
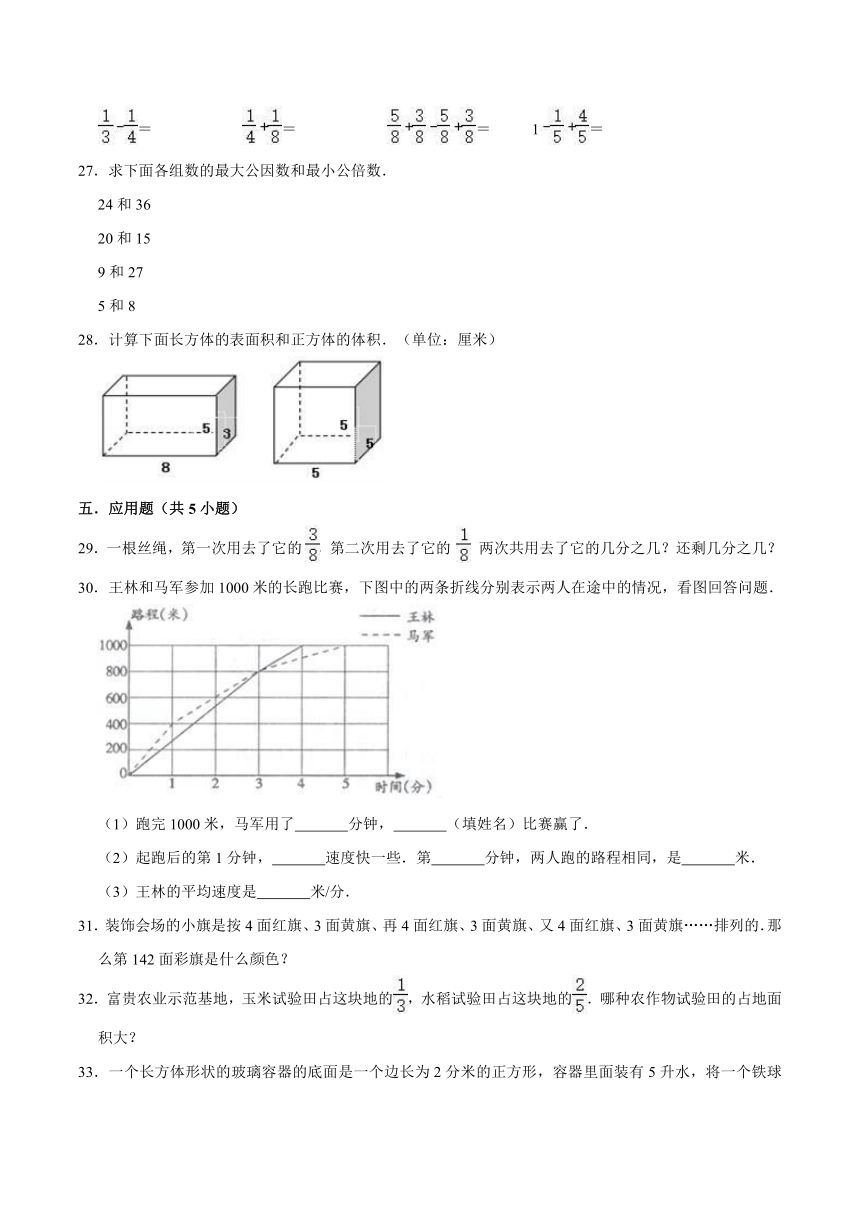
30.王林和马军参加1000米的长跑比赛,下图中的两条折线分别表示两人在途中的情况,看图回答问题.
(1)跑完1000米,马军用了 分钟, (填姓名)比赛赢了.
(2)起跑后的第1分钟, 速度快一些.第 分钟,两人跑的路程相同,是 米.
(3)王林的平均速度是 米/分.
31.装饰会场的小旗是按4面红旗、3面黄旗、再4面红旗、3面黄旗、又4面红旗、3面黄旗……排列的.那么第142面彩旗是什么颜色?
32.富贵农业示范基地,玉米试验田占这块地的,水稻试验田占这块地的.哪种农作物试验田的占地面积大?
33.一个长方体形状的玻璃容器的底面是一个边长为2分米的正方形,容器里面装有5升水,将一个铁球浸没在水中(水未溢出),这时水深1.5分米.这个铁球的体积是多少立方分米?
参考答案与试题解析
一.选择题(共10小题)
1.【分析】根据正方体的体积公式:v=a3,1的立方是1,2的立方是8,3的立方是27,…;据此解答.
【解答】解:因为1的立方是1,2的立方是8,3的立方是27,…;
所以最少可以用8个小正方体就可以拼成一个更大的正方体.
故选:D.
【点评】此题考查的目的是理解掌握正方体的体积公式.
2.【分析】可以根据分数的基本性质把这个分数的分子和分母同时扩大或缩小相同的倍数(0除外),然后找出与这个分数相等的分数.
【解答】解:A、=,>;
B、=,>;
C、=,<;
D、=;
故选:D.
【点评】此题考查学生对分数基本性质的掌握情况.
3.【分析】根据容积的含义:容器所能容纳物体的体积,叫做它的容积;可知:一个木桶,最多可以装水16L.我们就说这个木桶的容积是16L,即水桶的容积;据此选择即可.
【解答】解:一个木桶,最多可以装水16L.我们就说这个木桶的容积是16L;
故选:C.
【点评】本题主要考查容积的定义,容积是指容器所容纳的物体的体积.
4.【分析】根据复式折线统计图的特点,利用排除法做题.C图的乌龟和兔子一直在跑,中途没有休息,不符合题意;B图虽然兔子中途休息,但依然比乌龟先到达终点,不符合题意;所以应该选B.
【解答】解:选项C图中的乌龟和兔子一直在跑,中途没有休息,不符合题意;
选项A图中虽然兔子中途休息,但依然比乌龟先到达终点,不符合题意;
所以应该选B.
故选:B.
【点评】本题主要考查复式折线统计图的应用,关键根据龟兔赛跑的故事做题.
5.【分析】找到45的约数中>5且<20的有:6,8,9,12,18,依此即可求解.
【解答】解:因为45的约数有:1,3,5,9,15,45,
又因为每份不得少于5颗,也不能多于20颗,
只有5、9,15三种分法;
故选:C.
【点评】考查了一个数的约数的求法,本题要注意找在5和20之间的约数.
6.【分析】根据题意,一张长方形的纸对折一次,是原来纸的,两次后是×=,据此解答即可.
【解答】解:一张长方形的纸对折两次后的形状(如图),它是原来纸的×=;
故选:C.
【点评】解答此题的关键是明确一张长方形的纸每对折一次,得到纸的面积就是上一次的.
7.【分析】根据观察知:当因数是3和4时,它们的积是12,当因数是33,34时,积是1122,当因数是333,334时积是111222,它们的规律是当在每个因数的前面添上一个3时,它的积的前面就是添一个1,后面就要添一个2.也就是因数有3的个数与积中1的个数和2的个数相同.据此解答.
【解答】解:根据观察知:因数有3的个数与积中1的个数和2的个数相同.
3333×3334=11112222.
故选:C.
【点评】本题的关键是找出题目中的规律再进行解答.
8.【分析】观察图形可知,从第二组图形开始,每一次变化都是把前一组图形逆时针旋转90度,由此即可选择.
【解答】解:根据规律,接下来应该是图形;
故选:C.
【点评】根据题干得出这组图形的排列规律是解决此类问题的关键.
9.【分析】因为a、b都是非0自然数,所以它们都有因数1;又因为a是b的倍数,所以它们都有因数b;所以a、b的公因数中一定有1和b;由此解答即可.
【解答】解:a、b都是非0自然数,a是b的倍数,a、b的公因数中一定有1和b;
故选:A.
【点评】此题考查了因数、公因数和最大公因数,比较简单,注意基础知识的积累.
10.【分析】根据统计表可知,跑步的男生有2人、女生有3人,跳高的男生有4人、女生有6人,游泳的男生有6人、女生有6人,跳远的男生有2人、女生有1人,根据这些数据选择条形统计图即可得到答案.
【解答】解:根据分析可知统计表中的数据与选项D的数据相对应.
故选:D.
【点评】此题主要考查的是如何从统计表中获取信息,然后再根据信息选择条形统计图即可.
二.填空题(共10小题)
11.【分析】(1)各个数位上数字的和是3的倍数,这个数就是3的倍数,1024各个数位上的数字的和是1+0+2+4=7,至少再减去1就是3的倍数,据此解答;
(2)个位上是0或5的数就是5的倍数,1078的个位上是8,至少再加上2,即8+2=10,变成个位上是0,据此解答.
【解答】解:(1)1+0+2+4=7,6是3的倍数,
所以至少应减去:7﹣6=1,
(2)1708个位是8,只有个位数是0或5时,才能被5整除;故至少加上2;
故答案为:1,2.
【点评】本题主要考查3和5的倍数特征的灵活运用能力.
12.【分析】在同一个条形统计图中,用固定的长度表示一定数量,本题中0.5厘米表示40人,看4厘米中有多少个这样的单位,然后乘以这个单位长底代表的人数就行了,用160人除以每个单位长度代表的人数,看有多少个单位长度,然后乘以这个单位长度的厘米数就行了.
【解答】解:由题意知,4÷0.5×40=320(人),
160÷40×0.5=2(厘米),
故答案为:320,2.
【点评】此题考查统计图纵轴的长度和单位长度代表的量之间的关系.
13.【分析】观察表格发现,输入的数字是几,输出数的分子就是几;输入1,输出数的分母是1×3﹣1=2,输入2输出数的分母是2×3﹣1=5,输入3输出数的分母是3×3﹣1=8,输入4输出数的分母是4×3﹣1=11,输入5输出数的分母是5×3﹣1=14,输入几,输出数的分母就是这个数的3倍减去1,由此求解.
【解答】解:输入10,输出数的分子就是10;
分母是:10×3﹣1
=30﹣1
=29
所以,输出的数就是.
故答案为:.
【点评】解决本题关键是找出输入数据与输出的数据之间的关系,再由此进行求解.
14.【分析】把单位“1”平均分成9份,每份是,6个就是,即;“1”里面有9个,再添上9﹣6=3个即可.
【解答】解:6个是,即;再添上3个就是1.
故答案为:,3.
【点评】此题是考查分数的意义.把单位“1”平均分成若干份,用分数表示,分母是分成的份数,分子是要表示的份数.
15.【分析】9与15的最大公因数是3,把的分子、分母都除以3即可化成最简分数.
【解答】解:9与15的最大公因数是3
=
答:的分子与分母的最大公因数是 3,化成最简分数是.
故答案为:3,.
【点评】本题主要是考查最简分数的意义及化法.分子、分母只有公因数1的分数就是最简分数;化简分数时,根据分数的基本性质,分子、分母都除以它们的最大公因数.
16.【分析】假分数化带分数时,用分子除以分母,商为带分数的整数部分,余数作分数部分的分子、分母不变.
【解答】解:30÷7=4……2
化为带分数是4.
故答案为:4.
【点评】此题是考查假分数化带分数,属于基础知识,要掌握.
17.【分析】(1)甲车5小时行驶了240千米,用“路程÷时间﹣速度”即可求出它的速度;乙车4小时行驶了240千米,用“路程÷时间﹣速度”即可求出它的速度;
(2)观察统计图可以发现:11:00时候,乙车更接近B地.
【解答】解:(1)240÷5=48(千米)
240÷4=60(千米)
答:甲车平均每小时行 48千米,乙车平均每小时行 60千米.
(2)观察统计图可以发现:11:00时候,乙车更接近B地.
故答案为:48,60;乙.
【点评】此题主要考查的是如何观察复式折线统计图并且从统计图中获取信息,然后再进行计算、解答即可.
18.【分析】最小的两个约数中一定有一个是1,因此另一个是3,说明最大的约数是第二大的约数的3倍,而最大的两个约数之和为100,100÷(3+1)=25,所以最大的两个约数是25和75,这个正整数就是75.
【解答】解:最小的两个约数中一定有一个是1,因此另一个是3,最大的两个约数是:
100÷(3+1)=25
100﹣25=75
所以最大的两个约数是25和75,
这个正整数就是75.
答:这个正整数是75;
故答案为:75.
【点评】此题解答的关键是先求出最小的两个约数,根据最大的约数是第二大的约数的3倍,求出最大的两个约数,进而得出这个正整数.
19.【分析】根据正方体的特征,12条棱的长度都相等,用棱长总和除以12即可.
【解答】解:24÷12=2(厘米),
答:这个正方体框架的棱长是2厘米.
故答案为:2.
【点评】此题考查的目的是理解掌握正方体的特征,以及棱长总和公式的灵活运用.
20.【分析】根据给出的图形可知:小圆到了大圆的内下方,两个圆内切,而且黑点在小圆上;由此变化进行求解.
【解答】解:
小菱形应到大菱形的内下方,它们下边的顶点重合,两条边也重合;小黑点应在菱形的顶点上;应变成:
故选:①.
【点评】对于这类型的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
三.判断题(共5小题)
21.【分析】由题可知,正方形内最大的三角形与正方形等底等高,则三角形的面积是正方形面积的一半,即阴影部分占整个图形的.
【解答】解:正方形内最大的三角形与正方形等底等高,则三角形的面积是正方形面积的一半,即阴影部分占整个图形的;
所以原题说法错误;
故答案为:×.
【点评】解答此题关键是得到正方形内最大的三角形与正方形等底等高,则三角形的面积是正方形面积的一半.
22.【分析】因数和倍数是相对的,是相互依存的,只能说一个数是另一个数的倍数或另一个数是这个数的因数,不能单独存在;由此判断即可.
【解答】解:因为3×8=24,则:24÷3=8,24是3的倍数,3是24的因数,因数和倍数是相对的,
是相互依存的,不能单独存在;
所以原题说法错误.
故答案为:×.
【点评】此题考查了因数和倍数的意义,应明确倍数和因数是相对的,一个不能独立存在.
23.【分析】约分是把分子、分母同时除以一个不为0的数;化成最简分数后,虽然分数大小没变,但是分子和分母都变小了,分数单位只和分母的大小有关,分母是几,分数单位就是几分之一,分母小了,该分数单位就大了.
【解答】解:分数约分后,分子和分母都变小了,而分数单位只和分母有关,分母是几,分数单位就是几分之一,分母小了,而分数单位就大;
所以,原题说法错误.
故答案为:×.
【点评】本题考查分数的约分及其分数单位,认真把握这两个概念是关键.
24.【分析】根据长方体的体积公式:V=Sh,用方木的体积除以长即可求出这根方木的横截面积.
【解答】解:60÷20=3(平方分米)
答:这根方木的横截面积是3平方分米.
故题干的说法是错误的.
故答案为:×.
【点评】此题主要考查长方体的体积公式在实际生活中的应用.
25.【分析】观察图形可知,这组图形是6个图形一个循环,分别按照△△□□□〇的顺序依次排列,所以求出第?103个图形是第几个循环的第几个图形即可解答问题.
【解答】解:103÷6=17(个循环)…1个
所以第103个图形是第18循环的第一个图形,与第一个循环的第一个图形相同,是△.
所以原题”第103个图形是〇“说法错误.
故答案为:×.
【点评】本题考查图形排列的规律:认真找出哪些图形是一组是关键.
四.计算题(共3小题)
26.【分析】根据分数加减法的计算方法进行计算.
﹣( )=,求未知减数,用被减数减去差;
根据加法交换律和结合律进行简算.
【解答】解:
= 1= = ﹣=
= = = 1=
故答案为:.
【点评】口算时,注意运算符号和数据,然后再进一步计算.
27.【分析】对于一般的两个数来说,这两个数的公有质因数的连乘积是这两个数的最大公因数,这两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;当两个数成倍数关系,最大公因数为较小的数,较大的那个数,是这两个数的最小公倍数;是互质数的两个数,它们的最大公因数是1,最小公倍数即这两个数的乘积.
【解答】解:24=2×2×2×3
36=2×2×3×3
最大公约数是2×2×3=12,最小公倍数是2×2×2×3×3=72.
20=2×2×5,
15=3×5,
最大公因数是5,最小公倍数是2×2×3×5=60;
9和27是倍数关系,最大公约数是9,最小公倍数是27;
5和8是互质数,所以它们的最大公因数是1,最小公倍数是这两个数的乘积,5×8=40.
【点评】此题主要考查了求两个数的最大公因数和最小公倍数的方法:对于一般的两个数来说,这两个数的公有质因数的连乘积是这两个数的最大公因数,这两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;当两个数成倍数关系,最大公因数为较小的数,较大的那个数,是这两个数的最小公倍数;是互质数的两个数,它们的最大公因数是1,最小公倍数即这两个数的乘积.
28.【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,正方体的体积=棱长×棱长×棱长,由此代入数据即可解答.
【解答】解:长方体的表面积是:
(8×3+8×5+3×5)×2
=(24+40+15)×2
=79×2
=158(平方厘米)
正方体的体积是:5×5×5=125(立方厘米)
答:长方体的表面积是158平方厘米;正方体的体积是125立方厘米.
【点评】此题考查了长方体和正方体的表面积与体积公式的计算应用.
五.应用题(共5小题)
29.【分析】把两次用去的占得分率相加,就是两次一共用去了几分之几;把这条绳子看作单位“1”,用单位“1”减去两次用去占的分率和,就是还剩下的几分之几.
【解答】解: +=;
1﹣=.
答:两次共用去了它的,还剩.
【点评】此题考查分数加减法应用题以及同分数分数加减法的计算方法,要注意结果化成最简分数.
30.【分析】(1)根据折线统计图可知,跑完1000米,马军用了5分钟,王林用了4分钟,所以王林比赛赢了.;
(2)在起跑后的第1分钟,马军跑了400米,王林大约跑了280米,所以在起跑后的第1分,马军跑的速度快些;在起跑后的第3分钟,两人的折线相重合,此时两人跑的路程同样多,大约是800米;
(3)根据公式路程÷时间=速度进行计算即可得到答案.
【解答】解:(1)跑完1000米,马军用了5分钟,王林比赛赢了.
(2)起跑后的第1分钟,马军速度快一些.第3分钟,两人跑的路程相同,是800米.
(3)1000÷4=250(米)
答:王林的平均速度是米/分.
故答案为:5,王林,马军,3,800,250.
【点评】此题主要考查的是如何从折线统计图中获取信息,然后再根据信息进行分析、计算即可.
31.【分析】按4面红旗、3面黄旗依次不断的出现,是把4+3=7面红旗看成一个循环,用142除以7求出商和余数,再根据余数进行推算.
【解答】解:142÷(4+3)
=142÷7
=20……2
余数是2,所以第142面旗子是第21个循环的第2面,是红色的.
答:第142面彩旗是红色的.
【点评】解决这类问题关键是把重复出现的部分看成一组,根据除法的意义,求出总数量里面有多少个这样的一组,还余几,然后根据余数进行推算.
32.【分析】根据题意,玉米试验田占这块地的,水稻试验田占这块地的;说明和的单位“1”相同,比较这两个分数,分数大的占地面积大,由此判断即可.
【解答】解:=
=
所以<
答:水稻试验田的占地面积大.
【点评】解决本题先找清楚单位“1”是否相同,明确能否直接比较,再根据分数比较大小的方法求解.
33.【分析】首先要明确:升高的那部分水的体积就等于铁球的体积,因此需要先求出升高的水的高度,由原来有水5升,利用长方体的体积公式V=abh即可求出原来的水的高度,用现在的水的高度减去原来的水的高度,就是升高的水的高度,进而可以求出升高的那部分水的体积,问题即可得解.
【解答】解:5升=5立方分米
原来的水的高度:5÷(2×2)
=5÷4
=1.25(分米)
升高的水的高度:1.5﹣1.25=0.25(分米)
铁球的体积:2×2×0.25
=4×0.25
=1(立方分米)
答:这个铁球的体积是1立方分米.
【点评】此题主要考查长方体的体积的计算方法的实际应用,关键是明白:升高的那部分水的体积就等于铁球的体积,求出升高的水的高度,是解答本题的关键.
一.选择题(共10小题)
1.最少可以用( )个小正方体就可以摆出一个更大的正方体.
A.2 B.4 C.6 D.8
2.下面分数中,与相等的是( )
A. B. C. D.
3.一个木桶,最多可以装水16L.我们就说,这个木桶的( )是16L.
A.质量 B.表面积 C.容积 D.体积
4.你知道龟兔赛跑的故事吗?乌龟与兔子赛跑,开始兔子跑得快,于是兔子便骄傲起来在途中睡着了,最终乌龟比兔子先到了终点.选一选,下面( )图表示了这个故事
A. B.
C.
5.有45颗糖,平均分成若干份,每份不得少于5颗,也不能多于20颗.一共有( )种分法.
A.5种 B.4种 C.3种 D.2种
6.一张长方形的纸对折两次后的形状(如图),它是原来纸的( )
A.4倍 B. C.
7.根据3×4=12、33×34=1122、333×334=111222,推测3333×3334=( )
A.11111222 B.11122222 C.11112222 D.11111112
8.根据规律,接下来应该是图形( )
A. B. C. D.
9.a、b都是非0自然数,a是b的倍数,a、b的公因数中一定有( )
A.1和b B.1和a C.a和b
10.小明调查了一些同学最喜欢的运动项目是什么,把他收集的数据记录在下面的表内( )
如果用红条表示男生,黄条表示女生,下面哪幅图是小明调查的结果?
A.B
C.D.
二.填空题(共10小题)
11.1024至少减去 就是3的倍数,1708至少加上 就是5的倍数.
12.如果条形统计图的纵轴是用0.5厘米表示40人,那么4厘米应表示 人,在这个统计图上有一个直条上标有160人,那这个直条的高度应是 厘米.
13.王老师利用计算机设计了一个计算程序,输入和输出的数据如表:
输入 … 1 2 3 4 5 …
输出 … …
那么,当输入的数据是10时,输出的数据是 .
14.6个是 ,再添上 个就是1.
15.的分子与分母的最大公因数是 ,化成最简分数是 .
16.化为带分数是 .
17.某车站甲、乙两车从A地开往B地行驶路程统计图.
(1)甲车平均每小时行 千米,乙车平均每小时行 千米.
(2)11:00时候, 车更接近B地.
18.一个正整数n,若它的所有因数中最小的两个因数的和是4,最大的两个因数的和是100,则n的值为
19.用一根24厘米长的铁丝焊成一个正方体框架,这个正方体框架的棱长是 厘米.
20.根据图形的变化关系,推断出右边箭头处应选 号图?
三.判断题(共5小题)
21.如图中阴影部分占整个图形的. (判断对错)
22.在3×8=24中,3、8、24这三个数都是因数. (判断对错)
23.分数约分后,这个分数的大小不变,分数单位也不变. (判断对错)
24.一根方木的体积是60立方分米,长20分米,这根方木的横截面积是3分米. (判断对错)
25.按△△□□□〇△△□□□〇△△□□□〇……的规律排列,第103个图形是〇. (判断对错)
四.计算题(共3小题)
26.直接写得数.
= 1= = ﹣ =
= = = 1=
27.求下面各组数的最大公因数和最小公倍数.
24和36
20和15
9和27
5和8
28.计算下面长方体的表面积和正方体的体积.(单位:厘米)
五.应用题(共5小题)
29.一根丝绳,第一次用去了它的,第二次用去了它的,两次共用去了它的几分之几?还剩几分之几?
30.王林和马军参加1000米的长跑比赛,下图中的两条折线分别表示两人在途中的情况,看图回答问题.
(1)跑完1000米,马军用了 分钟, (填姓名)比赛赢了.
(2)起跑后的第1分钟, 速度快一些.第 分钟,两人跑的路程相同,是 米.
(3)王林的平均速度是 米/分.
31.装饰会场的小旗是按4面红旗、3面黄旗、再4面红旗、3面黄旗、又4面红旗、3面黄旗……排列的.那么第142面彩旗是什么颜色?
32.富贵农业示范基地,玉米试验田占这块地的,水稻试验田占这块地的.哪种农作物试验田的占地面积大?
33.一个长方体形状的玻璃容器的底面是一个边长为2分米的正方形,容器里面装有5升水,将一个铁球浸没在水中(水未溢出),这时水深1.5分米.这个铁球的体积是多少立方分米?
参考答案与试题解析
一.选择题(共10小题)
1.【分析】根据正方体的体积公式:v=a3,1的立方是1,2的立方是8,3的立方是27,…;据此解答.
【解答】解:因为1的立方是1,2的立方是8,3的立方是27,…;
所以最少可以用8个小正方体就可以拼成一个更大的正方体.
故选:D.
【点评】此题考查的目的是理解掌握正方体的体积公式.
2.【分析】可以根据分数的基本性质把这个分数的分子和分母同时扩大或缩小相同的倍数(0除外),然后找出与这个分数相等的分数.
【解答】解:A、=,>;
B、=,>;
C、=,<;
D、=;
故选:D.
【点评】此题考查学生对分数基本性质的掌握情况.
3.【分析】根据容积的含义:容器所能容纳物体的体积,叫做它的容积;可知:一个木桶,最多可以装水16L.我们就说这个木桶的容积是16L,即水桶的容积;据此选择即可.
【解答】解:一个木桶,最多可以装水16L.我们就说这个木桶的容积是16L;
故选:C.
【点评】本题主要考查容积的定义,容积是指容器所容纳的物体的体积.
4.【分析】根据复式折线统计图的特点,利用排除法做题.C图的乌龟和兔子一直在跑,中途没有休息,不符合题意;B图虽然兔子中途休息,但依然比乌龟先到达终点,不符合题意;所以应该选B.
【解答】解:选项C图中的乌龟和兔子一直在跑,中途没有休息,不符合题意;
选项A图中虽然兔子中途休息,但依然比乌龟先到达终点,不符合题意;
所以应该选B.
故选:B.
【点评】本题主要考查复式折线统计图的应用,关键根据龟兔赛跑的故事做题.
5.【分析】找到45的约数中>5且<20的有:6,8,9,12,18,依此即可求解.
【解答】解:因为45的约数有:1,3,5,9,15,45,
又因为每份不得少于5颗,也不能多于20颗,
只有5、9,15三种分法;
故选:C.
【点评】考查了一个数的约数的求法,本题要注意找在5和20之间的约数.
6.【分析】根据题意,一张长方形的纸对折一次,是原来纸的,两次后是×=,据此解答即可.
【解答】解:一张长方形的纸对折两次后的形状(如图),它是原来纸的×=;
故选:C.
【点评】解答此题的关键是明确一张长方形的纸每对折一次,得到纸的面积就是上一次的.
7.【分析】根据观察知:当因数是3和4时,它们的积是12,当因数是33,34时,积是1122,当因数是333,334时积是111222,它们的规律是当在每个因数的前面添上一个3时,它的积的前面就是添一个1,后面就要添一个2.也就是因数有3的个数与积中1的个数和2的个数相同.据此解答.
【解答】解:根据观察知:因数有3的个数与积中1的个数和2的个数相同.
3333×3334=11112222.
故选:C.
【点评】本题的关键是找出题目中的规律再进行解答.
8.【分析】观察图形可知,从第二组图形开始,每一次变化都是把前一组图形逆时针旋转90度,由此即可选择.
【解答】解:根据规律,接下来应该是图形;
故选:C.
【点评】根据题干得出这组图形的排列规律是解决此类问题的关键.
9.【分析】因为a、b都是非0自然数,所以它们都有因数1;又因为a是b的倍数,所以它们都有因数b;所以a、b的公因数中一定有1和b;由此解答即可.
【解答】解:a、b都是非0自然数,a是b的倍数,a、b的公因数中一定有1和b;
故选:A.
【点评】此题考查了因数、公因数和最大公因数,比较简单,注意基础知识的积累.
10.【分析】根据统计表可知,跑步的男生有2人、女生有3人,跳高的男生有4人、女生有6人,游泳的男生有6人、女生有6人,跳远的男生有2人、女生有1人,根据这些数据选择条形统计图即可得到答案.
【解答】解:根据分析可知统计表中的数据与选项D的数据相对应.
故选:D.
【点评】此题主要考查的是如何从统计表中获取信息,然后再根据信息选择条形统计图即可.
二.填空题(共10小题)
11.【分析】(1)各个数位上数字的和是3的倍数,这个数就是3的倍数,1024各个数位上的数字的和是1+0+2+4=7,至少再减去1就是3的倍数,据此解答;
(2)个位上是0或5的数就是5的倍数,1078的个位上是8,至少再加上2,即8+2=10,变成个位上是0,据此解答.
【解答】解:(1)1+0+2+4=7,6是3的倍数,
所以至少应减去:7﹣6=1,
(2)1708个位是8,只有个位数是0或5时,才能被5整除;故至少加上2;
故答案为:1,2.
【点评】本题主要考查3和5的倍数特征的灵活运用能力.
12.【分析】在同一个条形统计图中,用固定的长度表示一定数量,本题中0.5厘米表示40人,看4厘米中有多少个这样的单位,然后乘以这个单位长底代表的人数就行了,用160人除以每个单位长度代表的人数,看有多少个单位长度,然后乘以这个单位长度的厘米数就行了.
【解答】解:由题意知,4÷0.5×40=320(人),
160÷40×0.5=2(厘米),
故答案为:320,2.
【点评】此题考查统计图纵轴的长度和单位长度代表的量之间的关系.
13.【分析】观察表格发现,输入的数字是几,输出数的分子就是几;输入1,输出数的分母是1×3﹣1=2,输入2输出数的分母是2×3﹣1=5,输入3输出数的分母是3×3﹣1=8,输入4输出数的分母是4×3﹣1=11,输入5输出数的分母是5×3﹣1=14,输入几,输出数的分母就是这个数的3倍减去1,由此求解.
【解答】解:输入10,输出数的分子就是10;
分母是:10×3﹣1
=30﹣1
=29
所以,输出的数就是.
故答案为:.
【点评】解决本题关键是找出输入数据与输出的数据之间的关系,再由此进行求解.
14.【分析】把单位“1”平均分成9份,每份是,6个就是,即;“1”里面有9个,再添上9﹣6=3个即可.
【解答】解:6个是,即;再添上3个就是1.
故答案为:,3.
【点评】此题是考查分数的意义.把单位“1”平均分成若干份,用分数表示,分母是分成的份数,分子是要表示的份数.
15.【分析】9与15的最大公因数是3,把的分子、分母都除以3即可化成最简分数.
【解答】解:9与15的最大公因数是3
=
答:的分子与分母的最大公因数是 3,化成最简分数是.
故答案为:3,.
【点评】本题主要是考查最简分数的意义及化法.分子、分母只有公因数1的分数就是最简分数;化简分数时,根据分数的基本性质,分子、分母都除以它们的最大公因数.
16.【分析】假分数化带分数时,用分子除以分母,商为带分数的整数部分,余数作分数部分的分子、分母不变.
【解答】解:30÷7=4……2
化为带分数是4.
故答案为:4.
【点评】此题是考查假分数化带分数,属于基础知识,要掌握.
17.【分析】(1)甲车5小时行驶了240千米,用“路程÷时间﹣速度”即可求出它的速度;乙车4小时行驶了240千米,用“路程÷时间﹣速度”即可求出它的速度;
(2)观察统计图可以发现:11:00时候,乙车更接近B地.
【解答】解:(1)240÷5=48(千米)
240÷4=60(千米)
答:甲车平均每小时行 48千米,乙车平均每小时行 60千米.
(2)观察统计图可以发现:11:00时候,乙车更接近B地.
故答案为:48,60;乙.
【点评】此题主要考查的是如何观察复式折线统计图并且从统计图中获取信息,然后再进行计算、解答即可.
18.【分析】最小的两个约数中一定有一个是1,因此另一个是3,说明最大的约数是第二大的约数的3倍,而最大的两个约数之和为100,100÷(3+1)=25,所以最大的两个约数是25和75,这个正整数就是75.
【解答】解:最小的两个约数中一定有一个是1,因此另一个是3,最大的两个约数是:
100÷(3+1)=25
100﹣25=75
所以最大的两个约数是25和75,
这个正整数就是75.
答:这个正整数是75;
故答案为:75.
【点评】此题解答的关键是先求出最小的两个约数,根据最大的约数是第二大的约数的3倍,求出最大的两个约数,进而得出这个正整数.
19.【分析】根据正方体的特征,12条棱的长度都相等,用棱长总和除以12即可.
【解答】解:24÷12=2(厘米),
答:这个正方体框架的棱长是2厘米.
故答案为:2.
【点评】此题考查的目的是理解掌握正方体的特征,以及棱长总和公式的灵活运用.
20.【分析】根据给出的图形可知:小圆到了大圆的内下方,两个圆内切,而且黑点在小圆上;由此变化进行求解.
【解答】解:
小菱形应到大菱形的内下方,它们下边的顶点重合,两条边也重合;小黑点应在菱形的顶点上;应变成:
故选:①.
【点评】对于这类型的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
三.判断题(共5小题)
21.【分析】由题可知,正方形内最大的三角形与正方形等底等高,则三角形的面积是正方形面积的一半,即阴影部分占整个图形的.
【解答】解:正方形内最大的三角形与正方形等底等高,则三角形的面积是正方形面积的一半,即阴影部分占整个图形的;
所以原题说法错误;
故答案为:×.
【点评】解答此题关键是得到正方形内最大的三角形与正方形等底等高,则三角形的面积是正方形面积的一半.
22.【分析】因数和倍数是相对的,是相互依存的,只能说一个数是另一个数的倍数或另一个数是这个数的因数,不能单独存在;由此判断即可.
【解答】解:因为3×8=24,则:24÷3=8,24是3的倍数,3是24的因数,因数和倍数是相对的,
是相互依存的,不能单独存在;
所以原题说法错误.
故答案为:×.
【点评】此题考查了因数和倍数的意义,应明确倍数和因数是相对的,一个不能独立存在.
23.【分析】约分是把分子、分母同时除以一个不为0的数;化成最简分数后,虽然分数大小没变,但是分子和分母都变小了,分数单位只和分母的大小有关,分母是几,分数单位就是几分之一,分母小了,该分数单位就大了.
【解答】解:分数约分后,分子和分母都变小了,而分数单位只和分母有关,分母是几,分数单位就是几分之一,分母小了,而分数单位就大;
所以,原题说法错误.
故答案为:×.
【点评】本题考查分数的约分及其分数单位,认真把握这两个概念是关键.
24.【分析】根据长方体的体积公式:V=Sh,用方木的体积除以长即可求出这根方木的横截面积.
【解答】解:60÷20=3(平方分米)
答:这根方木的横截面积是3平方分米.
故题干的说法是错误的.
故答案为:×.
【点评】此题主要考查长方体的体积公式在实际生活中的应用.
25.【分析】观察图形可知,这组图形是6个图形一个循环,分别按照△△□□□〇的顺序依次排列,所以求出第?103个图形是第几个循环的第几个图形即可解答问题.
【解答】解:103÷6=17(个循环)…1个
所以第103个图形是第18循环的第一个图形,与第一个循环的第一个图形相同,是△.
所以原题”第103个图形是〇“说法错误.
故答案为:×.
【点评】本题考查图形排列的规律:认真找出哪些图形是一组是关键.
四.计算题(共3小题)
26.【分析】根据分数加减法的计算方法进行计算.
﹣( )=,求未知减数,用被减数减去差;
根据加法交换律和结合律进行简算.
【解答】解:
= 1= = ﹣=
= = = 1=
故答案为:.
【点评】口算时,注意运算符号和数据,然后再进一步计算.
27.【分析】对于一般的两个数来说,这两个数的公有质因数的连乘积是这两个数的最大公因数,这两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;当两个数成倍数关系,最大公因数为较小的数,较大的那个数,是这两个数的最小公倍数;是互质数的两个数,它们的最大公因数是1,最小公倍数即这两个数的乘积.
【解答】解:24=2×2×2×3
36=2×2×3×3
最大公约数是2×2×3=12,最小公倍数是2×2×2×3×3=72.
20=2×2×5,
15=3×5,
最大公因数是5,最小公倍数是2×2×3×5=60;
9和27是倍数关系,最大公约数是9,最小公倍数是27;
5和8是互质数,所以它们的最大公因数是1,最小公倍数是这两个数的乘积,5×8=40.
【点评】此题主要考查了求两个数的最大公因数和最小公倍数的方法:对于一般的两个数来说,这两个数的公有质因数的连乘积是这两个数的最大公因数,这两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;当两个数成倍数关系,最大公因数为较小的数,较大的那个数,是这两个数的最小公倍数;是互质数的两个数,它们的最大公因数是1,最小公倍数即这两个数的乘积.
28.【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,正方体的体积=棱长×棱长×棱长,由此代入数据即可解答.
【解答】解:长方体的表面积是:
(8×3+8×5+3×5)×2
=(24+40+15)×2
=79×2
=158(平方厘米)
正方体的体积是:5×5×5=125(立方厘米)
答:长方体的表面积是158平方厘米;正方体的体积是125立方厘米.
【点评】此题考查了长方体和正方体的表面积与体积公式的计算应用.
五.应用题(共5小题)
29.【分析】把两次用去的占得分率相加,就是两次一共用去了几分之几;把这条绳子看作单位“1”,用单位“1”减去两次用去占的分率和,就是还剩下的几分之几.
【解答】解: +=;
1﹣=.
答:两次共用去了它的,还剩.
【点评】此题考查分数加减法应用题以及同分数分数加减法的计算方法,要注意结果化成最简分数.
30.【分析】(1)根据折线统计图可知,跑完1000米,马军用了5分钟,王林用了4分钟,所以王林比赛赢了.;
(2)在起跑后的第1分钟,马军跑了400米,王林大约跑了280米,所以在起跑后的第1分,马军跑的速度快些;在起跑后的第3分钟,两人的折线相重合,此时两人跑的路程同样多,大约是800米;
(3)根据公式路程÷时间=速度进行计算即可得到答案.
【解答】解:(1)跑完1000米,马军用了5分钟,王林比赛赢了.
(2)起跑后的第1分钟,马军速度快一些.第3分钟,两人跑的路程相同,是800米.
(3)1000÷4=250(米)
答:王林的平均速度是米/分.
故答案为:5,王林,马军,3,800,250.
【点评】此题主要考查的是如何从折线统计图中获取信息,然后再根据信息进行分析、计算即可.
31.【分析】按4面红旗、3面黄旗依次不断的出现,是把4+3=7面红旗看成一个循环,用142除以7求出商和余数,再根据余数进行推算.
【解答】解:142÷(4+3)
=142÷7
=20……2
余数是2,所以第142面旗子是第21个循环的第2面,是红色的.
答:第142面彩旗是红色的.
【点评】解决这类问题关键是把重复出现的部分看成一组,根据除法的意义,求出总数量里面有多少个这样的一组,还余几,然后根据余数进行推算.
32.【分析】根据题意,玉米试验田占这块地的,水稻试验田占这块地的;说明和的单位“1”相同,比较这两个分数,分数大的占地面积大,由此判断即可.
【解答】解:=
=
所以<
答:水稻试验田的占地面积大.
【点评】解决本题先找清楚单位“1”是否相同,明确能否直接比较,再根据分数比较大小的方法求解.
33.【分析】首先要明确:升高的那部分水的体积就等于铁球的体积,因此需要先求出升高的水的高度,由原来有水5升,利用长方体的体积公式V=abh即可求出原来的水的高度,用现在的水的高度减去原来的水的高度,就是升高的水的高度,进而可以求出升高的那部分水的体积,问题即可得解.
【解答】解:5升=5立方分米
原来的水的高度:5÷(2×2)
=5÷4
=1.25(分米)
升高的水的高度:1.5﹣1.25=0.25(分米)
铁球的体积:2×2×0.25
=4×0.25
=1(立方分米)
答:这个铁球的体积是1立方分米.
【点评】此题主要考查长方体的体积的计算方法的实际应用,关键是明白:升高的那部分水的体积就等于铁球的体积,求出升高的水的高度,是解答本题的关键.
同课章节目录
