高中数学 选修1-1 用《几何画板》探究点的轨迹:椭圆 课件 21张PPT
文档属性
| 名称 | 高中数学 选修1-1 用《几何画板》探究点的轨迹:椭圆 课件 21张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-02 10:09:54 | ||
图片预览






文档简介
(共21张PPT)
四川省金堂中学 喻斌
人教A版普通高中课程标准实验教科书
数学选修1-1第二章2.1椭圆
用《几何画板》探究点的轨迹:椭圆
博学 广才 厚德 尚美
德国数学家开普勒发现行星
的轨道是椭圆形,成为历史上百个伟大发现之一。
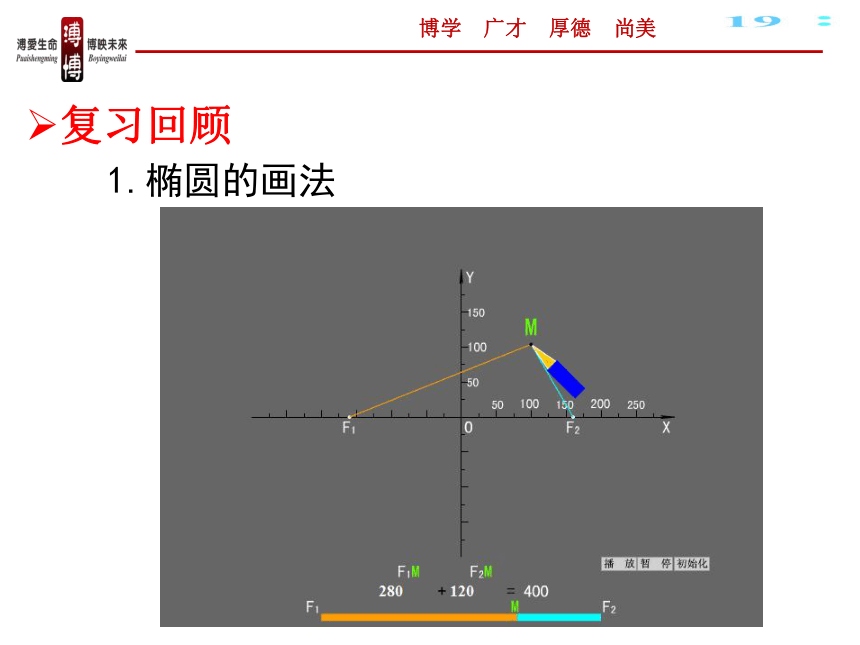
1.椭圆的画法
复习回顾
博学 广才 厚德 尚美
2.椭圆的定义
第一定义
复习回顾
博学 广才 厚德 尚美
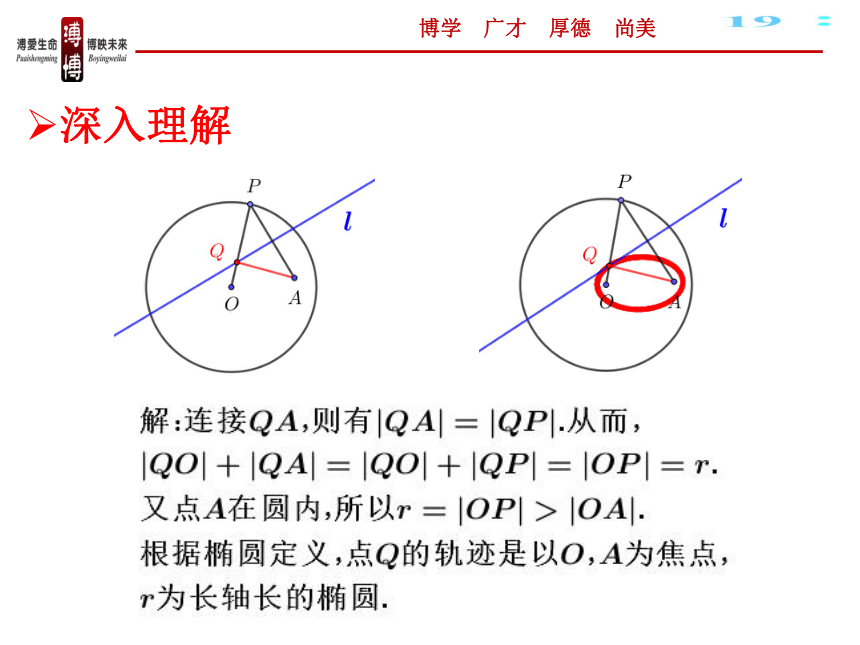
课本第42页习题2.1A组第7题
深入理解
【探究1】
博学 广才 厚德 尚美
深入理解
博学 广才 厚德 尚美
通过本题的解决,谈谈你对椭圆第一定义的理解。
归纳点拨
博学 广才 厚德 尚美
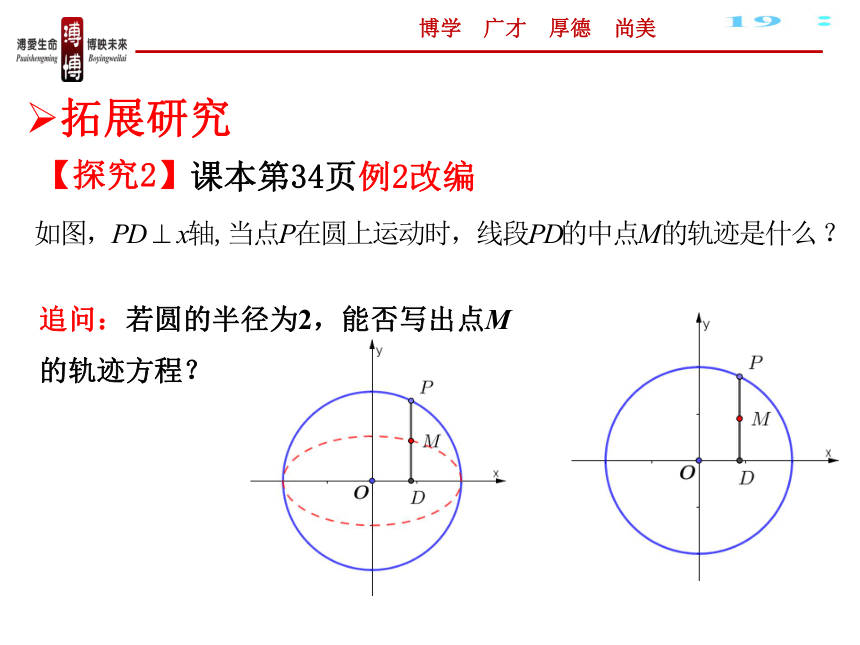
课本第34页例2改编
拓展研究
【探究2】
追问:若圆的半径为2,能否写出点M的轨迹方程?
博学 广才 厚德 尚美
课本第43页习题2.1B组第1题改编
类比探究
【探究3】
追问:若圆的半径为2,能否写出点M的轨迹方程?
博学 广才 厚德 尚美
通过这个两个例子,你有什么发现?
将圆按照某个方向均匀地压缩或拉伸,可以得到椭圆.
归纳点拨
博学 广才 厚德 尚美
拓展研究
【探究4】
博学 广才 厚德 尚美
追问:能否写出点M所成轨迹的参数方程与直角坐标方程?
合作探究
【探究4】
博学 广才 厚德 尚美
课本第41页例6
探究发现
【探究5】
博学 广才 厚德 尚美
抽象概括
博学 广才 厚德 尚美
抽象概括
博学 广才 厚德 尚美
根据以上探究发现,请你抽象概括一下,给椭圆下一个新的定义!
抽象概括
博学 广才 厚德 尚美
椭圆第二定义:
抽象概括
博学 广才 厚德 尚美
探究点的轨迹---椭圆
第一定义
伸缩法
第二定义
?
参数方程法
总结提高
巧用几何画板
博学 广才 厚德 尚美
1.你可以独立完成下列任务吗?
用类似的方法探究点的轨迹--双曲线、抛物线!
2.继续坚持:在学习数学的过程中,学会欣赏数学,应用数学,体验魅力无穷的数学之美!
课后作业
博学 广才 厚德 尚美
给同学们的建议:
学习信息技术;
自己动手作图;
开展数学实验;
观察数学现象;
发现数学结论;
解决数学问题。
博学 广才 厚德 尚美
谢谢!
博学 广才 厚德 尚美
四川省金堂中学 喻斌
人教A版普通高中课程标准实验教科书
数学选修1-1第二章2.1椭圆
用《几何画板》探究点的轨迹:椭圆
博学 广才 厚德 尚美
德国数学家开普勒发现行星
的轨道是椭圆形,成为历史上百个伟大发现之一。
1.椭圆的画法
复习回顾
博学 广才 厚德 尚美
2.椭圆的定义
第一定义
复习回顾
博学 广才 厚德 尚美
课本第42页习题2.1A组第7题
深入理解
【探究1】
博学 广才 厚德 尚美
深入理解
博学 广才 厚德 尚美
通过本题的解决,谈谈你对椭圆第一定义的理解。
归纳点拨
博学 广才 厚德 尚美
课本第34页例2改编
拓展研究
【探究2】
追问:若圆的半径为2,能否写出点M的轨迹方程?
博学 广才 厚德 尚美
课本第43页习题2.1B组第1题改编
类比探究
【探究3】
追问:若圆的半径为2,能否写出点M的轨迹方程?
博学 广才 厚德 尚美
通过这个两个例子,你有什么发现?
将圆按照某个方向均匀地压缩或拉伸,可以得到椭圆.
归纳点拨
博学 广才 厚德 尚美
拓展研究
【探究4】
博学 广才 厚德 尚美
追问:能否写出点M所成轨迹的参数方程与直角坐标方程?
合作探究
【探究4】
博学 广才 厚德 尚美
课本第41页例6
探究发现
【探究5】
博学 广才 厚德 尚美
抽象概括
博学 广才 厚德 尚美
抽象概括
博学 广才 厚德 尚美
根据以上探究发现,请你抽象概括一下,给椭圆下一个新的定义!
抽象概括
博学 广才 厚德 尚美
椭圆第二定义:
抽象概括
博学 广才 厚德 尚美
探究点的轨迹---椭圆
第一定义
伸缩法
第二定义
?
参数方程法
总结提高
巧用几何画板
博学 广才 厚德 尚美
1.你可以独立完成下列任务吗?
用类似的方法探究点的轨迹--双曲线、抛物线!
2.继续坚持:在学习数学的过程中,学会欣赏数学,应用数学,体验魅力无穷的数学之美!
课后作业
博学 广才 厚德 尚美
给同学们的建议:
学习信息技术;
自己动手作图;
开展数学实验;
观察数学现象;
发现数学结论;
解决数学问题。
博学 广才 厚德 尚美
谢谢!
博学 广才 厚德 尚美
