高中数学选修1-1第二章圆锥曲线与方程阅读与思考 圆锥曲线的光学性质及其应用 课件 25张PPT
文档属性
| 名称 | 高中数学选修1-1第二章圆锥曲线与方程阅读与思考 圆锥曲线的光学性质及其应用 课件 25张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-02 10:10:31 | ||
图片预览







文档简介
(共25张PPT)
课程名称:圆锥曲线的光学性质及其应用
教材版本:人民教育出版社A版选修1-1
工作单位:四川省成都市铁路中学校
看一看
请观看一段视频,了解黑洞照片背后的八大“功臣”
拍摄黑洞的射电望远镜反射镜面为抛物面。
在这个椭圆球桌上,如何击球,能使小球进洞?
看一看
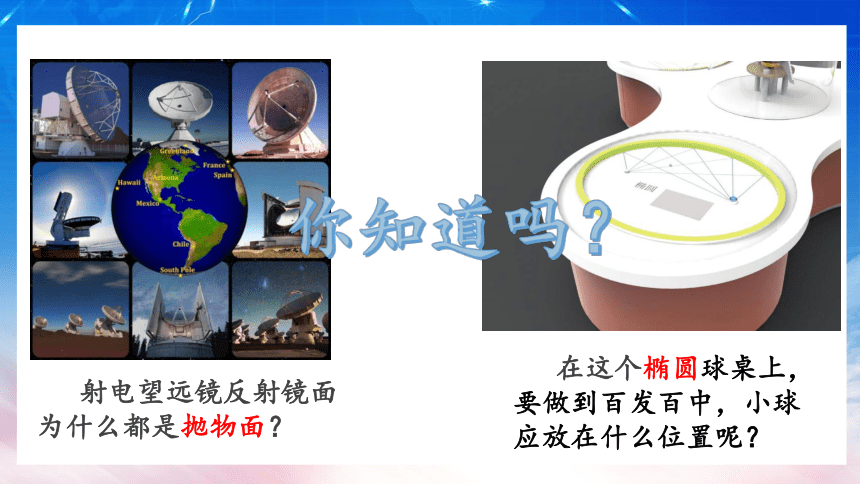
在这个椭圆球桌上,要做到百发百中,小球应放在什么位置呢?
你知道吗?
射电望远镜反射镜面为什么都是抛物面?
圆锥曲线的光学性质及其应用
请阅读与思考教材第65页的内容
你有哪些收获?
读一读
椭圆的光学性质:
从椭圆的一个焦点发出的光线,经过椭圆反射后,反射光线交于椭圆的另一个焦点上
抛物线的光学性质:
从抛物线的焦点发出的光线,经过抛物线反射后,反射光线平行于抛物线的轴。
双曲线的光学性质:
从双曲线的一个焦点发出的光,经过双曲线反射后,反射光线的反向延长线都汇聚到双曲线的另一个焦点上.
圆锥曲线为什么具有如此奇妙的性质呢?
圆锥曲线的光学性质
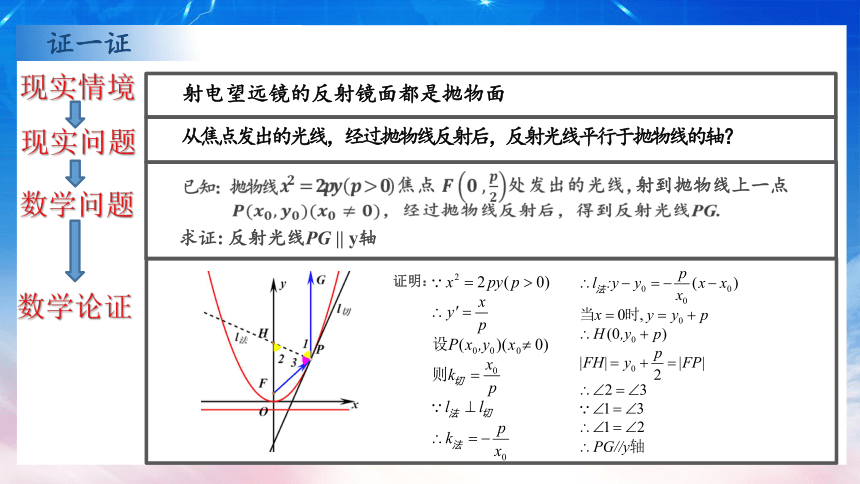
从焦点发出的光线,经过抛物线反射后,反射光线平行于抛物线的轴?
现实问题
数学问题
数学论证
,经过抛物线反射后,得到反射光线PG.
求证: 反射光线PG || y轴
射到抛物线上一点
证一证
现实情境
射电望远镜的反射镜面都是抛物面
证明:
说一说
你能解释课首的两个现象中蕴含的奥秘吗?
在椭圆球桌上,要做到百发百中,小球应放在什么位置呢?
射电望远镜反射镜面为什么都是抛物面?
说一说
如果是抛物线球桌,是否也能百发百中呢?为什么?
图中,两条抛物线的轴重合,并且它们关于焦点连线的中点对称。
如果是双曲线球桌,是否还能百发百中呢?为什么?
说一说
古希腊时代,西西里岛上有一个椭圆形岩洞监狱。被关押的犯人秘密商讨逃跑的计划,可每次的逃跑计划都会很快被看守知道。犯人们百思不得其解,以为内部出现了内奸,其实并非有内奸,而是山洞的形状有奥妙。你能解开这个谜吗?
说一说
聪明的同学们,你还能说出圆锥曲线的光学性质在生活中的哪些妙用呢?
说一说
手电筒
太阳灶
电影放映机
奥运圣火采集器
1.如图,已知手电筒反光碗的轴截面轮廓是抛物线y2=8x ,焦点F发出的一条光线经抛物线上一点P反射后过点Q,若点Q的纵坐标为4,则点P的坐标= .
做一做
2.已知点P是椭圆C:上除长轴端点外的任一点,连接设的角平分线PM交C的长轴于M(m,0),则m的取值范围是 .
做一做
3.已知l1,l2分别是椭圆双曲线在交点A处的切线,设这两条直线的斜率分别为k1,k2则k1k2= .
做一做
-1
独立思考
小组合作
分享交流
通过本节课的学习,你有哪些收获?
悟一悟
(3)你能将圆锥曲线的光学性质进行组合,尝试设计一些作品吗?
(2)在圆锥曲线中能不能找到其它的光学性质?有没有其它的曲线也具有很好的光学性质?
悟一悟
请同学们课后继续思考:
(1)如果不是从圆锥曲线焦点发出的光,经圆锥曲线反射后会怎样呢?
感谢您的观看!
课程名称:圆锥曲线的光学性质及其应用
教材版本:人民教育出版社A版选修1-1
工作单位:四川省成都市铁路中学校
看一看
请观看一段视频,了解黑洞照片背后的八大“功臣”
拍摄黑洞的射电望远镜反射镜面为抛物面。
在这个椭圆球桌上,如何击球,能使小球进洞?
看一看
在这个椭圆球桌上,要做到百发百中,小球应放在什么位置呢?
你知道吗?
射电望远镜反射镜面为什么都是抛物面?
圆锥曲线的光学性质及其应用
请阅读与思考教材第65页的内容
你有哪些收获?
读一读
椭圆的光学性质:
从椭圆的一个焦点发出的光线,经过椭圆反射后,反射光线交于椭圆的另一个焦点上
抛物线的光学性质:
从抛物线的焦点发出的光线,经过抛物线反射后,反射光线平行于抛物线的轴。
双曲线的光学性质:
从双曲线的一个焦点发出的光,经过双曲线反射后,反射光线的反向延长线都汇聚到双曲线的另一个焦点上.
圆锥曲线为什么具有如此奇妙的性质呢?
圆锥曲线的光学性质
从焦点发出的光线,经过抛物线反射后,反射光线平行于抛物线的轴?
现实问题
数学问题
数学论证
,经过抛物线反射后,得到反射光线PG.
求证: 反射光线PG || y轴
射到抛物线上一点
证一证
现实情境
射电望远镜的反射镜面都是抛物面
证明:
说一说
你能解释课首的两个现象中蕴含的奥秘吗?
在椭圆球桌上,要做到百发百中,小球应放在什么位置呢?
射电望远镜反射镜面为什么都是抛物面?
说一说
如果是抛物线球桌,是否也能百发百中呢?为什么?
图中,两条抛物线的轴重合,并且它们关于焦点连线的中点对称。
如果是双曲线球桌,是否还能百发百中呢?为什么?
说一说
古希腊时代,西西里岛上有一个椭圆形岩洞监狱。被关押的犯人秘密商讨逃跑的计划,可每次的逃跑计划都会很快被看守知道。犯人们百思不得其解,以为内部出现了内奸,其实并非有内奸,而是山洞的形状有奥妙。你能解开这个谜吗?
说一说
聪明的同学们,你还能说出圆锥曲线的光学性质在生活中的哪些妙用呢?
说一说
手电筒
太阳灶
电影放映机
奥运圣火采集器
1.如图,已知手电筒反光碗的轴截面轮廓是抛物线y2=8x ,焦点F发出的一条光线经抛物线上一点P反射后过点Q,若点Q的纵坐标为4,则点P的坐标= .
做一做
2.已知点P是椭圆C:上除长轴端点外的任一点,连接设的角平分线PM交C的长轴于M(m,0),则m的取值范围是 .
做一做
3.已知l1,l2分别是椭圆双曲线在交点A处的切线,设这两条直线的斜率分别为k1,k2则k1k2= .
做一做
-1
独立思考
小组合作
分享交流
通过本节课的学习,你有哪些收获?
悟一悟
(3)你能将圆锥曲线的光学性质进行组合,尝试设计一些作品吗?
(2)在圆锥曲线中能不能找到其它的光学性质?有没有其它的曲线也具有很好的光学性质?
悟一悟
请同学们课后继续思考:
(1)如果不是从圆锥曲线焦点发出的光,经圆锥曲线反射后会怎样呢?
感谢您的观看!
