苏科版数学七年级(下)第10章《二元一次方程组》教学质量检测卷(含答案)
文档属性
| 名称 | 苏科版数学七年级(下)第10章《二元一次方程组》教学质量检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 206.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-31 09:01:10 | ||
图片预览




文档简介
苏科版七年级(下)第10章《二元一次方程组》教学质量检测卷
满分100分,时间80分钟
姓名__________座号__________成绩__________
一.选择题(共8小题,满分24分)
1.若方程(a+3)x+3y|a|﹣2=1是关于x,y的二元一次方程,则a的值为( )
A.﹣3 B.±2 C.±3 D.3
2.解下面的方程组时,要使解法较为简便,应( )
A.先消去x B.先消去y C.先消去z D.先消去常数
3.是下列哪个方程的一个解( )
A.﹣2x+y=﹣3 B.3x+y=6 C.6x+y=8 D.﹣x+y=1
4.某次知识竞赛共有20道题,规定:每答对一道题得+5分,每答错一道题得﹣2分,不答的题得0分,已知圆圆这次竞赛得了60分,设圆圆答对了x道题,答错了y道题,则( )
A.x﹣y=20 B.x+y=20 C.5x﹣2y=60 D.5x+2y=60
5.如果方程组与有相同的解,则a,b的值是( )
A. B. C. D.
6.商店里有A、B、C三种商品,单价分别为50元,30元,10元.若小明购买了两种商品,共花费140元,则小明的购买方案有( )种.
A.3 B.7 C.10 D.12
7.如果方程组的解是二元一次方程3x﹣5y﹣30=0的一个解,那么m的值为( )
A.7 B.6 C.3 D.2
8.某校九年级师生共466人,准备组织去某地参加综合社会实践活动.现已预备了37座和49座两种客车共10辆,刚好坐满.设37座客车a辆,49座客车b辆,根据题意可列出方程组为( )
A.B.C.D.
二.填空题(共8小题,满分24分)
9.已知二元一次方程2x﹣y=3,用含x的式子表示y的形式是 .
10.方程组是关于x,y的二元一次方程组,则ab的值是 .
11.已知|x+y+2|+(2x﹣3y﹣1)2=0,则x+y= .
12.若关于x,y的方程组有正整数解,则整数k的值是 .
13.小明去文具店购买了5只黑色碳素笔和3个修正带,一共花费74元,其中黑色碳素笔的单价比修正带的单价多2元,求黑色碳素笔的单价和修正带的单价.设黑色碳素笔的单价为x元,修正带的单价为y元,依题意可列方程组为 .
14.为实现营养的合理搭配,某电商推出适合不同人群的甲、乙两种袋装混合粗粮.其中,甲种袋装粗粮每袋装有3千克A粗粮,1千克B粗粮,1千克C粗粮;乙种袋装粗粮每袋装有1千克A粗粮,2千克B粗粮,2千克C粗粮.甲、乙两种袋装粗粮每袋成本价分别为袋中的A、B、C三种粗粮的成本价之和.已知A粗粮每千克成本价为6元,甲种粗粮每袋售价为71.5元,利润率为30%,乙种粗粮利润率为20%,则乙种粗粮每袋的售价为 元.(利润率=×100%)
15.对于x,y,定义新运算x?y=ax+by﹣3(其中a,b是常数),等式的右边是通常的加法与乘法运算,已知1?2=9,(﹣3)?3=6,则2?(﹣7)= .
16.如图所示的各图表示由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案花盆的总数为s,按此规律推断,以s,n为未知数的二元一次方程为s= .
三.解答题(共8小题,满分52分)
17.解方程组
(1) (2).
18.解三元一次方程组:.
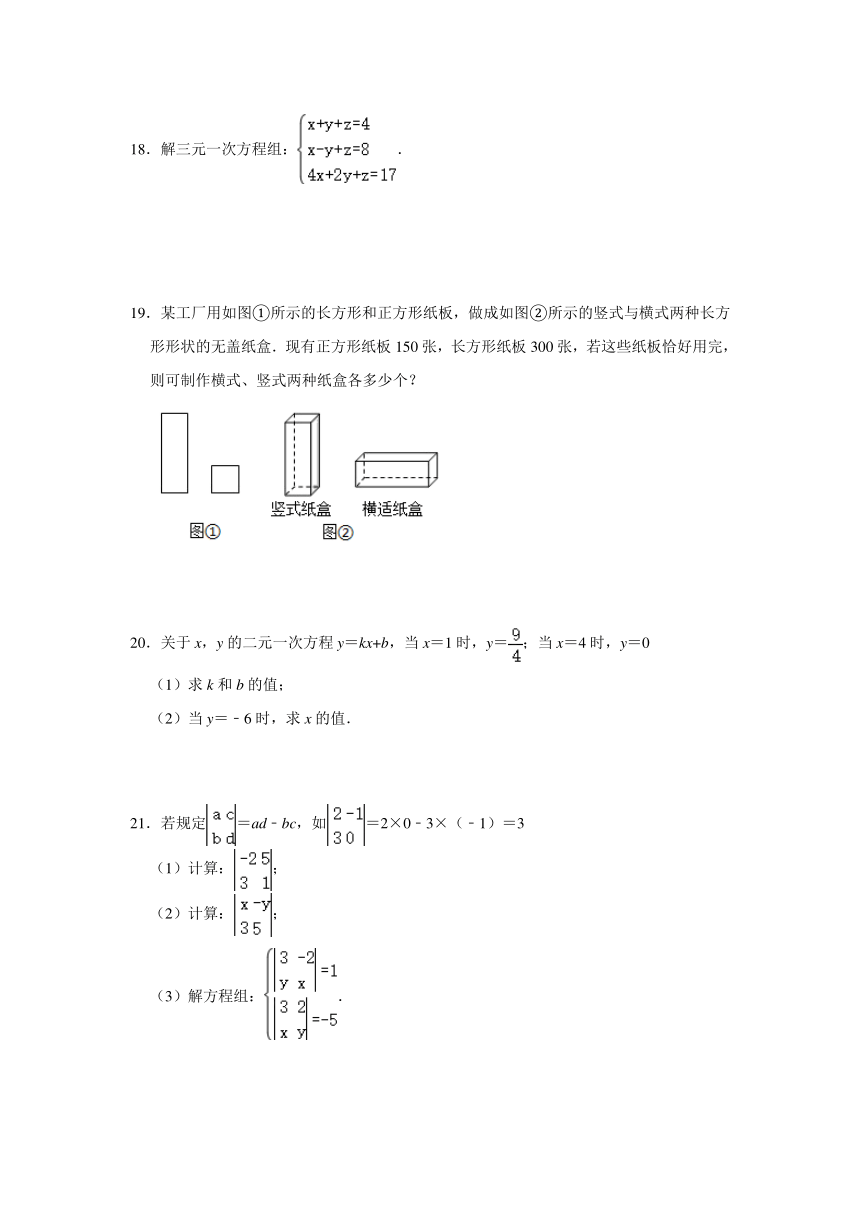
19.某工厂用如图①所示的长方形和正方形纸板,做成如图②所示的竖式与横式两种长方形形状的无盖纸盒.现有正方形纸板150张,长方形纸板300张,若这些纸板恰好用完,则可制作横式、竖式两种纸盒各多少个?
20.关于x,y的二元一次方程y=kx+b,当x=1时,y=;当x=4时,y=0
(1)求k和b的值;
(2)当y=﹣6时,求x的值.
21.若规定=ad﹣bc,如=2×0﹣3×(﹣1)=3
(1)计算:;
(2)计算:;
(3)解方程组:.
22.有这样一个问题:已知,求a+b+c的值;小腾根据解二元一次方程组的经验,得到a+b+c=4,请你写出完整的解题过程.
23.小明同学遇到下面的问题解方程组,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错,如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题,以下是他的解题过程:令m=2x+3y,n=2x﹣3y,这时原方程组化为,解得,把代入m=2x+3y,n=2x﹣3y得,解得,所以,原方程组的解为.请你参考小明同学的做法,解决下面的问题:解方程组.
24.滨江区各学校积极参加“给贫困山区献爱心”活动,教育局筹集了120吨的衣物书籍等物品运往山区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 甲 乙 丙
汽车运载量(吨/辆) 5 8 10
汽车运费(元/辆) 200 250 300
(1)全部物资可用甲型车8辆,乙型车5量,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费4100元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,教育局打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
参考答案
一.选择题(共8小题)
1.【解答】解:∵方程(a+3)x+3y|a|﹣2=1是关于x,y的二元一次方程,
∴a+3≠0,|a|﹣2=1,
解得a=3.
故选:D.
2.【解答】解:由方程组知①中没有未知数z,只需利用加减法消去②、③中的z求解较为简便,
故选:C.
3.【解答】解:将分别代入四个选项:
﹣2×2+1=﹣3,故A选项正确;
3×2+1=7,故B选项不正确;
6×2+1=13,故C选项不正确;
﹣2+1=﹣1,故D选项不正确;
故选:A.
4.【解答】解:设圆圆答对了x道题,答错了y道题,
依题意得:5x﹣2y+(20﹣x﹣y)×0=60.
故选:C.
5.【解答】解:由已知得方程组,
解得,
代入,
得到,
解得.故选:A.
6.【解答】解:①设A种商品买x件,B种商品买y件,
由题意得:50x+30y=140
∵x、y都是正整数
∴,
②设A种商品买a件,C种商品买b件;
由题意得:50a+10b=140
∵a、b都是正整数
∴,.
③设B种商品买m件,C种商品买n件,
由题意得:30m+10n=140
∵m、n都是正整数
∴,,,.
综合以上可得小明的购买方案有7种.
故选:B.
7.【解答】解:,
①+②得:2x=5m,
解得:x=2.5m,
①﹣②得:2y=﹣3m,
解得:y=﹣1.5m,
代入3x﹣5y﹣30=0得:7.5m+7.5m﹣30=0,
解得:m=2,
故选:D.
8.【解答】解:设37座客车a辆,49座客车b辆,
依题意,得:.
故选:A.
二.填空题(共8小题)
9.【解答】解:∵2x﹣y=3,
∴y=2x﹣3,
故答案为:y=2x﹣3.
10.【解答】解:由题意得:|a|=1,b﹣5=0,a﹣1≠0,
解得:a=﹣1,b=5,
则原式=(﹣1)5=﹣1.
故答案为:﹣1.
11.【解答】解:∵|x+y+2|+(2x﹣3y﹣1)2=0,
∴,
①×3+②得:5x=﹣5,即x=﹣1,
把x=﹣1代入①得:y=﹣1,
则x+y=﹣1﹣1=﹣2,
故答案为:﹣2
12.【解答】解:,
由②得:x=2y,代入①得:4y+ky=3,
则y=,
∵原方程组有正整数解,
∴则4+k=1或4+k=3,
解得:k=﹣3或k=﹣1.
故答案为:﹣3或﹣1.
13.【解答】解:由题意可得,
,
故答案为:.
14.【解答】解:设B粗粮每千克的成本价为x元,C粗粮每千克的成本价为y元,乙种粗粮每袋售价为z元,
依题意,得:,
解得:.
故答案为:96.
15.【解答】解:根据题意,得:,
整理,得:,
①﹣②,得:3b=15,
解得:b=5,
将b=5代入①,得:a+10=12,
解得:a=2,
∴x?y=2x+5y﹣3,
则2?(﹣7)=2×2+5×(﹣7)﹣3=4﹣35﹣3=﹣34,
故答案为:﹣34.
16.【解答】解:根据图案组成的是三角形的形状,则其周长等于边长的3倍,
所以s=3(n﹣1).
故答案为:3(n﹣1).
三.解答题(共8小题)
17.【解答】解:(1),
把①代入②得:3x+2x﹣4=1,
解得:x=1,
把x=1代入①得:y=﹣2,则方程组的解为;
(2)方程组整理得:,
①×2﹣②得:3y=9,
解得:y=3,
把y=3代入②得:x=5,则方程组的解为.
18.【解答】解:
②﹣①得:﹣2y=4,
解得:y=﹣2,
把y=﹣2代入①得:x﹣2+z=4,
即x+z=6④,
把y=﹣2代入③得:4x﹣4+z=17,
即4x+z=21⑤,
由④和⑤组成一个二次一次方程组,解得:,
所以原方程组的解是:.
19.【解答】解:设制作竖式纸盒x个,则生产横式纸盒y个.
由题意得,解得:.
答:可制作横式纸盒60个、竖式纸盒30个.
20.【解答】解:(1)把x=1,y=;x=4,y=0代入得:,解得:;
(2)由(1)得:y=﹣x+3,
把y=﹣6代入得:﹣6=﹣x+3,解得:x=12.
21.【解答】解:(1)∵=ad﹣bc,
∴原式=﹣2﹣15
=﹣17;
(2)原式=5x+3y;
(3)由题意可得,解得.
22.【解答】解:,
①﹣②,得(a﹣c)(x2﹣y2)=0,
∵a≠c,
∴x2﹣y2=0,
∴(x+y)(x﹣y)=0,
∵x+y=1,
∴x﹣y=0,
由,解得:x=y=,
把x=y=代入①,得a+b+c=4.
23.【解答】解:由题意可设x+y=m,x﹣y=n,
则方程组变形为,解得:,
∴,
解得:.
24.【解答】解:(1)根据题意得:
(120﹣5×8﹣5×8)÷10=4(辆),
答:丙型车需4辆来运送.
故答案为:4.
(2)设需要甲x辆,乙y辆,根据题意得:
,
解得:,
答:分别需甲、乙两种车型为8辆和10辆.
(3)设甲车有a辆,乙车有b辆,则丙车有(14﹣a﹣b)辆,由题意得
5a+8b+10(14﹣a﹣b)=120,
即a=4﹣b,
∵a、b、14﹣a﹣b均为正整数,
∴b只能等于5,从而a=2,14﹣a﹣b=7,
∴甲车2辆,乙车5辆,丙车7辆,
则需运费200×2+250×5+300×7=3750(元),
答:甲车2辆,乙车5辆,丙车7辆,需运费3750元.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
