六年级下册数学课件-第4单元 第2课时 比例的意义苏教版(共24张PPT)
文档属性
| 名称 | 六年级下册数学课件-第4单元 第2课时 比例的意义苏教版(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 19.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-31 15:51:21 | ||
图片预览








文档简介
课件24张PPT。新授课件苏教版数学
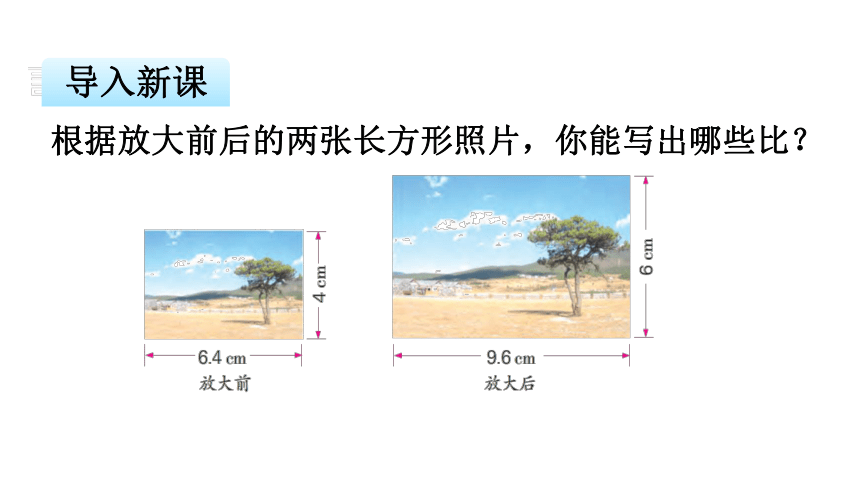
六年级下册 第四单元比 例 的 意 义导入新课 一张长方形的照片长6.4厘米,宽4厘米,把它按一定比放大后变成长为9.6厘米,你知道它是按( ):( )的比放大的吗?放大后的宽应是多少?4×1.5=6(厘米)9.6:6.4=3:2它是按3:2的比放大的。放大后的宽是6厘米。导入新课根据放大前后的两张长方形照片,你能写出哪些比?探究新知(1)放大前的照片长和宽的比是6.4:4。
(2)放大后的照片长和宽的比9.6:6。
(3)放大后与放大前长的比是9.6:6.4。
(4)放大后与放大前宽的比是6:4。猜一猜:哪两个比之间可能存在关系?探究新知小组讨论:
1.两个比之间存在的关系,并说一说是怎样判断的?
2.可以分别求出它们的比值,或把它们分别化简。探究新知6.4:4=9.6:6 或 =像这样表示两个比相等的式子叫作比例。巩固练习1. 哪几组的两个比可以组成比例? 把组成的比例写出来。
(1) 10:12 和 25:30 (2) 2:8 和 9:27(3) 0.9:3 和 15:115 (4) : 和 :10:12 = 25:30 巩固练习2. 商场开展促销活动, 所有商品一律八折优惠。50 : 40 = 200 : 160 (答案不唯一)巩固练习3. 一辆汽车上午 4 小时行驶 320 千米, 下午 3 小时行驶 240 千米。
(1) 上午行驶的路程和时间的比是几比几? 下午呢? 这两个比能组成比例吗? 为什么?上午行驶的路程和时间的比是320 : 4,下午行驶的路程和时间的比是240 : 3。
这两个比能组成比例,因为320 : 4 = 4: 3。巩固练习3. 一辆汽车上午 4 小时行驶 320 千米, 下午 3 小时行驶 240 千米。
(2) 上、 下午行驶路程的比和上、 下午行驶时间的比也能组成比例吗?320 : 240 = 4 : 3,上、 下午行驶路程的比和上、 下午行驶时间的比能组成比例。巩固练习4. 判断下面哪个比能与 : 4 组成比例。
(1) 5:4 (2) 20:1 (3) 1:20 (4) 5: 1 : 20 = : 4巩固练习5. 李梅为了布置教室墙报, 剪了三张大小不同的长方形剪纸。(1)写出每张长方形剪纸长与宽的比,并算出比值。15:10=3:2=18:12=3:2=24:16=3:2=巩固练习5. 李梅为了布置教室墙报, 剪了三张大小不同的长方形剪纸。15 :10 = 18 : 12 (2)选择其中的两个比组成比例。巩固练习下面各表中相对应的两个数量的比能否组成比例?如果能组成比例, 把组成的比例写出来。240:4=360:6 20:5=28:7 2.1:3=3.5:5 不能组成比例巩固练习观察下面的两幅图, 左图中的两个长方形有什么关系? 右图中的两个平行四边形呢?左图中的小长方形按比例放大得到大长方形, 右图中的小平行四边形按比例放大得到大平行四边形。巩固练习你能照样子分别把下面的三角形和四边形按 2:1 的比放大吗?拓展练习1. 从12的因数中任意选出4个数,组成两个比例。( 1 ):( 2 )=( 3 ):( 6 )12的因数:1、2、3、4、6、12( 2 ):( 3 )=( 4 ):( 6 ) …… 拓展练习2. 某日上午,阳光下人高1.5米,影长1.2米;树高3.5米,影长2.8米。分别求出人高和影长的比、树高和影长的比。它们能组成比例吗?人高:影长=1.5:1.2=人高:影长=树高:影长 1.5:1.2=3.5:2.8比值相等,所以能组成比例。课堂总结表示两个比相等的式子叫作比例。数学阅读 阿基米德有许多故事,其中最着名的要算发现阿基米德定律的那个洗澡的故事了。
国王做了一顶金王冠,他怀疑工匠用银子偷换了一部分金子,便要阿基米德鉴定它是不是纯金制的,且不能损坏王冠。阿基米德捧着这顶王冠整天苦苦思索,有一天,阿基米德去浴室洗澡,他跨入浴桶,随着身子浸入浴桶,一部分水就从桶边溢出,阿基米德看到这个现象,头脑中像闪过一道闪电,“我找到了!”他兴奋地大喊道。
数学阅读 阿基米德拿一块金块和一块质量相等的银块,分别放入一个盛满水的容器中,发现银块排出的水多得多。于是阿基米德拿了与王冠质量相等的金块,放入盛满水的容器里,测出排出的水量;再把王冠放入盛满水的容器里,看看排出的水量是否一样,问题就解决了。随着进一步研究,沿用至今的流体力学最重要基石——阿基米德定律诞生了。
(2)放大后的照片长和宽的比9.6:6。
(3)放大后与放大前长的比是9.6:6.4。
(4)放大后与放大前宽的比是6:4。猜一猜:哪两个比之间可能存在关系?探究新知小组讨论:
1.两个比之间存在的关系,并说一说是怎样判断的?
2.可以分别求出它们的比值,或把它们分别化简。探究新知6.4:4=9.6:6 或 =像这样表示两个比相等的式子叫作比例。巩固练习1. 哪几组的两个比可以组成比例? 把组成的比例写出来。
(1) 10:12 和 25:30 (2) 2:8 和 9:27(3) 0.9:3 和 15:115 (4) : 和 :10:12 = 25:30 巩固练习2. 商场开展促销活动, 所有商品一律八折优惠。50 : 40 = 200 : 160 (答案不唯一)巩固练习3. 一辆汽车上午 4 小时行驶 320 千米, 下午 3 小时行驶 240 千米。
(1) 上午行驶的路程和时间的比是几比几? 下午呢? 这两个比能组成比例吗? 为什么?上午行驶的路程和时间的比是320 : 4,下午行驶的路程和时间的比是240 : 3。
这两个比能组成比例,因为320 : 4 = 4: 3。巩固练习3. 一辆汽车上午 4 小时行驶 320 千米, 下午 3 小时行驶 240 千米。
(2) 上、 下午行驶路程的比和上、 下午行驶时间的比也能组成比例吗?320 : 240 = 4 : 3,上、 下午行驶路程的比和上、 下午行驶时间的比能组成比例。巩固练习4. 判断下面哪个比能与 : 4 组成比例。
(1) 5:4 (2) 20:1 (3) 1:20 (4) 5: 1 : 20 = : 4巩固练习5. 李梅为了布置教室墙报, 剪了三张大小不同的长方形剪纸。(1)写出每张长方形剪纸长与宽的比,并算出比值。15:10=3:2=18:12=3:2=24:16=3:2=巩固练习5. 李梅为了布置教室墙报, 剪了三张大小不同的长方形剪纸。15 :10 = 18 : 12 (2)选择其中的两个比组成比例。巩固练习下面各表中相对应的两个数量的比能否组成比例?如果能组成比例, 把组成的比例写出来。240:4=360:6 20:5=28:7 2.1:3=3.5:5 不能组成比例巩固练习观察下面的两幅图, 左图中的两个长方形有什么关系? 右图中的两个平行四边形呢?左图中的小长方形按比例放大得到大长方形, 右图中的小平行四边形按比例放大得到大平行四边形。巩固练习你能照样子分别把下面的三角形和四边形按 2:1 的比放大吗?拓展练习1. 从12的因数中任意选出4个数,组成两个比例。( 1 ):( 2 )=( 3 ):( 6 )12的因数:1、2、3、4、6、12( 2 ):( 3 )=( 4 ):( 6 ) …… 拓展练习2. 某日上午,阳光下人高1.5米,影长1.2米;树高3.5米,影长2.8米。分别求出人高和影长的比、树高和影长的比。它们能组成比例吗?人高:影长=1.5:1.2=人高:影长=树高:影长 1.5:1.2=3.5:2.8比值相等,所以能组成比例。课堂总结表示两个比相等的式子叫作比例。数学阅读 阿基米德有许多故事,其中最着名的要算发现阿基米德定律的那个洗澡的故事了。
国王做了一顶金王冠,他怀疑工匠用银子偷换了一部分金子,便要阿基米德鉴定它是不是纯金制的,且不能损坏王冠。阿基米德捧着这顶王冠整天苦苦思索,有一天,阿基米德去浴室洗澡,他跨入浴桶,随着身子浸入浴桶,一部分水就从桶边溢出,阿基米德看到这个现象,头脑中像闪过一道闪电,“我找到了!”他兴奋地大喊道。
数学阅读 阿基米德拿一块金块和一块质量相等的银块,分别放入一个盛满水的容器中,发现银块排出的水多得多。于是阿基米德拿了与王冠质量相等的金块,放入盛满水的容器里,测出排出的水量;再把王冠放入盛满水的容器里,看看排出的水量是否一样,问题就解决了。随着进一步研究,沿用至今的流体力学最重要基石——阿基米德定律诞生了。
