人教版数学八年级下册第17章:勾股定理的应用培优练习(附详细答案)
文档属性
| 名称 | 人教版数学八年级下册第17章:勾股定理的应用培优练习(附详细答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 226.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-31 00:00:00 | ||
图片预览




文档简介
人教版八年级下册第17章:勾股定理的应用培优练习
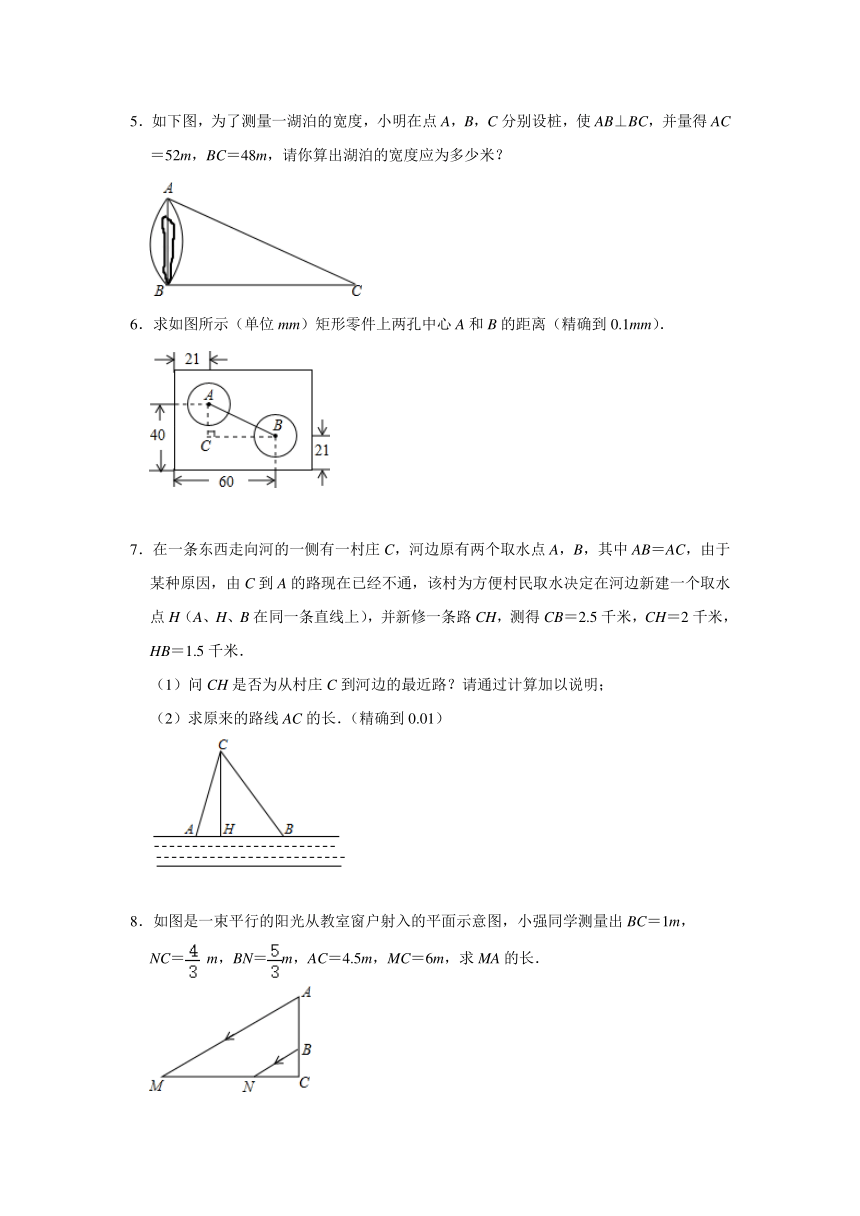
1.如图,马路边一根电线杆为5.4m,被一辆卡车从离地面1.5m处撞断,倒下的电线杆顶部是否会落在离它的底部4m的快车道上?
2.如图,一辆卡车装满货物后,能否通过如图所示的工厂厂门(上方为半圆)已知卡车高为3.0米,宽为1.6米,说明你的理由.
3.如图,是一个长8m,宽6m,高5m的仓库,在其内壁的A(长的四等分点)处有一只壁虎,B(宽的三等分点)处有一只蚊子,则壁虎爬到蚊子处的最短距离为多少米.
4.如下图,一个工人拿一个2.5米长的梯子,一头放在离墙0.7米处,另一头靠墙,如果梯子的顶部滑下0.4米,梯子的底部向外滑出多远?
5.如下图,为了测量一湖泊的宽度,小明在点A,B,C分别设桩,使AB⊥BC,并量得AC=52m,BC=48m,请你算出湖泊的宽度应为多少米?
6.求如图所示(单位mm)矩形零件上两孔中心A和B的距离(精确到0.1mm).
7.在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=2.5千米,CH=2千米,HB=1.5千米.
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明;
(2)求原来的路线AC的长.(精确到0.01)
8.如图是一束平行的阳光从教室窗户射入的平面示意图,小强同学测量出BC=1m,
NC= m,BN=m,AC=4.5m,MC=6m,求MA的长.
9.如图,一轮船以16n mi1e/h的速度从港口A出发向东北方向航行,另一轮船以12n mi1e/h的速度同时从港口出发向东南方向航行,那么离开港口A2h后,两船相距多远?
10.如图是一个塑料大棚,它的宽a=4.8m,高b=3.6m,棚总长d=10m.
(1)求大棚的占地面积.
(2)覆盖在顶上的塑料布需要多少平方米?
11.由于水资源缺乏,B,C两地不得不从黄河上的扬水站A处引水,这就需要在A,B,C之间铺设地下输水管道.有人设计了3种铺设方案(图中实线表示管道铺设线路).在图(2)中,AD⊥BC于点D,且BC=DC;在图(3)中,OA=OB=OC,且AO的延长线交BC于点E,AE⊥BC,BE=EC,OE=.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短.若△ABC恰好是一个边长为a的等边三角形,请你通过计算,判断哪一个铺设方案最好.
12.如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
13.如图,公路MN和公路PQ在点P处交汇,点A处有一所中学,且A点到MN的距离是米,假设拖拉机行驶时,周围100米以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时.
(1)学校是否会受到噪声影响?如果受影响,说明理由;
(2)已知拖拉机的速度为18千米/时,那么学校受影响的时间为多少秒?
14.在学习“神秘的数组”的课堂上,老师请同学们判断以3、4、5为边长的三角形是否为直角三角形时,小明是这样回答的:因为42+52=41,32=9,42+52≠32,所以以3、4、5为边长的三角形不是直角三角形.如果当时你也在课堂上,你的意见是什么?并说出你这样回答的理由.
15.如图,学校有一块空地ABCD,准备种草皮绿化已知∠ADC=90°,AD=4米,CD=3米,AB=13米,BC=12米,求这块地的面积.
16.在某段限速公路BC上(公路视为直线),交通管理部门规定汽车的最高行驶速度不能超过60km/h(即m),并在离该公路100m处设置了一个监测点A,在如图的平面直角坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上,另外一条公路在y轴上,AO为其中的一段.
(1)求点B和点C的坐标.
(2)一辆汽车从点B匀速行驶到点C所用时间是15s,判断一下这辆汽车在这段限速路上是否超速(取1.7)
17.如图,一个长为5m的梯子斜靠在墙上,梯子的底端距墙4m.
(1)求梯子的顶端距地面的垂直距离;
(2)若将梯子的底端向墙推进1m,求梯子的顶端升高了多少米;
(3)若使梯子的顶端距地面4.8m,此时应将梯子再向墙推进多少米?
参考答案
1.【解答】解:在直角△ABC′中,BC′是斜边,
已知AB=1.5m,BC′=BC=AC﹣AB=3.9m,
则根据勾股定理AC′==3.6m,
3.6<4,所以电线杆不会落在离它的底部4m的快车道上.
答:电线杆顶部不会落在离它的底部4m的快车道上.
2.【解答】解:设BB′与矩形的宽的交点为C,
∵AB=1,AC=0.8,∠ACB=90°,
∴BC===0.6米,
∵BB′=BC+CB′=2.3+0.6=2.9<3.0,
∴不能通过.
3.【解答】解:①将正面和左面展开,过点B向底面作垂线,垂足为点C,则△ABC为直角三角形,
∵AC=×8+×6=8m,BC=5m,
∴AB===m.
故壁虎爬到蚊子处的最短距离为m.
②将正面和上面展开,则A到B的水平距离为6m,垂直距离为7m,
此时的最短距离为m
③将下面和右面展开,则A到B的水平距离为11m,垂直距离为2m,
此时的最短距离为5m.
综上所述,壁虎爬到蚊子处的最短距离为米.
4.【解答】解:∵BC==2.4,
∴当一直角边为BC﹣0.4=2,斜边为2.5时,另一直角边为=1.5.
故梯子的底部向外滑出1.5﹣0.7=0.8(米).
5.【解答】解:=20.
故湖泊的宽度为20m.
6.【解答】解:根据图中所标数据求得:AC=40﹣21=19mm,BC=60﹣21=39mm,
∴AB=≈43.4mm.
7.【解答】解:(1)是.理由如下:
在△CHB中,CB=2.5,CH=2,HB=1.5,
∵CH2+HB2=22+1.52=6.25,CB2=2.52=6.25,
∴CH2+HB2=CB2,
∴CH⊥AB,
故CH是从村庄C到河边的最近路;
(2)设AC=x千米,则AB=AC=x千米,AH=x﹣1.5(千米)
在Rt△AHC中,由勾股定理得:AH2+HC2=AC2
∴x2=(x﹣1.5)2+22
解得:x≈2.08
答:原来的路线AC的长约为2.08千米.
8.【解答】解:∵BC=1m,NC= m,BN=m,
∴BC2=1,NC2=,BN2=,
∴BC2+NC2=BN2,
∴AC⊥MC.
在Rt△ACM中,
∵AC=4.5m,MC=6m,MA2=AC2+CM2=56.25,
∴MA=7.5 m.
9.【解答】解:∵一轮船以16n mi1e/h的速度从港口A出发向东北方向航行,
另一轮船以12n mi1e/h的速度同时从港口出发向东南方向航行,
∴∠BAC=90°,离开港口A2h后,AB=32n mi1e,AC=24n mi1e,
∴BC==40(n mi1e).
答:离开港口A2h后,两船相距40n mi1e.
10.【解答】解:(1)大棚的占地面积为:ad=4.8×10=48(m2);
(2)根据勾股定理,得直角三角形的斜边为=6(m),
由矩形的面积公式,得覆盖在顶上的塑料布为:6×10=60(m2).
11.【解答】解:图(1)中,管道长为2a;
图(2)中,AD===a,
则管道长为a+a;
图(3)中,设OE=x,则OB为2x,
由勾股定理得(2x)2﹣x2=(a)2,
解得:x=a,
则OB=a,管道长为a×3=a,
∵2a>a+a>a,
∴图(3)的辅助设方案最好.
12.【解答】解:将台阶展开,如下图,
因为AC=3×3+1×3=12,BC=5,
所以AB2=AC2+BC2=169,
所以AB=13(cm),
所以蚂蚁爬行的最短线路为13cm.
答:蚂蚁爬行的最短线路为13cm.
13.【解答】解:(1)∵50<100,
∴学校会受到拖拉机的影响;
(2)如图:作AC⊥MN于C,则AC=50.
假设当拖拉机行驶到B点开始影响学校,行驶到D点结束对学校的影响,
则AB=AD=100米,
∴BC=CD==50米,
∴BD=2×50=100米,
∵18千米/时=5米/秒
所以影响学校的时间为:100÷5=20秒
∴拖拉机会影响学校,影响时间为20秒.
14.【解答】解:我的意见是直角三角形.
∵32+42=25,52=25,
∴32+42=52
∴以3、4、5为边长的三角形是直角三角形.
15.【解答】解:连接AC.
由勾股定理可知:AC===5,
又∵AC2+BC2=52+122=132=AB2,
∴△ABC是直角三角形,
∴这块地的面积=△ABC的面积﹣△ACD的面积=×5×12﹣×3×4=24(米2).
16.【解答】解:(1)在Rt△AOB中,OA=100,∠BAO=60°,
∴OB=OAtan∠BAO=100.
Rt△AOC中,
∵∠CAO=45°,
∴OC=OA=100.
∴B(﹣100,0),C(100,0).
(2)∵BC=BO+OC=100+100,
∴≈18>,
∴汽车在这段限速路上超速了.
17.【解答】解:(1)由题意得:EF=5m,CF=4m,
则EC===3(m).
答:梯子的顶端距地面的垂直距离是3m;
(2)由题意得:BF=1m,则CB=4﹣1=3(m),
AC===4(m),
则AE=AC﹣EC=1m.
答:梯子的顶端升高了1m;
(3)若AC=4.8m,则BC===1.4(m),
应将梯子再向墙推进3﹣1.4=1.6(m).
答:应将梯子再向墙推进1.6m.
