人教版六年级下册4.3.3《用比例解决问题(例5)》课件(23张ppt)
文档属性
| 名称 | 人教版六年级下册4.3.3《用比例解决问题(例5)》课件(23张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-31 20:21:25 | ||
图片预览






文档简介
(共23张PPT)
用比例解决问题(例5)
数学人教版 六年级下
学习目标
1.能够正确判断情境中的两个相关联的量是否成正比例关系,并能利用正比例的意义解决实际问题。
2.学会从不同角度思考问题,沟通“算术法”与“比例法”的联系和区别。
3.发展分析问题、解决问题的能力。
1.比例的意义?
2.什么是正比例?
3.什么是反比例?
表示两个比相等的式子
如果两种相关联的量的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
如果两种相关联的量的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
乘积一定反比例,比值一定正比例,其它一定不成比例
1.总价一定,单价和数量
单价×数量=总价(一定),总价一定,单价和数量成反比例。
2.速度一定,路程和时间
3.总钱数一定,用去的钱数和剩下的钱数
=速度(一定),速度一定,
路程和时间成正比例。
时间
路程
用去的钱数+剩下的钱数=总钱数(一定),这两种量不成比例。
能组成比例 成反比例。
能组成比例 成正比例。
不成比例。
判断下面各题中两种相关联的量能否组成比例?成什么比例?
张大妈
李奶奶
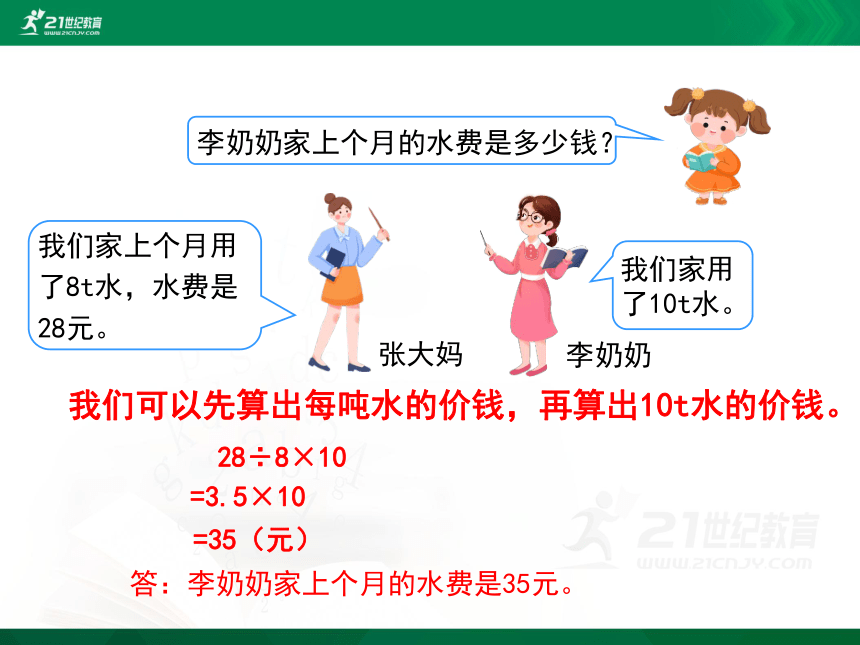
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
用水量
总价
用水量
要解决水费问题,就要知道水的单价和用水量。
水的单价虽然不知道,但它是一定的。
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
我们可以先算出每吨水的价钱,再算出10t水的价钱。
28÷8×10
=3.5×10
=35(元)
答:李奶奶家上个月的水费是35元。
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
我们还可以先算出用水量的倍数关系,再求总价。
28×(10÷8)
=28×1.25
=35(元)
答:李奶奶家上个月的水费是35元。
10t=1.25个8t
每8t水的价格是28元
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
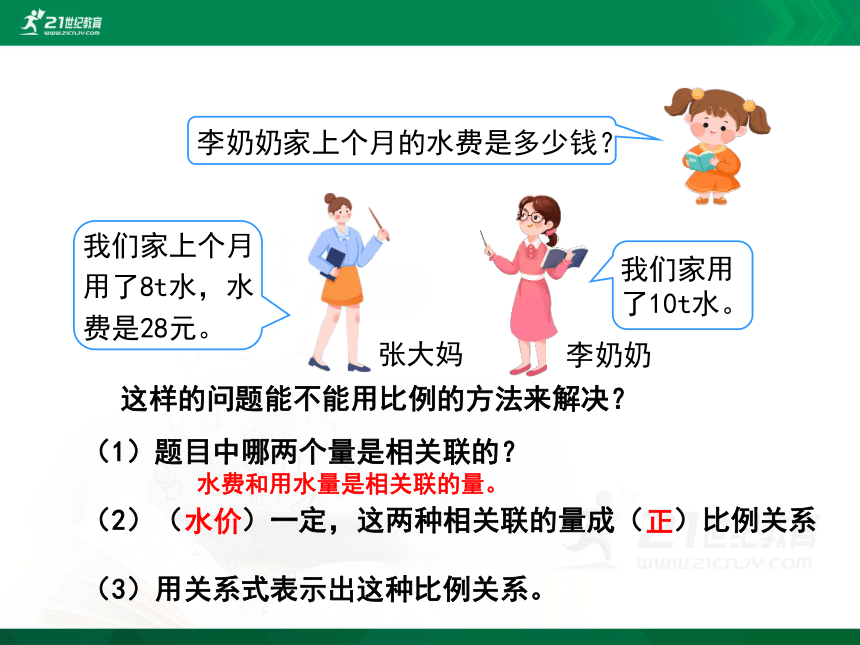
这样的问题能不能用比例的方法来解决?
(1)题目中哪两个量是相关联的?
(2)( )一定,这两种相关联的量成( )比例关系
(3)用关系式表示出这种比例关系。
水费和用水量是相关联的量。
水价
正
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
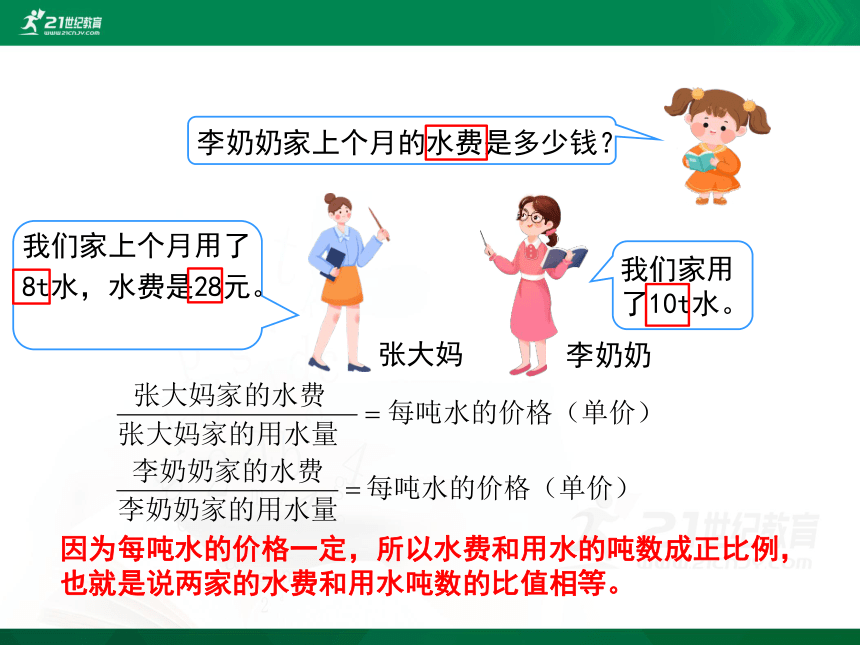
因为每吨水的价格一定,所以水费和用水的吨数成正比例,也就是说两家的水费和用水吨数的比值相等。
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
解:设李奶奶家上个月的水费是x元。
答:李奶奶家上个月的水费是35元。
35×8=280
28×10=280
检 验:
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
答:李奶奶家上个月的水费是35元。
一定
检 验:
35×8=280
28×10=280
解:设李奶奶家上个月的水费是 元。
8:10=28:
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
解:设李奶奶家上个月的水费是 元。
答:李奶奶家上个月的水费是35元。
解决这个问题的关键是找到不变的量。
只要两个量的比值一定,就可以用正比例关系解答。
=
=
28×10
=35
28÷8×10
=3.5×10
=35(元)
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
解:设李奶奶家上个月的水费是x元。
8
28
=
10
x
8x=28×10
x=
28×10
8
x=35
答:李奶奶家上个月的水费是35元。
算术法:
比例法:
“算术法”和“比例法”解题时有什么联系和区别
王大爷家上个月的水费是42元,
上个月用了多少吨水?
解:设王大爷家上个月用了x吨水。
x = 12
答:王大爷家上个月用了12吨水。
x =
8×42
28
28x=8×42
=
8
28
x
42
我们家上个月用了8t水,水费是28元。
张大妈
单价一定
用比例的方法解决
检 验:
28×12=336
8×42=336
用正比例知识解决问题的方法:
(2)判断比例关系,在正比例关系中,两个相关联量的比值一定。
(3)根据这个意义,来列比例式。
(4)最后把这个比例式解出来,并检验。
(1)找一定的量。
1.找 2.判 3.列 4.解
1. 小明买4支圆珠笔用了6元,小刚想买3支同样的圆珠
笔,要用多少钱?
解:设要用x元。
4x=3×6
x=4.5
答:要用4.5元。
=
4
6
3
x
学以致用:
数量
总价
单价一定
检 验:
4×4.5=18
6×3=18
总价÷数量=单价
x=
学以致用:
2.小明的身高是1.5米,他的影长是2.4米。如果同一时间、同一地点测得一棵树的影子长4m,这棵树实际高几米?(用比例解答)
实际高度与影长的比值一定
解:设这棵树实际高 米。
答:这棵树实际高2.5米。
检 验:
学以致用:
3.一根木料锯成3段需要9分钟,照这样计算,锯成6段需要多少分钟?(用比例解答)
锯成3段要锯2次,9分钟对应2次的时间。
问题求的是锯5 次的时间。
每锯一次的时间一定。
解:设锯成6段需要 分钟。
答:锯成6段需要22.5分钟。
检 验:
段数,不是次数。
学以致用:
4.客车和货车同时从A、B两地相对开出,它们的速度之比是6:5,相遇时客车行驶了75Km,货车行驶了多少千米?
相遇问题
两车同时启动,
相遇时同时停止。
它们所行的时间一定。
解:设货车行驶了 千米。
答:货车行驶了62.5千米。
检 验:
宝剑锋从磨砺出,梅花香自苦寒来。
---陆游
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
用比例解决问题(例5)
数学人教版 六年级下
学习目标
1.能够正确判断情境中的两个相关联的量是否成正比例关系,并能利用正比例的意义解决实际问题。
2.学会从不同角度思考问题,沟通“算术法”与“比例法”的联系和区别。
3.发展分析问题、解决问题的能力。
1.比例的意义?
2.什么是正比例?
3.什么是反比例?
表示两个比相等的式子
如果两种相关联的量的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
如果两种相关联的量的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
乘积一定反比例,比值一定正比例,其它一定不成比例
1.总价一定,单价和数量
单价×数量=总价(一定),总价一定,单价和数量成反比例。
2.速度一定,路程和时间
3.总钱数一定,用去的钱数和剩下的钱数
=速度(一定),速度一定,
路程和时间成正比例。
时间
路程
用去的钱数+剩下的钱数=总钱数(一定),这两种量不成比例。
能组成比例 成反比例。
能组成比例 成正比例。
不成比例。
判断下面各题中两种相关联的量能否组成比例?成什么比例?
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
用水量
总价
用水量
要解决水费问题,就要知道水的单价和用水量。
水的单价虽然不知道,但它是一定的。
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
我们可以先算出每吨水的价钱,再算出10t水的价钱。
28÷8×10
=3.5×10
=35(元)
答:李奶奶家上个月的水费是35元。
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
我们还可以先算出用水量的倍数关系,再求总价。
28×(10÷8)
=28×1.25
=35(元)
答:李奶奶家上个月的水费是35元。
10t=1.25个8t
每8t水的价格是28元
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
这样的问题能不能用比例的方法来解决?
(1)题目中哪两个量是相关联的?
(2)( )一定,这两种相关联的量成( )比例关系
(3)用关系式表示出这种比例关系。
水费和用水量是相关联的量。
水价
正
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
因为每吨水的价格一定,所以水费和用水的吨数成正比例,也就是说两家的水费和用水吨数的比值相等。
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
解:设李奶奶家上个月的水费是x元。
答:李奶奶家上个月的水费是35元。
35×8=280
28×10=280
检 验:
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
答:李奶奶家上个月的水费是35元。
一定
检 验:
35×8=280
28×10=280
解:设李奶奶家上个月的水费是 元。
8:10=28:
张大妈
李奶奶
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
解:设李奶奶家上个月的水费是 元。
答:李奶奶家上个月的水费是35元。
解决这个问题的关键是找到不变的量。
只要两个量的比值一定,就可以用正比例关系解答。
=
=
28×10
=35
28÷8×10
=3.5×10
=35(元)
我们家上个月用了8t水,水费是28元。
我们家用了10t水。
李奶奶家上个月的水费是多少钱?
解:设李奶奶家上个月的水费是x元。
8
28
=
10
x
8x=28×10
x=
28×10
8
x=35
答:李奶奶家上个月的水费是35元。
算术法:
比例法:
“算术法”和“比例法”解题时有什么联系和区别
王大爷家上个月的水费是42元,
上个月用了多少吨水?
解:设王大爷家上个月用了x吨水。
x = 12
答:王大爷家上个月用了12吨水。
x =
8×42
28
28x=8×42
=
8
28
x
42
我们家上个月用了8t水,水费是28元。
张大妈
单价一定
用比例的方法解决
检 验:
28×12=336
8×42=336
用正比例知识解决问题的方法:
(2)判断比例关系,在正比例关系中,两个相关联量的比值一定。
(3)根据这个意义,来列比例式。
(4)最后把这个比例式解出来,并检验。
(1)找一定的量。
1.找 2.判 3.列 4.解
1. 小明买4支圆珠笔用了6元,小刚想买3支同样的圆珠
笔,要用多少钱?
解:设要用x元。
4x=3×6
x=4.5
答:要用4.5元。
=
4
6
3
x
学以致用:
数量
总价
单价一定
检 验:
4×4.5=18
6×3=18
总价÷数量=单价
x=
学以致用:
2.小明的身高是1.5米,他的影长是2.4米。如果同一时间、同一地点测得一棵树的影子长4m,这棵树实际高几米?(用比例解答)
实际高度与影长的比值一定
解:设这棵树实际高 米。
答:这棵树实际高2.5米。
检 验:
学以致用:
3.一根木料锯成3段需要9分钟,照这样计算,锯成6段需要多少分钟?(用比例解答)
锯成3段要锯2次,9分钟对应2次的时间。
问题求的是锯5 次的时间。
每锯一次的时间一定。
解:设锯成6段需要 分钟。
答:锯成6段需要22.5分钟。
检 验:
段数,不是次数。
学以致用:
4.客车和货车同时从A、B两地相对开出,它们的速度之比是6:5,相遇时客车行驶了75Km,货车行驶了多少千米?
相遇问题
两车同时启动,
相遇时同时停止。
它们所行的时间一定。
解:设货车行驶了 千米。
答:货车行驶了62.5千米。
检 验:
宝剑锋从磨砺出,梅花香自苦寒来。
---陆游
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
