人教版数学八年级下册18.2正方形同步练习(解析版)
文档属性
| 名称 | 人教版数学八年级下册18.2正方形同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 253.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-31 20:33:49 | ||
图片预览


文档简介
人教版数学八年级18.2正方形测试题
一.选择题(每题3分,共30分)
1.在四边形ABCD中,AC、BD相交于O点,下列条件能判断四边形ABCD是正方形的是()
A.OA=OC,OB=OC
B.OA=OB=OC=OD
C.OA=OC,OB=OD,AC=BD
D.OA=OB=OC=OD,AC⊥BD
2.已知四边形ABCD中,∠A=∠B=∠C=90°.如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是()
A.∠D=90°
B.AB=CD
C.AD=BC
D.BC=CD
3.如图,在正方形ABCD中,E为对角线AC上一点,连接EB、ED,延长BE交AD于点F,若∠DEB=140°,则∠AFE的度数为()
A.65°
B.70°
C.60°
D.80°
4.菱形、矩形、正方形都具有的性质是()
A.对角线相等且互相平分
B.对角线相等且互相垂直平分
C.对角线互相平分
D.四条边相等,四个角相等
5.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为()
A.5 B.2 C.7 D.29
6.点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为()
A.5
B.23
C.7
D.29
7.如图,在正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰直角三角形有()
A.4个
B.6个
C.8个
D.10个
8.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E、F两点,下列说法正确的是( )
A.若AD⊥BC,则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
9.下列命题中,正确的是()
A.四条边相等的四边形是正方形
B.四个角相等的四边形是正方形
C.对角线互相垂直的平行四边形是正方形
D.对角线相等的菱形是正方形
10.如图,在△ABC中,点D,E分别是边AB,AC的中点,将△ADE绕点E旋转180°得△CFE,连接AF,CD,添加下列条件后能判定四边形ADCF是正方形的是( )
A.AC=BC B.∠ACB=90°
C.AC=BC且∠B=45° D.AC=BC且∠B=60°
二.填空题(每题3分,共24分)
11.如图,正方形ABCD,△ABE是等边三角形,则∠AED=?? ??.
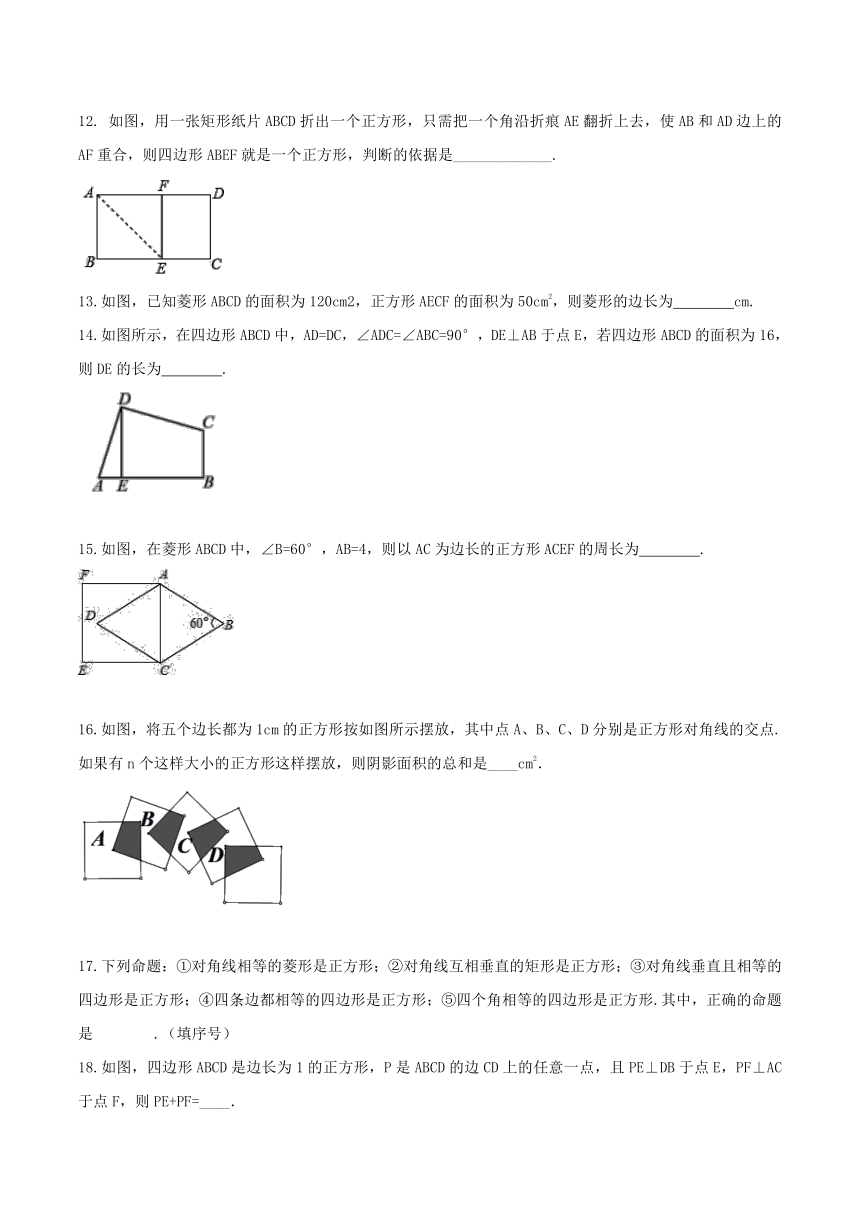
12. 如图,用一张矩形纸片ABCD折出一个正方形,只需把一个角沿折痕AE翻折上去,使AB和AD边上的AF重合,则四边形ABEF就是一个正方形,判断的依据是_____________.
13.如图,已知菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为????cm.
14.如图所示,在四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB于点E,若四边形ABCD的面积为16,则DE的长为????.
15.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为????.
16.如图,将五个边长都为1cm的正方形按如图所示摆放,其中点A、B、C、D分别是正方形对角线的交点.如果有n个这样大小的正方形这样摆放,则阴影面积的总和是____cm2.
17.下列命题:①对角线相等的菱形是正方形;②对角线互相垂直的矩形是正方形;③对角线垂直且相等的四边形是正方形;④四条边都相等的四边形是正方形;⑤四个角相等的四边形是正方形.其中,正确的命题是????.(填序号)
18.如图,四边形ABCD是边长为1的正方形,P是ABCD的边CD上的任意一点,且PE⊥DB于点E,PF⊥AC于点F,则PE+PF=____.
三.解答题(共66分)
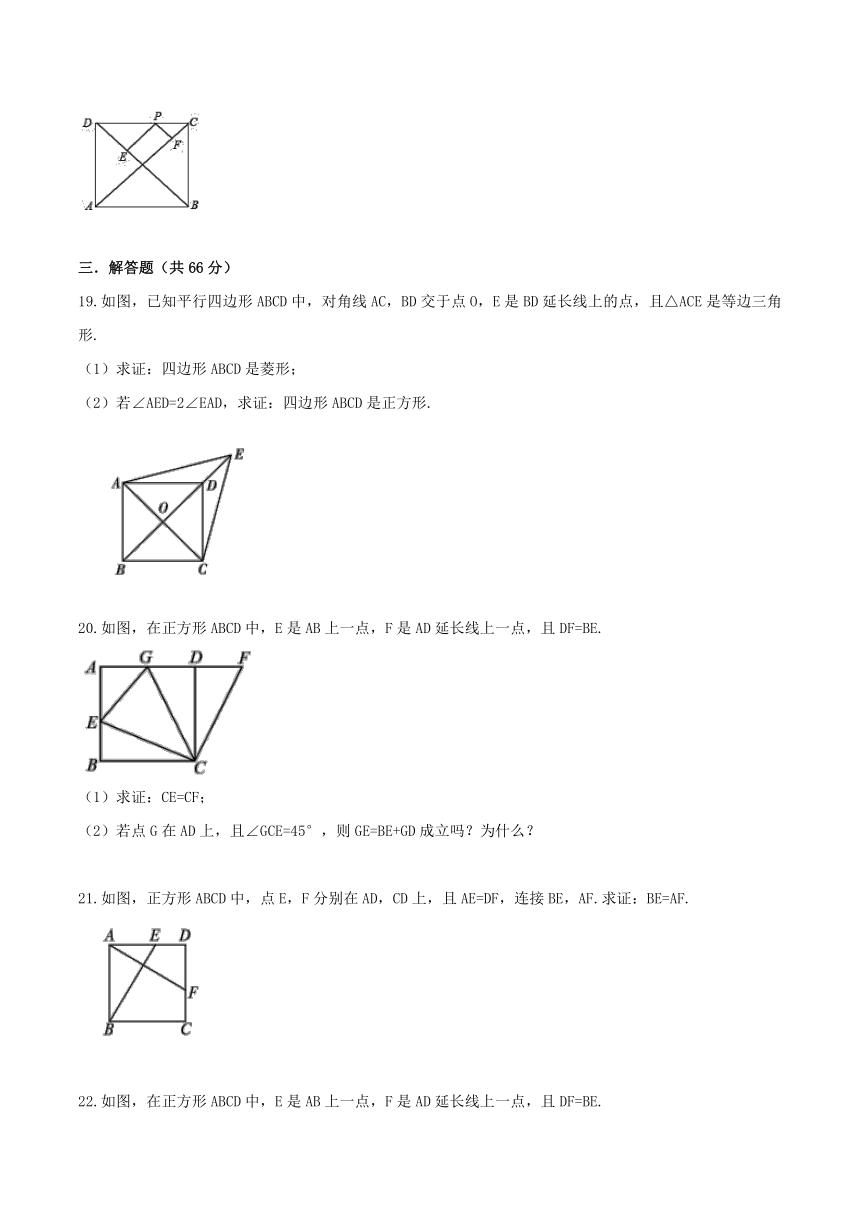
19.如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
20.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
21.如图,正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF.
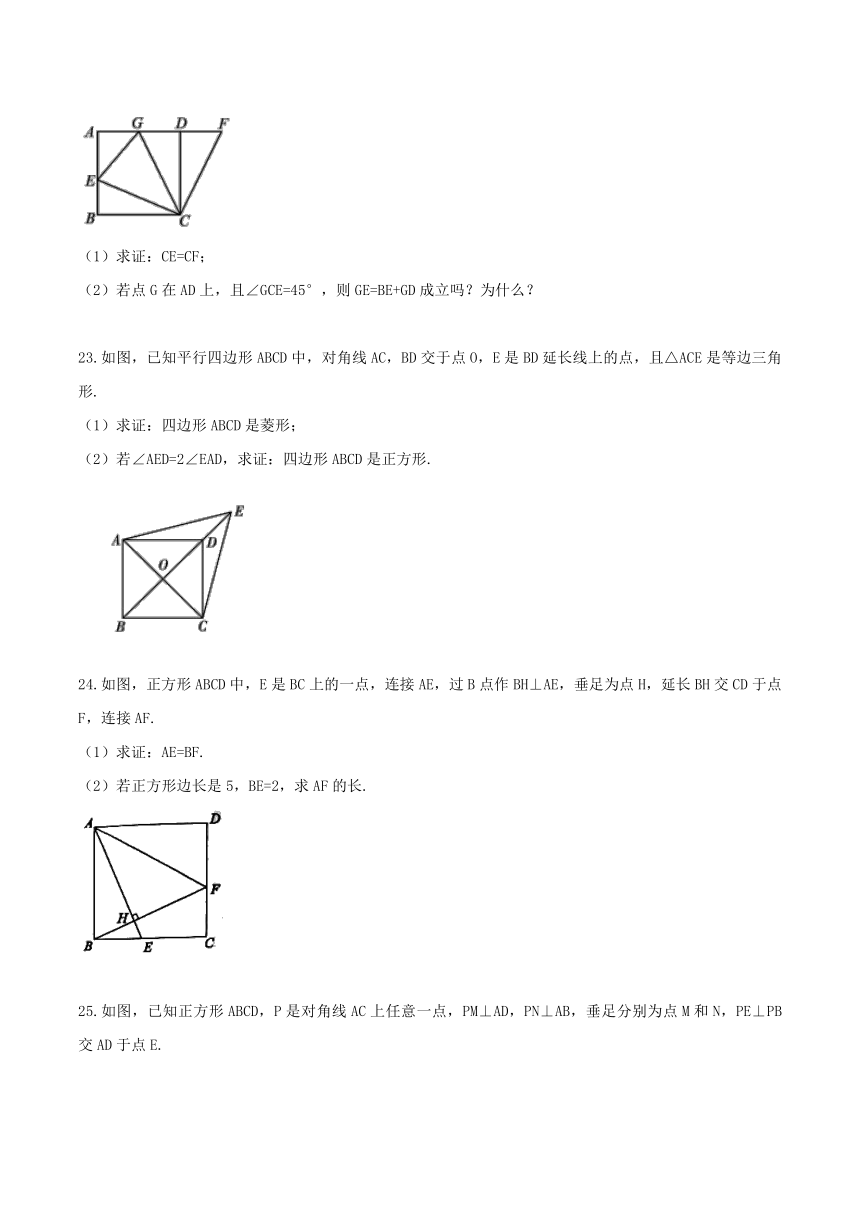
22.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
23.如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
24.如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证:AE=BF.
(2)若正方形边长是5,BE=2,求AF的长.
25.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.
(1)求证:四边形MANP是正方形;
(2)求证:EM=BN.
人教版数学八年级18.2正方形测试题答案
一.选择题(每题3分,共30分)
1.答案:D.
解:根据对角线垂直平分且相等的四边形是正方形知:D正确.
故选D.
2.答案:D.
解:∵四边形ABCD中,∠A=∠B=∠C=90°,
∴四边形ABCD是矩形,
当一组邻边相等时,矩形ABCD为正方形,
这个条件可以是:BC=CD.
故选D.
3.答案:A.
解:∵四边形ABCD是正方形,
∴CD=CB,∠DCA=∠BCA.
又∵CE=CE,
∴△DEC≌△BEC.
∴∠DEC=∠BEC.
∵∠DEB=140°,
∴∠DEC=∠BEC=70°.
∴∠AEF=∠BEC=70°.
∵∠DAB=90°,
∴∠DAC=∠BAC=45°,
∴∠AFE=180°-70°-45°=65°.
故选A.
4.答案:C.
解:选项A是矩形和正方形都有的性质,而菱形不具有,故选项A错误;
选项B是正方形所具有的性质,而矩形和菱形不具有,故选项B错误;
选项C是矩形、菱形和正方形都具有的性质,故选项C正确;
选项D是正方形所具有的性质,而菱形和矩形不具有,故选项D错误.
故选C.
5.如图所示,在菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为()
A.14
B.15
C.16
D.17
答案:D.
解:
∵把△ADE绕点A顺时针旋转90°到△ABF的位置,
∴△ADE≌△ABF,
∴四边形AECF的面积等于正方形ABCD的面积为25,
∴AD=5.
∵AD=5,DE=2,∠ADE=90°,
∴AE=29.
故选D.
7.
答案:C.
解:∵正方形ABCD中,对角线AC,BD相交于点O,
∴AB=BC=CD=AD,AO=OD=OC=OB,AC⊥BD,
∴△ABC,△BCD,△ADC,△ABD,△AOB,△BOC,△COD,△AOD都是等腰直角三角形,一共8个.
故选C.
8.
答案:D.
解:∵AC∥DE,AB∥DF,
∴四边形AEDF是平行四边形.
要使平行四边形AEDF是矩形,则有一个角是直角即可,而AD⊥BC和AD垂直平分BC,并不能证明出直角的存在,
若要使平行四边形AEDF是菱形,则对角线平分对角即可,故可添加AD平分∠BAC,而BD=CD不能证明平行四边形AEDF是菱形.
故选D
9.答案:D.
解:四边相等的四边形也可能是菱形,不一定是正方形,故A命题不正确;
四角相等的四边形也可能是矩形,不一定是正方形,故命题B不正确;
对角线垂直且相等的四边形可能是正方形,也可能是等腰梯形,故C命题不正确;
对角线相等的菱形是正方形,符合正方形的判定,正确.
故选D.
10.答案:C.
解:∵AC=BC,点D,E分别是边AB,AC的中点,
∴DE=12BC,AE=12AC,
∵AC=BC,
∴AE=DE,
∵将△ADE绕点E旋转180°得△CFE,
∴△ADE≌△CFE,
∴四边形ADCF是平行四边形,
∵AE=CE,DE=EF,AE=DE,
∴AE=CE=DE=EF,
∴AC=DF,
∴四边形ADCF是矩形,
∴添加AD=DC即可使矩形ADCF是正方形,
∴当AC=BC且∠B=45°时AD=DC.
故选C.
填空题(每题3分,共24分)
11.答案:75°.
解:∵四边形ABCD是正方形,
∴AB=AD,∠DAB=90°.
∵△ABE为等边三角形,
∴AE=AB,∠EAB=60°,
∴AE=AD,∠DAE=90°-60°=30°,
∴∠AED=∠ADE=12(180°-30°)=75°.
12.答案:邻边相等的矩形是正方形.
解:∵四边形ABCD是矩形,
∴∠B=∠DAB=90°,
∵沿折痕AE翻折上去,使AB和AD边上的AF重合,
∴∠AFE=∠B=90°,AB=AF,
∵∠AFE=∠B=∠DAB=90°
∴四边形ABEF是矩形,
又∵AB=AF,
∴矩形ABEF是正方形.
13.答案:13.
解:连接AC和BD,相交于点O,如下图,
∵正方形AECF的面积为50cm2,
∴正方形AECF的边长AF=50=52(cm),
∴AC=2AF2=10(cm),
∴OA=5cm.
∵菱形的面积为ABCD的面积为120cm2,
∴12AC?BD=120,
即10BD=240,
∴BD=24(cm),
∴OB=12cm,
∴AB=OA2+OB2=52+122=13(cm),
即菱形ABCD的边长为13cm.
14.答案:4.
解:过点D作BC的垂线,交BC的延长线于点F.
∵∠ADC=∠ABC=90°,
∴∠A+∠BCD=180°.
∵∠FCD+∠BCD=180°,
∴∠A=∠FCD.
又∵∠AED=∠F=90°,AD=DC,
∴△ADE≌△CDF,
∴DE=DF.
∴四边形DEBF是正方形,S正方形DEBF=S四边形ABCD=16,
∴DE=4.
15.答案:16.
解:∵四边形ABCD是菱形,AB=4,
∴AB=BC=4.
∵∠B=60°,
∴△ABC等边三角形,
∴AC=AB=BC=4.
∵四边形ACEF是正方形,
∴AC=CE=EF=FA=4,
∴正方形ACEF的周长为4×4=16.
16.答案:n?1/4.
解:∵点A、B、C、D分别是正方形对角线的交点,
∴两个正方形之间的阴影面积为正方形总面积的1/4,
即1/4×1×1=14,
当有三个正方形时,其面积为1/4+1/4=2/4,
当有四个时,其面积为1/4+1/4+1/4=34,
所以当n个正方形时,其面积为n?1/4.
故答案为n?1/4.
17.答案:①②.
解:①②正确;
③应为“对角线垂直且相等的四边形可能是正方形,也可能是等腰梯形”,故③错误;
④应为“四条边都相等的四边形是菱形”,故④错误;
⑤中四个角都相等的四边形可能是矩形,也可能是正方形,故⑤错误.
18.答案.
解:∵ABCD是正方形,
∴OA=OD,AO⊥BD.
连接OP,易得S△AOD=S△AOP=S△ODP,即1/2OA·PE+1/2OD·PF=1/2OD·AO,
∴PE+PF=AE.
在Rt△ABD中,根据勾股定理就易得BD=
根据△ABD的面积=1/2AB·AD=1/2BD·AE,
解得AE=,则PE+PF=.
解答题(共66分)
19.证明:(1)∵四边形ABCD是平行四边形,
∴AO=CO.
∵△ACE是等边三角形,
∴EO⊥AC,即AC⊥BD,
∴四边形ABCD是菱形.
(2)∵四边形ABCD是平行四边形,
∴AO=CO.
∵△ACE是等边三角形,
∴EO平分∠AEC,
∴∠AED=1/2∠AEC=1/2×60°=30°.
∵∠AED=2∠EAD,
∴∠EAD=15°,
∴∠ADO=∠DAE+∠DEA=15°+30°=45°.
∵四边形ABCD是菱形,
∴∠ADC=2∠ADO=90°,
∴平行四边形ABCD是正方形.
20.解:(1)证明:
∵四边形ABCD是正方形
∴BC=DC,∠ABC=∠CDF=90°
∵BC=DC,∠CBE=∠CDF,BE=DF
∴△CBE≌△CDF
∴CE=CF;
(2)解:GE=BE+GD成立.理由是:
∵△CBE≌△CDF
∴∠BCE=∠DCF
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°
∵∠GCE=45°
∴∠GCF=∠GCE=45°
∵CE=CF,∠GCE=∠GCF,GC=GC
∴△ECG≌△FCG
∴GE=GF
∴GE=DF+GD=BE+GD.
21.证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠EAB=90°.
在△EAB和△FDA中,AF=DF,∠EAB=∠D,AB=AD,
∴△EAB≌△FDA,
∴BE=AF.
22.解:(1)证明:
∵四边形ABCD是正方形
∴BC=DC,∠ABC=∠CDF=90°
∵BC=DC,∠CBE=∠CDF,BE=DF
∴△CBE≌△CDF
∴CE=CF;
(2)解:GE=BE+GD成立.理由是:
∵△CBE≌△CDF
∴∠BCE=∠DCF
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°
∵∠GCE=45°
∴∠GCF=∠GCE=45°
∵CE=CF,∠GCE=∠GCF,GC=GC
∴△ECG≌△FCG
∴GE=GF
∴GE=DF+GD=BE+GD.
23.证明:(1)∵四边形ABCD是平行四边形,
∴AO=CO.
∵△ACE是等边三角形,
∴EO⊥AC,即AC⊥BD,
∴四边形ABCD是菱形.
(2)∵四边形ABCD是平行四边形,
∴AO=CO.
∵△ACE是等边三角形,
∴EO平分∠AEC,
∴∠AED=12∠AEC=12×60°=30°.
∵∠AED=2∠EAD,
∴∠EAD=15°,
∴∠ADO=∠DAE+∠DEA=15°+30°=45°.
∵四边形ABCD是菱形,
∴∠ADC=2∠ADO=90°,
∴平行四边形ABCD是正方形.
24.解:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°.
∵BH⊥AE,∠ABC=90°,
∴∠HBA+∠BAH=90°,∠ABH+∠CBF=90°,
∴∠EAB=∠FBC,
∴△ABE≌△BCF,
∴AE=BF.
(2)
∵△ABE≌△BCF,
∴BE=CF.
∵正方形的边长为5,BE=CF=2,
∴AD=CD=5,∠D=90°
∴DF=3,
∴AF=
25.
(1)证明:
∵四边形ABCD是正方形,
∴∠NAM=90°.
又∵PM⊥AD,PN⊥AB,
∴∠ANP=∠AMP=90°,
∴四边形PMAN是矩形.
∵P在AC上,
∴PM=PN,
∴四边形PMAN是正方形.
(2)
∵四边形PMAN是正方形,
∴∠MPN=∠MPE+∠EPN=90°.
∵PE⊥PB,
∴∠BPN+∠EPN=90°.
∴∠BPN=∠EPM.
在△BPN与△EPM中,
∵∠BPN=∠EPM,PN=PM,∠BNP=∠EMP=90°,
∴△BPN≌△EPM,
∴BN=EM.
一.选择题(每题3分,共30分)
1.在四边形ABCD中,AC、BD相交于O点,下列条件能判断四边形ABCD是正方形的是()
A.OA=OC,OB=OC
B.OA=OB=OC=OD
C.OA=OC,OB=OD,AC=BD
D.OA=OB=OC=OD,AC⊥BD
2.已知四边形ABCD中,∠A=∠B=∠C=90°.如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是()
A.∠D=90°
B.AB=CD
C.AD=BC
D.BC=CD
3.如图,在正方形ABCD中,E为对角线AC上一点,连接EB、ED,延长BE交AD于点F,若∠DEB=140°,则∠AFE的度数为()
A.65°
B.70°
C.60°
D.80°
4.菱形、矩形、正方形都具有的性质是()
A.对角线相等且互相平分
B.对角线相等且互相垂直平分
C.对角线互相平分
D.四条边相等,四个角相等
5.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为()
A.5 B.2 C.7 D.29
6.点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为()
A.5
B.23
C.7
D.29
7.如图,在正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰直角三角形有()
A.4个
B.6个
C.8个
D.10个
8.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E、F两点,下列说法正确的是( )
A.若AD⊥BC,则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
9.下列命题中,正确的是()
A.四条边相等的四边形是正方形
B.四个角相等的四边形是正方形
C.对角线互相垂直的平行四边形是正方形
D.对角线相等的菱形是正方形
10.如图,在△ABC中,点D,E分别是边AB,AC的中点,将△ADE绕点E旋转180°得△CFE,连接AF,CD,添加下列条件后能判定四边形ADCF是正方形的是( )
A.AC=BC B.∠ACB=90°
C.AC=BC且∠B=45° D.AC=BC且∠B=60°
二.填空题(每题3分,共24分)
11.如图,正方形ABCD,△ABE是等边三角形,则∠AED=?? ??.
12. 如图,用一张矩形纸片ABCD折出一个正方形,只需把一个角沿折痕AE翻折上去,使AB和AD边上的AF重合,则四边形ABEF就是一个正方形,判断的依据是_____________.
13.如图,已知菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为????cm.
14.如图所示,在四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB于点E,若四边形ABCD的面积为16,则DE的长为????.
15.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为????.
16.如图,将五个边长都为1cm的正方形按如图所示摆放,其中点A、B、C、D分别是正方形对角线的交点.如果有n个这样大小的正方形这样摆放,则阴影面积的总和是____cm2.
17.下列命题:①对角线相等的菱形是正方形;②对角线互相垂直的矩形是正方形;③对角线垂直且相等的四边形是正方形;④四条边都相等的四边形是正方形;⑤四个角相等的四边形是正方形.其中,正确的命题是????.(填序号)
18.如图,四边形ABCD是边长为1的正方形,P是ABCD的边CD上的任意一点,且PE⊥DB于点E,PF⊥AC于点F,则PE+PF=____.
三.解答题(共66分)
19.如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
20.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
21.如图,正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF.
22.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
23.如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
24.如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证:AE=BF.
(2)若正方形边长是5,BE=2,求AF的长.
25.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.
(1)求证:四边形MANP是正方形;
(2)求证:EM=BN.
人教版数学八年级18.2正方形测试题答案
一.选择题(每题3分,共30分)
1.答案:D.
解:根据对角线垂直平分且相等的四边形是正方形知:D正确.
故选D.
2.答案:D.
解:∵四边形ABCD中,∠A=∠B=∠C=90°,
∴四边形ABCD是矩形,
当一组邻边相等时,矩形ABCD为正方形,
这个条件可以是:BC=CD.
故选D.
3.答案:A.
解:∵四边形ABCD是正方形,
∴CD=CB,∠DCA=∠BCA.
又∵CE=CE,
∴△DEC≌△BEC.
∴∠DEC=∠BEC.
∵∠DEB=140°,
∴∠DEC=∠BEC=70°.
∴∠AEF=∠BEC=70°.
∵∠DAB=90°,
∴∠DAC=∠BAC=45°,
∴∠AFE=180°-70°-45°=65°.
故选A.
4.答案:C.
解:选项A是矩形和正方形都有的性质,而菱形不具有,故选项A错误;
选项B是正方形所具有的性质,而矩形和菱形不具有,故选项B错误;
选项C是矩形、菱形和正方形都具有的性质,故选项C正确;
选项D是正方形所具有的性质,而菱形和矩形不具有,故选项D错误.
故选C.
5.如图所示,在菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为()
A.14
B.15
C.16
D.17
答案:D.
解:
∵把△ADE绕点A顺时针旋转90°到△ABF的位置,
∴△ADE≌△ABF,
∴四边形AECF的面积等于正方形ABCD的面积为25,
∴AD=5.
∵AD=5,DE=2,∠ADE=90°,
∴AE=29.
故选D.
7.
答案:C.
解:∵正方形ABCD中,对角线AC,BD相交于点O,
∴AB=BC=CD=AD,AO=OD=OC=OB,AC⊥BD,
∴△ABC,△BCD,△ADC,△ABD,△AOB,△BOC,△COD,△AOD都是等腰直角三角形,一共8个.
故选C.
8.
答案:D.
解:∵AC∥DE,AB∥DF,
∴四边形AEDF是平行四边形.
要使平行四边形AEDF是矩形,则有一个角是直角即可,而AD⊥BC和AD垂直平分BC,并不能证明出直角的存在,
若要使平行四边形AEDF是菱形,则对角线平分对角即可,故可添加AD平分∠BAC,而BD=CD不能证明平行四边形AEDF是菱形.
故选D
9.答案:D.
解:四边相等的四边形也可能是菱形,不一定是正方形,故A命题不正确;
四角相等的四边形也可能是矩形,不一定是正方形,故命题B不正确;
对角线垂直且相等的四边形可能是正方形,也可能是等腰梯形,故C命题不正确;
对角线相等的菱形是正方形,符合正方形的判定,正确.
故选D.
10.答案:C.
解:∵AC=BC,点D,E分别是边AB,AC的中点,
∴DE=12BC,AE=12AC,
∵AC=BC,
∴AE=DE,
∵将△ADE绕点E旋转180°得△CFE,
∴△ADE≌△CFE,
∴四边形ADCF是平行四边形,
∵AE=CE,DE=EF,AE=DE,
∴AE=CE=DE=EF,
∴AC=DF,
∴四边形ADCF是矩形,
∴添加AD=DC即可使矩形ADCF是正方形,
∴当AC=BC且∠B=45°时AD=DC.
故选C.
填空题(每题3分,共24分)
11.答案:75°.
解:∵四边形ABCD是正方形,
∴AB=AD,∠DAB=90°.
∵△ABE为等边三角形,
∴AE=AB,∠EAB=60°,
∴AE=AD,∠DAE=90°-60°=30°,
∴∠AED=∠ADE=12(180°-30°)=75°.
12.答案:邻边相等的矩形是正方形.
解:∵四边形ABCD是矩形,
∴∠B=∠DAB=90°,
∵沿折痕AE翻折上去,使AB和AD边上的AF重合,
∴∠AFE=∠B=90°,AB=AF,
∵∠AFE=∠B=∠DAB=90°
∴四边形ABEF是矩形,
又∵AB=AF,
∴矩形ABEF是正方形.
13.答案:13.
解:连接AC和BD,相交于点O,如下图,
∵正方形AECF的面积为50cm2,
∴正方形AECF的边长AF=50=52(cm),
∴AC=2AF2=10(cm),
∴OA=5cm.
∵菱形的面积为ABCD的面积为120cm2,
∴12AC?BD=120,
即10BD=240,
∴BD=24(cm),
∴OB=12cm,
∴AB=OA2+OB2=52+122=13(cm),
即菱形ABCD的边长为13cm.
14.答案:4.
解:过点D作BC的垂线,交BC的延长线于点F.
∵∠ADC=∠ABC=90°,
∴∠A+∠BCD=180°.
∵∠FCD+∠BCD=180°,
∴∠A=∠FCD.
又∵∠AED=∠F=90°,AD=DC,
∴△ADE≌△CDF,
∴DE=DF.
∴四边形DEBF是正方形,S正方形DEBF=S四边形ABCD=16,
∴DE=4.
15.答案:16.
解:∵四边形ABCD是菱形,AB=4,
∴AB=BC=4.
∵∠B=60°,
∴△ABC等边三角形,
∴AC=AB=BC=4.
∵四边形ACEF是正方形,
∴AC=CE=EF=FA=4,
∴正方形ACEF的周长为4×4=16.
16.答案:n?1/4.
解:∵点A、B、C、D分别是正方形对角线的交点,
∴两个正方形之间的阴影面积为正方形总面积的1/4,
即1/4×1×1=14,
当有三个正方形时,其面积为1/4+1/4=2/4,
当有四个时,其面积为1/4+1/4+1/4=34,
所以当n个正方形时,其面积为n?1/4.
故答案为n?1/4.
17.答案:①②.
解:①②正确;
③应为“对角线垂直且相等的四边形可能是正方形,也可能是等腰梯形”,故③错误;
④应为“四条边都相等的四边形是菱形”,故④错误;
⑤中四个角都相等的四边形可能是矩形,也可能是正方形,故⑤错误.
18.答案.
解:∵ABCD是正方形,
∴OA=OD,AO⊥BD.
连接OP,易得S△AOD=S△AOP=S△ODP,即1/2OA·PE+1/2OD·PF=1/2OD·AO,
∴PE+PF=AE.
在Rt△ABD中,根据勾股定理就易得BD=
根据△ABD的面积=1/2AB·AD=1/2BD·AE,
解得AE=,则PE+PF=.
解答题(共66分)
19.证明:(1)∵四边形ABCD是平行四边形,
∴AO=CO.
∵△ACE是等边三角形,
∴EO⊥AC,即AC⊥BD,
∴四边形ABCD是菱形.
(2)∵四边形ABCD是平行四边形,
∴AO=CO.
∵△ACE是等边三角形,
∴EO平分∠AEC,
∴∠AED=1/2∠AEC=1/2×60°=30°.
∵∠AED=2∠EAD,
∴∠EAD=15°,
∴∠ADO=∠DAE+∠DEA=15°+30°=45°.
∵四边形ABCD是菱形,
∴∠ADC=2∠ADO=90°,
∴平行四边形ABCD是正方形.
20.解:(1)证明:
∵四边形ABCD是正方形
∴BC=DC,∠ABC=∠CDF=90°
∵BC=DC,∠CBE=∠CDF,BE=DF
∴△CBE≌△CDF
∴CE=CF;
(2)解:GE=BE+GD成立.理由是:
∵△CBE≌△CDF
∴∠BCE=∠DCF
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°
∵∠GCE=45°
∴∠GCF=∠GCE=45°
∵CE=CF,∠GCE=∠GCF,GC=GC
∴△ECG≌△FCG
∴GE=GF
∴GE=DF+GD=BE+GD.
21.证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠EAB=90°.
在△EAB和△FDA中,AF=DF,∠EAB=∠D,AB=AD,
∴△EAB≌△FDA,
∴BE=AF.
22.解:(1)证明:
∵四边形ABCD是正方形
∴BC=DC,∠ABC=∠CDF=90°
∵BC=DC,∠CBE=∠CDF,BE=DF
∴△CBE≌△CDF
∴CE=CF;
(2)解:GE=BE+GD成立.理由是:
∵△CBE≌△CDF
∴∠BCE=∠DCF
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°
∵∠GCE=45°
∴∠GCF=∠GCE=45°
∵CE=CF,∠GCE=∠GCF,GC=GC
∴△ECG≌△FCG
∴GE=GF
∴GE=DF+GD=BE+GD.
23.证明:(1)∵四边形ABCD是平行四边形,
∴AO=CO.
∵△ACE是等边三角形,
∴EO⊥AC,即AC⊥BD,
∴四边形ABCD是菱形.
(2)∵四边形ABCD是平行四边形,
∴AO=CO.
∵△ACE是等边三角形,
∴EO平分∠AEC,
∴∠AED=12∠AEC=12×60°=30°.
∵∠AED=2∠EAD,
∴∠EAD=15°,
∴∠ADO=∠DAE+∠DEA=15°+30°=45°.
∵四边形ABCD是菱形,
∴∠ADC=2∠ADO=90°,
∴平行四边形ABCD是正方形.
24.解:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°.
∵BH⊥AE,∠ABC=90°,
∴∠HBA+∠BAH=90°,∠ABH+∠CBF=90°,
∴∠EAB=∠FBC,
∴△ABE≌△BCF,
∴AE=BF.
(2)
∵△ABE≌△BCF,
∴BE=CF.
∵正方形的边长为5,BE=CF=2,
∴AD=CD=5,∠D=90°
∴DF=3,
∴AF=
25.
(1)证明:
∵四边形ABCD是正方形,
∴∠NAM=90°.
又∵PM⊥AD,PN⊥AB,
∴∠ANP=∠AMP=90°,
∴四边形PMAN是矩形.
∵P在AC上,
∴PM=PN,
∴四边形PMAN是正方形.
(2)
∵四边形PMAN是正方形,
∴∠MPN=∠MPE+∠EPN=90°.
∵PE⊥PB,
∴∠BPN+∠EPN=90°.
∴∠BPN=∠EPM.
在△BPN与△EPM中,
∵∠BPN=∠EPM,PN=PM,∠BNP=∠EMP=90°,
∴△BPN≌△EPM,
∴BN=EM.
