第一章 统计案例 独立性检验实习作业成果展示课件 (22张PPT)
文档属性
| 名称 | 第一章 统计案例 独立性检验实习作业成果展示课件 (22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 10:13:22 | ||
图片预览







文档简介
(共22张PPT)
人教A版选修1-2第一章实习作业
1.分类变量的定义
变量的不同“值”表示个体所属的________,像这样的变量称为分类变量.
2.2×2列联表的定义
一般地,假设有两个分类变量X和Y,它们的取值分别为________和________,其样本频数列联表
(称为2×2列联表)为:
不同类别
x1,x2
y1,y2
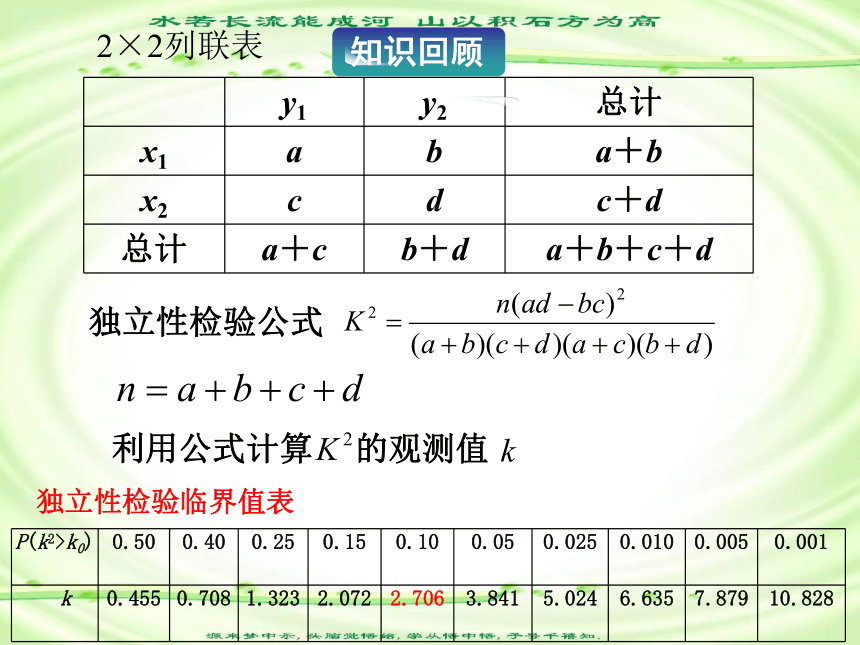
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
独立性检验临界值表
2×2列联表
独立性检验公式
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
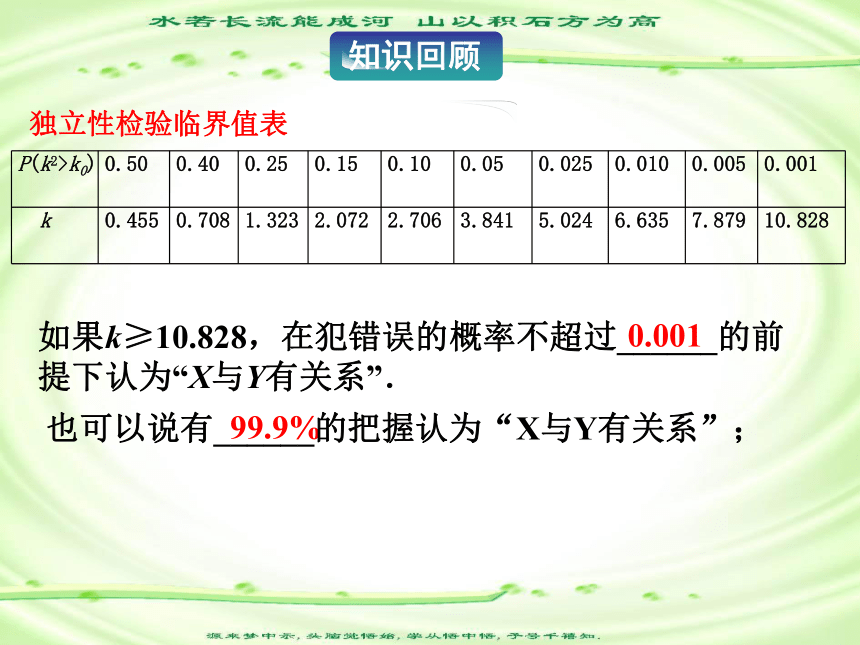
如果k≥10.828,在犯错误的概率不超过______的前提下认为“X与Y有关系”.
99.9%
独立性检验临界值表
也可以说有______的把握认为“X与Y有关系”;
0.001
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
脸上长痘与爱吃辣条的相关性调查
一 组
结论:没有充分的依据证明脸上长痘与爱吃辣条有关。
2×2列联表
脸上长痘与爱吃辣条的相关性研究
常吃 不常吃 总计
长痘 53 25 78
不长痘 33 26 59
总计 86 51 137
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
患胃病与不按时吃饭的相关性研究
二 组
所以在犯错误的概率不超过0.001的前提下认为
患胃病与不按时吃饭有关。
患胃病与不按时吃饭的相关性研究
按时吃饭 不按时吃饭 总计
患胃病 5 17 22
不患胃病 22 6 28
总计 27 23 50
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
数学成绩优秀(不低于90分)与否与课后学习时间
(不低于40分钟)的相关性调查研究
三 组
数学成绩与课后学习时间相关性研究
2X2列联表
所以在犯错误的概率不超过0.001的前提下认为
数学成绩优秀与课后学习时间长短有关系
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
不足40分钟 多于40分钟 总计
优秀 4 28 32
不优秀 46 35 81
总计 50 63 113
喜欢玩电子游戏与性别的相关性调查研究
四 组
喜欢玩电子游戏与性别的相关性研究
2X2列联表
所以在犯错误的概率不超过0.001的前提下认为
喜欢玩电子游戏与性别有关。
男生 女生 总计
喜欢 161 38 199
不喜欢 13 107 120
总计 174 145 319
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
高中生近视眼与父母近视的相关性调查研究
五 组
高中生近视与父母近视的相关性研究
2X2列联表
所以在犯错误的概率不超过0.01的前提下认为
高中生近视与父母近视有关系。
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
父母不近视 父或母近视 总计
孩子近视 211 75 286
孩子不近视 76 11 87
总计 287 86 373
课堂实践 现场对我们班同学“喜欢体育运动与性别是否有关系?”进行调查并统计下表:
试用你所学过的知识进行分析,能否在犯错误的概率不超过0.005的前提下,认为“喜欢体育与否与性别有关系”?
喜欢 不喜欢 合计
男生
女生
合计
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
1.网购与性别是否有关
2.买保险与性别是否有关
3.拍抖音视频与年龄(30岁为界)是否有关
人教A版选修1-2第一章实习作业
1.分类变量的定义
变量的不同“值”表示个体所属的________,像这样的变量称为分类变量.
2.2×2列联表的定义
一般地,假设有两个分类变量X和Y,它们的取值分别为________和________,其样本频数列联表
(称为2×2列联表)为:
不同类别
x1,x2
y1,y2
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
独立性检验临界值表
2×2列联表
独立性检验公式
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
如果k≥10.828,在犯错误的概率不超过______的前提下认为“X与Y有关系”.
99.9%
独立性检验临界值表
也可以说有______的把握认为“X与Y有关系”;
0.001
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
脸上长痘与爱吃辣条的相关性调查
一 组
结论:没有充分的依据证明脸上长痘与爱吃辣条有关。
2×2列联表
脸上长痘与爱吃辣条的相关性研究
常吃 不常吃 总计
长痘 53 25 78
不长痘 33 26 59
总计 86 51 137
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
患胃病与不按时吃饭的相关性研究
二 组
所以在犯错误的概率不超过0.001的前提下认为
患胃病与不按时吃饭有关。
患胃病与不按时吃饭的相关性研究
按时吃饭 不按时吃饭 总计
患胃病 5 17 22
不患胃病 22 6 28
总计 27 23 50
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
数学成绩优秀(不低于90分)与否与课后学习时间
(不低于40分钟)的相关性调查研究
三 组
数学成绩与课后学习时间相关性研究
2X2列联表
所以在犯错误的概率不超过0.001的前提下认为
数学成绩优秀与课后学习时间长短有关系
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
不足40分钟 多于40分钟 总计
优秀 4 28 32
不优秀 46 35 81
总计 50 63 113
喜欢玩电子游戏与性别的相关性调查研究
四 组
喜欢玩电子游戏与性别的相关性研究
2X2列联表
所以在犯错误的概率不超过0.001的前提下认为
喜欢玩电子游戏与性别有关。
男生 女生 总计
喜欢 161 38 199
不喜欢 13 107 120
总计 174 145 319
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
高中生近视眼与父母近视的相关性调查研究
五 组
高中生近视与父母近视的相关性研究
2X2列联表
所以在犯错误的概率不超过0.01的前提下认为
高中生近视与父母近视有关系。
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
父母不近视 父或母近视 总计
孩子近视 211 75 286
孩子不近视 76 11 87
总计 287 86 373
课堂实践 现场对我们班同学“喜欢体育运动与性别是否有关系?”进行调查并统计下表:
试用你所学过的知识进行分析,能否在犯错误的概率不超过0.005的前提下,认为“喜欢体育与否与性别有关系”?
喜欢 不喜欢 合计
男生
女生
合计
P(k2>k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
1.网购与性别是否有关
2.买保险与性别是否有关
3.拍抖音视频与年龄(30岁为界)是否有关
