1.1.3 四种命题间的相互关系 课件 20张PPT
文档属性
| 名称 | 1.1.3 四种命题间的相互关系 课件 20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 723.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-02 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
1.1.3 四种命题间的相互关系
在数学中我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题。其中判断为真的语句叫做真命题,判断为假的语句叫做假命题
复习命题的定义
下列四个命题中,命题(1)与命题(2)(3)(4)的条件和结论之间分别有什么关系?
若f(x)是正弦函数,则f(x)是周期函数;
若f(x)是周期函数,则f(x)是正弦函数;
若f(x)不是正弦函数,则f(x)不是周期函数;
若f(x)不是周期函数,则f(x)不是正弦函数。
命题(1)与命题(2)的条件和结论之间分别有什么关系?
互逆命题:一个命题的条件和结论分别是另一个命题的结论和条件,这两个命题叫做互逆命题。其中一个命题叫做原命题。另一个命题叫做原命题的逆命题。
即 原命题:若p,则q
逆命题:若q,则p
若p,则q
若q,则p
若┐p,则┐q
若┐q, 则┐p
四种命题
原命题:
逆命题:
否命题:
逆否命题:
观察与思考
?
你能说出其中任意两个命题之间的关系吗?
若f(x)是正弦函数,则f(x)是周期函数;
若f(x)是周期函数,则f(x)是正弦函数;
若f(x)不是正弦函数,则f(x)不是周期函数;
若f(x)不是周期函数,则f(x)不是正弦函数.
若p,则q
若q,则p
若┐p,则┐q
若┐q, 则┐p
四种命题
原命题:
逆命题:
否命题:
逆否命题:
你能说出其中任意两个命题之间的关系吗?
任意两个命题之间的关系
原命题:若p则q
逆命题:若q则p
否命题:若非p则非q
逆否命题:若非q则非p
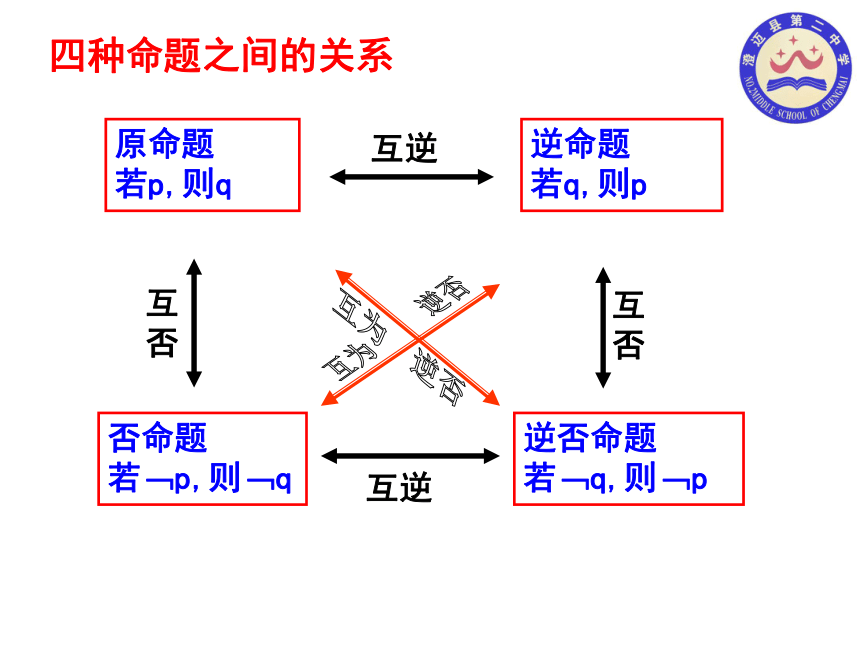
四种命题之间的关系
原命题
若p,则q
逆命题
若q,则p
否命题
若﹁p,则﹁q
逆否命题
若﹁q,则﹁p
互逆
互否
互否
互逆
是真命题
是真命题
是真命题
是真命题
是真命题
是真命题
是假命题
是假命题
四种命题的真假性之间有什么规律吗?
是真命题
是假命题
是假命题
是真命题
是假命题
是假命题
是假命题
是假命题
一般地,四种命题的真假性,有而且仅有下面四种情况:
互为逆命题的两个命题真假性没有关系。
互为否命题的两个命题真假性没有关系。
原命题与其逆否命题同真假.
一个命题的逆命题与否命题同真假.
原命题 逆命题 否命题 逆否命题
真 真 真 真
真 假 假 真
假 真 真 假
假 假 假 假
1.判断下列说法是否正确.
(1)一个命题的逆命题为真,它的逆否命题不一定
为真;
(对)
(2)一个命题的否命题为真,它的逆命题一定为真.
(对)
(3)一个命题的原命题为假,它的逆命题一定为假.
(错)
(4)一个命题的逆否命题为假,它的否命题为假.
(错)
2.命题“若△ABC的两个内角相等,则它是等腰三角形”
的逆否命题是 命题(填“真”或“假”).
真
逆否命题是“若△ABC不是等腰三角形,则它的任何两个
内角都不相等”
【提升总结】因为原命题和它的逆否命题有相同的 真假性,所以当直接证明某一命题为真命题有困难 时,可以通过证明它的逆否命题为真命题,来间接
证明原命题为真命题.
例3 证明:若x2+y2=0,则x=y=0.
证明:若x,y中至少有一个不为0,不妨设x≠0,则x2>0,所以x2+y2 >0, 也就是说x2+y2 ≠0. 因此,原命题的逆否命题为真命题,从而原命题为真命题.
课堂练习
课本 8页 练习
证明:若a2-b2+2a-4b-3≠0,则a-b≠1
证明:若a-b=1,则a2-b2+2a-4b-3
=(a+b)(a-b)+2(a-b)-2b-3
=(a-b)-1=0成立, ∴根据逆否命题的等价性可知: 若a2-b2+2a-4b-3 ≠0,则a-b≠1成立.
1.四种命题之间的关系
原命题
若p,则q
逆命题
若q,则p
否命题
若﹁p,则﹁q
逆否命题
若﹁q,则﹁p
互逆
互否
互否
互逆
2.四种命题真假之间的关系
互为逆命题的两个命题真假性没有关系。
互为否命题的两个命题真假性没有关系。
原命题与其逆否命题同真假.
一个命题的逆命题与否命题同真假.
3.一种间接证明法
要证明一个命题,可以证它的逆否命题
课堂作业
1.课本 30页 复习参考题 A组 1
2.课本 8页 习题1.1 A组 4
下列说法中错误的一项是( )
A. 一个命题的原命题为真,它的逆命题不一定为真;
B. 一个命题的原命题为假,它的否命题不一定为真;
C. 一个命题的否命题为真,它的逆命题一定为假;
D. 一个命题的原命题为真,它的逆否命题一定为真.
下列说法
(1)四种命题中真命题的个数一定是偶数;
(2) 若一个命题的逆命题是真命题,则它的否命题不一定是真命题
(3) 逆命题与否命题之间是互为逆否关系;
(4) 若一个命题的逆否命题是假命题,则它的逆命题与否命题都是假命题.
其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
1.1.3 四种命题间的相互关系
在数学中我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题。其中判断为真的语句叫做真命题,判断为假的语句叫做假命题
复习命题的定义
下列四个命题中,命题(1)与命题(2)(3)(4)的条件和结论之间分别有什么关系?
若f(x)是正弦函数,则f(x)是周期函数;
若f(x)是周期函数,则f(x)是正弦函数;
若f(x)不是正弦函数,则f(x)不是周期函数;
若f(x)不是周期函数,则f(x)不是正弦函数。
命题(1)与命题(2)的条件和结论之间分别有什么关系?
互逆命题:一个命题的条件和结论分别是另一个命题的结论和条件,这两个命题叫做互逆命题。其中一个命题叫做原命题。另一个命题叫做原命题的逆命题。
即 原命题:若p,则q
逆命题:若q,则p
若p,则q
若q,则p
若┐p,则┐q
若┐q, 则┐p
四种命题
原命题:
逆命题:
否命题:
逆否命题:
观察与思考
?
你能说出其中任意两个命题之间的关系吗?
若f(x)是正弦函数,则f(x)是周期函数;
若f(x)是周期函数,则f(x)是正弦函数;
若f(x)不是正弦函数,则f(x)不是周期函数;
若f(x)不是周期函数,则f(x)不是正弦函数.
若p,则q
若q,则p
若┐p,则┐q
若┐q, 则┐p
四种命题
原命题:
逆命题:
否命题:
逆否命题:
你能说出其中任意两个命题之间的关系吗?
任意两个命题之间的关系
原命题:若p则q
逆命题:若q则p
否命题:若非p则非q
逆否命题:若非q则非p
四种命题之间的关系
原命题
若p,则q
逆命题
若q,则p
否命题
若﹁p,则﹁q
逆否命题
若﹁q,则﹁p
互逆
互否
互否
互逆
是真命题
是真命题
是真命题
是真命题
是真命题
是真命题
是假命题
是假命题
四种命题的真假性之间有什么规律吗?
是真命题
是假命题
是假命题
是真命题
是假命题
是假命题
是假命题
是假命题
一般地,四种命题的真假性,有而且仅有下面四种情况:
互为逆命题的两个命题真假性没有关系。
互为否命题的两个命题真假性没有关系。
原命题与其逆否命题同真假.
一个命题的逆命题与否命题同真假.
原命题 逆命题 否命题 逆否命题
真 真 真 真
真 假 假 真
假 真 真 假
假 假 假 假
1.判断下列说法是否正确.
(1)一个命题的逆命题为真,它的逆否命题不一定
为真;
(对)
(2)一个命题的否命题为真,它的逆命题一定为真.
(对)
(3)一个命题的原命题为假,它的逆命题一定为假.
(错)
(4)一个命题的逆否命题为假,它的否命题为假.
(错)
2.命题“若△ABC的两个内角相等,则它是等腰三角形”
的逆否命题是 命题(填“真”或“假”).
真
逆否命题是“若△ABC不是等腰三角形,则它的任何两个
内角都不相等”
【提升总结】因为原命题和它的逆否命题有相同的 真假性,所以当直接证明某一命题为真命题有困难 时,可以通过证明它的逆否命题为真命题,来间接
证明原命题为真命题.
例3 证明:若x2+y2=0,则x=y=0.
证明:若x,y中至少有一个不为0,不妨设x≠0,则x2>0,所以x2+y2 >0, 也就是说x2+y2 ≠0. 因此,原命题的逆否命题为真命题,从而原命题为真命题.
课堂练习
课本 8页 练习
证明:若a2-b2+2a-4b-3≠0,则a-b≠1
证明:若a-b=1,则a2-b2+2a-4b-3
=(a+b)(a-b)+2(a-b)-2b-3
=(a-b)-1=0成立, ∴根据逆否命题的等价性可知: 若a2-b2+2a-4b-3 ≠0,则a-b≠1成立.
1.四种命题之间的关系
原命题
若p,则q
逆命题
若q,则p
否命题
若﹁p,则﹁q
逆否命题
若﹁q,则﹁p
互逆
互否
互否
互逆
2.四种命题真假之间的关系
互为逆命题的两个命题真假性没有关系。
互为否命题的两个命题真假性没有关系。
原命题与其逆否命题同真假.
一个命题的逆命题与否命题同真假.
3.一种间接证明法
要证明一个命题,可以证它的逆否命题
课堂作业
1.课本 30页 复习参考题 A组 1
2.课本 8页 习题1.1 A组 4
下列说法中错误的一项是( )
A. 一个命题的原命题为真,它的逆命题不一定为真;
B. 一个命题的原命题为假,它的否命题不一定为真;
C. 一个命题的否命题为真,它的逆命题一定为假;
D. 一个命题的原命题为真,它的逆否命题一定为真.
下列说法
(1)四种命题中真命题的个数一定是偶数;
(2) 若一个命题的逆命题是真命题,则它的否命题不一定是真命题
(3) 逆命题与否命题之间是互为逆否关系;
(4) 若一个命题的逆否命题是假命题,则它的逆命题与否命题都是假命题.
其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
