高中数学选修2-1第二章 圆锥曲线与方程 用《几何画板》探究点的轨迹:椭圆 课件 21张PPT
文档属性
| 名称 | 高中数学选修2-1第二章 圆锥曲线与方程 用《几何画板》探究点的轨迹:椭圆 课件 21张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-02 11:35:18 | ||
图片预览





文档简介
(共21张PPT)
椭圆及其标准方程
高二数学人教版选修2-1
观察
演示
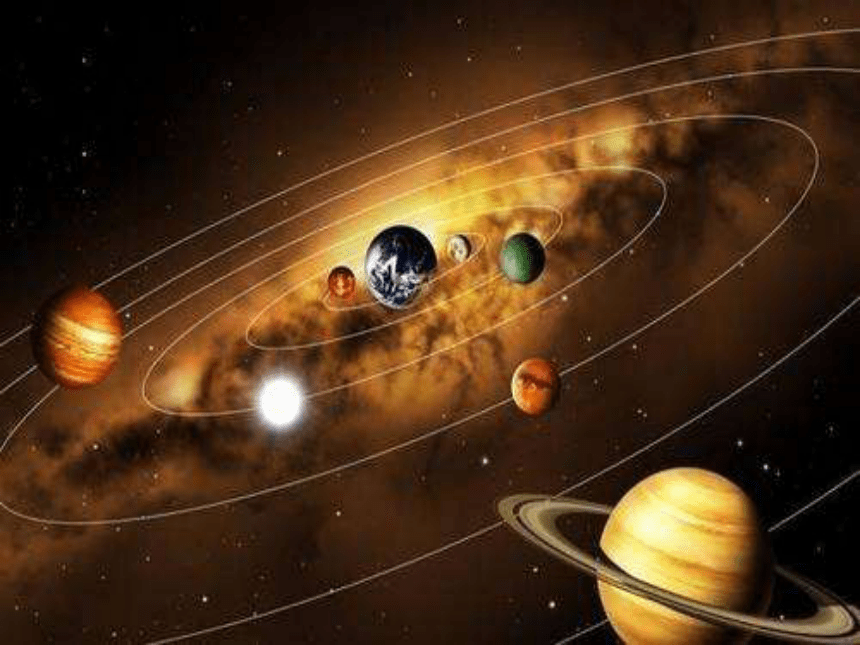
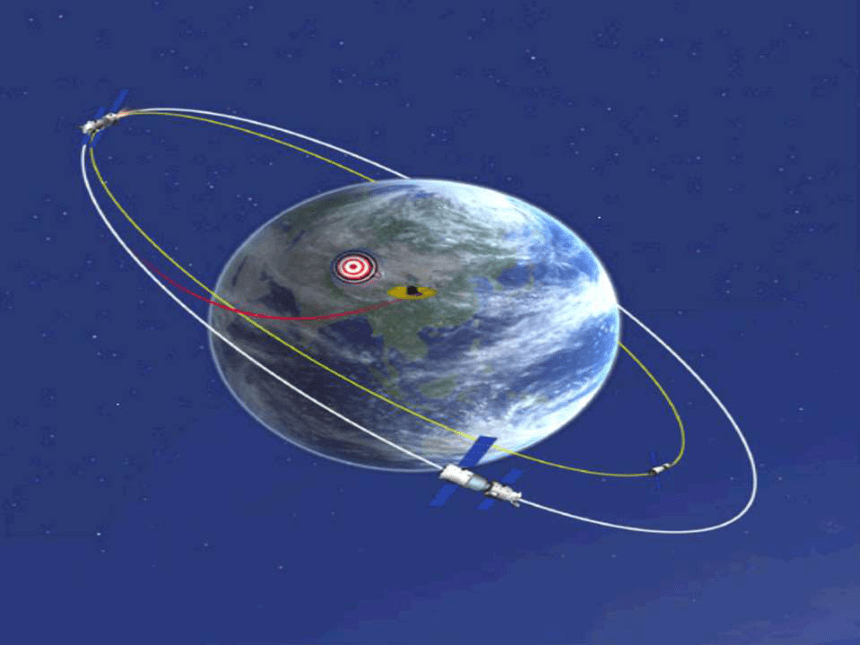
有哪些生活经验能得到椭圆
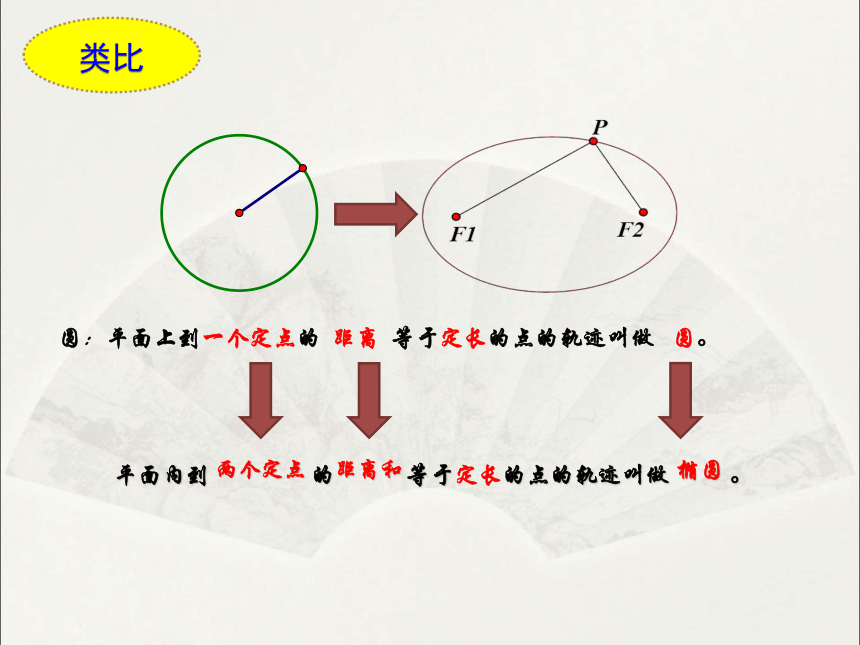
类比
圆:平面上到一个定点的 距离 等于定长的点的轨迹叫做 圆。
平面内到 的 等于定长的点的轨迹叫做 。
两个定点
距离和
椭圆
平面内到两个定点的距离和等于定长的点的轨迹叫做椭圆。
大于两定点距离
这两个定点F1、F2叫做焦点,两焦点的距离叫做焦距。
当 时,轨迹是线段。
椭圆:平面内到两个定点的距离和等于常数(大于两定点距离)的点的轨迹。
当 时,轨迹不存在。
探究一:椭圆的定义
例1
(1)平面内到A(-3,0),B(3,0)距离和等于8的点的轨迹
(2)平面内到A(-3,0),B(3,0)距离和等于6的点的轨迹
线段AB
椭圆
(3)平面内到A(-3,0),B(3,0)距离和等于5的点的轨迹
不存在
建系:
设点:
列式:
化简:
证明:
建立适当的直角坐标系;
设M(x,y)是曲线上任意一点;
建立关于x,y的方程 f(x,y)=0;
化简方程f(x,y)=0.
说明曲线上的点都符合条件,(纯粹性);符合条件的点都在曲线上(完备性)。
探究二:求椭圆的标准方程
复习:求曲线方程的方法步骤是什么?
? 探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则:“对称”、“简洁”
M
F1
F2
方案一
O
x
y
方案二
F1
F2
M
如何求椭圆的方程?
思考:
y
x
O
y
x
O
y
x
O
x
F1
F2
M
0
y
解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),M与F1和F2的距离的和等于正常数2a (2a>2c) ,则F1、F2的坐标分别 是(?c,0)、(c,0) .
由椭圆的定义得:
代入坐标
(问题:下面怎样化简?)
由椭圆定义可知
两边再平方,得
移项,再平方
).
0
(
1
2
2
2
2
>
>
=
+
b
a
b
y
a
x
椭圆的标准方程
它表示:
① 椭圆的焦点在x轴
② 焦点坐标为F1(-C,0)、F2(C,0)
③ c2= a2 - b2
焦点在x轴上的椭圆的标准方程:
F1
F2
M
0
x
y
焦点在y轴上的椭圆的标准方程
它表示:
① 椭圆的焦点在y轴
② 焦点是F1(0,-c)、 F2(0,c)
③ c2= a2 - b2
x
M
F1
F2
y
O
思考:当椭圆的焦点在y轴上时,它的标准方程是怎样的呢
分母哪个大,焦点就在哪个轴上
平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹
标准方程
相 同 点
焦点位置的判断
不 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
根据所学知识完成下表:
x
y
F1
F2
P
O
x
y
F1
F2
P
O
a2-c2=b2
椭圆的两个焦点的坐标分别是F1(-2,0),F2(2,0)椭圆过点M ( , ) ,求椭圆的标准方程及三角形MF1F2的周长。
1
2
y
o
F
F
M
x
求椭圆标准方程的解题步骤:
(1)一定焦点位置
(2)二设椭圆方程;
(3)三求a、b的值.(待定系数法)
(4)写出椭圆的标准方程.
例2
B
C
D
A
7
5
A
3
2
练习1.已知椭圆 上一点P到椭圆的一个焦点的距离为3,则P到另一个焦点的距离为 ( )
2.求适合下列条件的椭圆的标准方程
(1)a= ,b=1,焦点在x轴上,
(2)焦点为F1(0,-3),F2(0,3),且a=5.
如图,点C(2,0)为圆A 半径AB上一点,点M在圆上,作MC的中垂线交AM于点P,当M在圆上运动时,点P的轨迹方程是什么?
思考
提示∵PC+PA=PM+PA= R >AC,
∴P点轨迹为椭圆。
定义
椭圆定义:平面内与两个定点F1、F2的距离的和等于
常数2a (大于│ F1F2│,)的点的轨迹,叫做椭圆.
两个方程
椭圆标准方程:
(1). 椭圆焦点在x轴上
(2). 椭圆焦点在y轴上
求曲线方程的步骤:建系、设点、列式、化简、证明。
作业
1、预习例2
2、书面作业:
(1)课本42面第2题
(2) B组第一题
3、查找生活的椭圆并利用信息技术知识探究与椭圆有关的知识
谢谢大家
椭圆及其标准方程
高二数学人教版选修2-1
观察
演示
有哪些生活经验能得到椭圆
类比
圆:平面上到一个定点的 距离 等于定长的点的轨迹叫做 圆。
平面内到 的 等于定长的点的轨迹叫做 。
两个定点
距离和
椭圆
平面内到两个定点的距离和等于定长的点的轨迹叫做椭圆。
大于两定点距离
这两个定点F1、F2叫做焦点,两焦点的距离叫做焦距。
当 时,轨迹是线段。
椭圆:平面内到两个定点的距离和等于常数(大于两定点距离)的点的轨迹。
当 时,轨迹不存在。
探究一:椭圆的定义
例1
(1)平面内到A(-3,0),B(3,0)距离和等于8的点的轨迹
(2)平面内到A(-3,0),B(3,0)距离和等于6的点的轨迹
线段AB
椭圆
(3)平面内到A(-3,0),B(3,0)距离和等于5的点的轨迹
不存在
建系:
设点:
列式:
化简:
证明:
建立适当的直角坐标系;
设M(x,y)是曲线上任意一点;
建立关于x,y的方程 f(x,y)=0;
化简方程f(x,y)=0.
说明曲线上的点都符合条件,(纯粹性);符合条件的点都在曲线上(完备性)。
探究二:求椭圆的标准方程
复习:求曲线方程的方法步骤是什么?
? 探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则:“对称”、“简洁”
M
F1
F2
方案一
O
x
y
方案二
F1
F2
M
如何求椭圆的方程?
思考:
y
x
O
y
x
O
y
x
O
x
F1
F2
M
0
y
解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),M与F1和F2的距离的和等于正常数2a (2a>2c) ,则F1、F2的坐标分别 是(?c,0)、(c,0) .
由椭圆的定义得:
代入坐标
(问题:下面怎样化简?)
由椭圆定义可知
两边再平方,得
移项,再平方
).
0
(
1
2
2
2
2
>
>
=
+
b
a
b
y
a
x
椭圆的标准方程
它表示:
① 椭圆的焦点在x轴
② 焦点坐标为F1(-C,0)、F2(C,0)
③ c2= a2 - b2
焦点在x轴上的椭圆的标准方程:
F1
F2
M
0
x
y
焦点在y轴上的椭圆的标准方程
它表示:
① 椭圆的焦点在y轴
② 焦点是F1(0,-c)、 F2(0,c)
③ c2= a2 - b2
x
M
F1
F2
y
O
思考:当椭圆的焦点在y轴上时,它的标准方程是怎样的呢
分母哪个大,焦点就在哪个轴上
平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹
标准方程
相 同 点
焦点位置的判断
不 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
根据所学知识完成下表:
x
y
F1
F2
P
O
x
y
F1
F2
P
O
a2-c2=b2
椭圆的两个焦点的坐标分别是F1(-2,0),F2(2,0)椭圆过点M ( , ) ,求椭圆的标准方程及三角形MF1F2的周长。
1
2
y
o
F
F
M
x
求椭圆标准方程的解题步骤:
(1)一定焦点位置
(2)二设椭圆方程;
(3)三求a、b的值.(待定系数法)
(4)写出椭圆的标准方程.
例2
B
C
D
A
7
5
A
3
2
练习1.已知椭圆 上一点P到椭圆的一个焦点的距离为3,则P到另一个焦点的距离为 ( )
2.求适合下列条件的椭圆的标准方程
(1)a= ,b=1,焦点在x轴上,
(2)焦点为F1(0,-3),F2(0,3),且a=5.
如图,点C(2,0)为圆A 半径AB上一点,点M在圆上,作MC的中垂线交AM于点P,当M在圆上运动时,点P的轨迹方程是什么?
思考
提示∵PC+PA=PM+PA= R >AC,
∴P点轨迹为椭圆。
定义
椭圆定义:平面内与两个定点F1、F2的距离的和等于
常数2a (大于│ F1F2│,)的点的轨迹,叫做椭圆.
两个方程
椭圆标准方程:
(1). 椭圆焦点在x轴上
(2). 椭圆焦点在y轴上
求曲线方程的步骤:建系、设点、列式、化简、证明。
作业
1、预习例2
2、书面作业:
(1)课本42面第2题
(2) B组第一题
3、查找生活的椭圆并利用信息技术知识探究与椭圆有关的知识
谢谢大家
