高中数学 人教新课标A版 选修2-2 第一章 导数及其应用 曲边梯形的面积 课件 28张PPT
文档属性
| 名称 | 高中数学 人教新课标A版 选修2-2 第一章 导数及其应用 曲边梯形的面积 课件 28张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 17:31:53 | ||
图片预览




文档简介
(共28张PPT)
信息技术应用
曲边梯形的面积
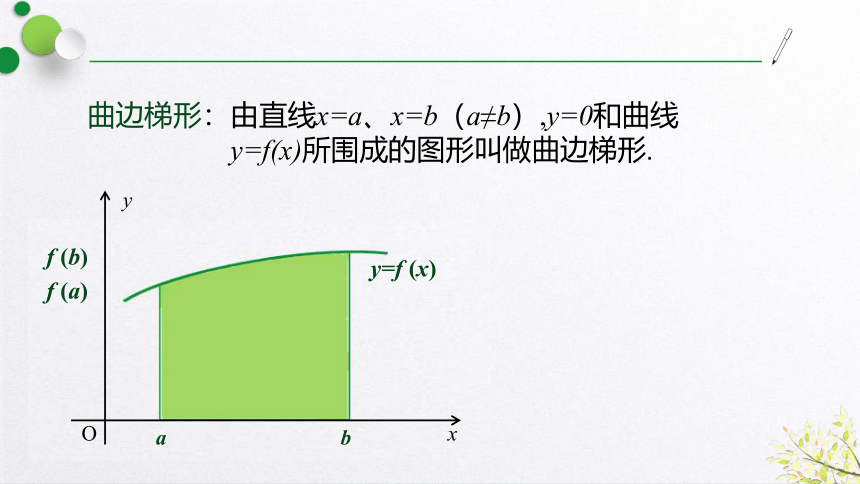
曲边梯形:由直线x=a、x=b(a≠b),y=0和曲线
y=f(x)所围成的图形叫做曲边梯形.
O
x
y
a
b
y=f (x)
f (a)
f (b)
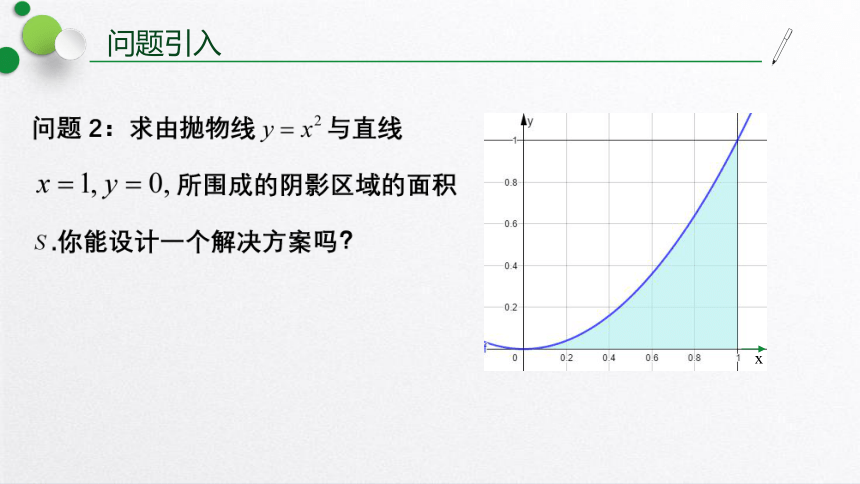
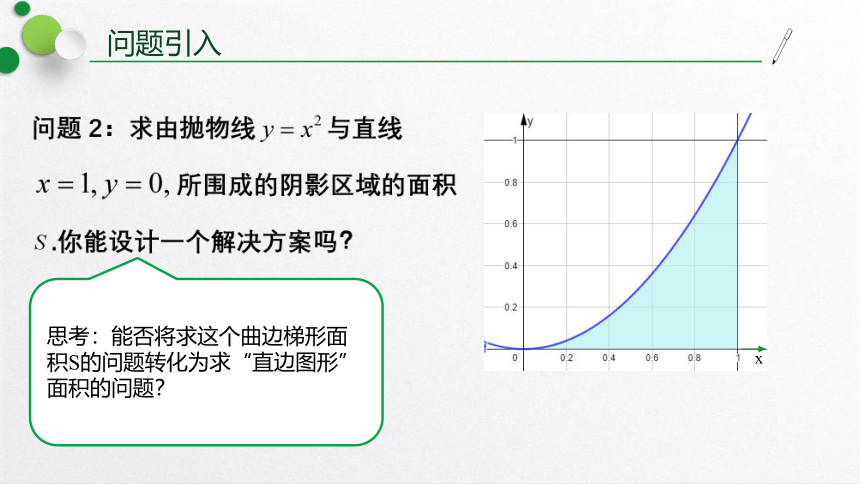
问题引入
x
问题引入
x
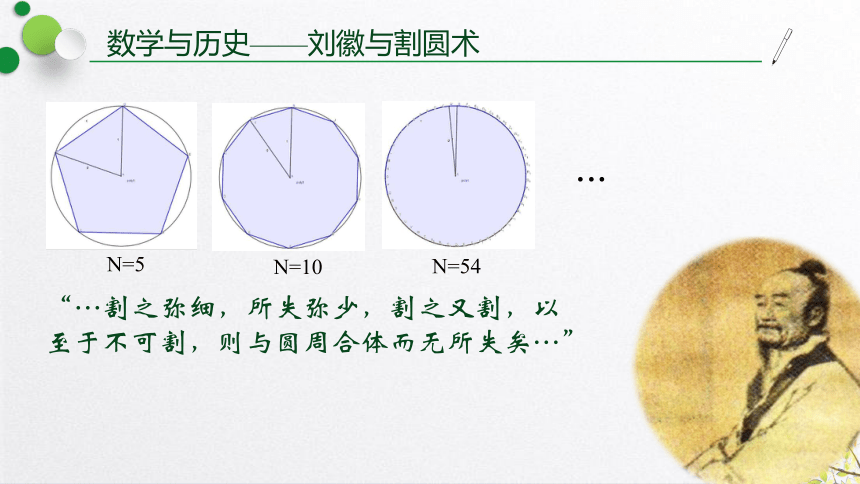
数学与历史——刘徽与割圆术
数学与历史——刘徽与割圆术
N=5
N=10
N=54
???
“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”
问题引入
x
思考:能否将求这个曲边梯形面积S的问题转化为求“直边图形”面积的问题?
思考1:能否将求这个曲边梯形面积S的问题转化为求“直边图形”面积的问题?
操作实践
在区间[0,1]分成n个小区间:
(1)在区间[0,1]上插入 个点,将它分成n个小区间:
,记第i个区间为 ,其长度为
(2)分别过上述n-1个分点作x轴的垂线,把曲边梯形分成
n个小梯形,它们的面积记作:
显然,
化整为零
一、分割
第i个 小曲边梯形
在局部小范围内“以直代曲”
二、近似代替
操作实践
二、近似代替
操作实践
以直代曲
三、求和
操作实践
积零为整
四、取极限
操作实践
方法启迪
1
分割
2
近似代替
3
求和
4
取极限
分割————化整为零
近似代替——以直代曲
求和————积零为整
取极限———无限逼近
特例探究
四、取极限
思考:两种情况计算出的结果一模一样,这说明了什么?
课后作业:
1. 求由直线x=0,x=2,y=0和曲线y=x?所围成的曲边梯形的面积S?
课堂小结——知识与方法小结
1
分割
2
近似代替
3
求和
4
取极限
分割————化整为零
近似代替——以直代曲
求和————积零为整
取极限———无限逼近
对立与统一
极限思想方法
课堂小结——思想小结
1
2
近似代替
3
聆
听
谢
谢
方法启迪
1
分割
2
近似代替
3
求和
4
取极限
信息技术应用
曲边梯形的面积
曲边梯形:由直线x=a、x=b(a≠b),y=0和曲线
y=f(x)所围成的图形叫做曲边梯形.
O
x
y
a
b
y=f (x)
f (a)
f (b)
问题引入
x
问题引入
x
数学与历史——刘徽与割圆术
数学与历史——刘徽与割圆术
N=5
N=10
N=54
???
“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”
问题引入
x
思考:能否将求这个曲边梯形面积S的问题转化为求“直边图形”面积的问题?
思考1:能否将求这个曲边梯形面积S的问题转化为求“直边图形”面积的问题?
操作实践
在区间[0,1]分成n个小区间:
(1)在区间[0,1]上插入 个点,将它分成n个小区间:
,记第i个区间为 ,其长度为
(2)分别过上述n-1个分点作x轴的垂线,把曲边梯形分成
n个小梯形,它们的面积记作:
显然,
化整为零
一、分割
第i个 小曲边梯形
在局部小范围内“以直代曲”
二、近似代替
操作实践
二、近似代替
操作实践
以直代曲
三、求和
操作实践
积零为整
四、取极限
操作实践
方法启迪
1
分割
2
近似代替
3
求和
4
取极限
分割————化整为零
近似代替——以直代曲
求和————积零为整
取极限———无限逼近
特例探究
四、取极限
思考:两种情况计算出的结果一模一样,这说明了什么?
课后作业:
1. 求由直线x=0,x=2,y=0和曲线y=x?所围成的曲边梯形的面积S?
课堂小结——知识与方法小结
1
分割
2
近似代替
3
求和
4
取极限
分割————化整为零
近似代替——以直代曲
求和————积零为整
取极限———无限逼近
对立与统一
极限思想方法
课堂小结——思想小结
1
2
近似代替
3
聆
听
谢
谢
方法启迪
1
分割
2
近似代替
3
求和
4
取极限
