高中数学人教新课标A版选修2-3随机变量及其分布列复习课件 19张PPT
文档属性
| 名称 | 高中数学人教新课标A版选修2-3随机变量及其分布列复习课件 19张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 17:21:16 | ||
图片预览



文档简介
(共19张PPT)
随机变量及其分布列
章末复习
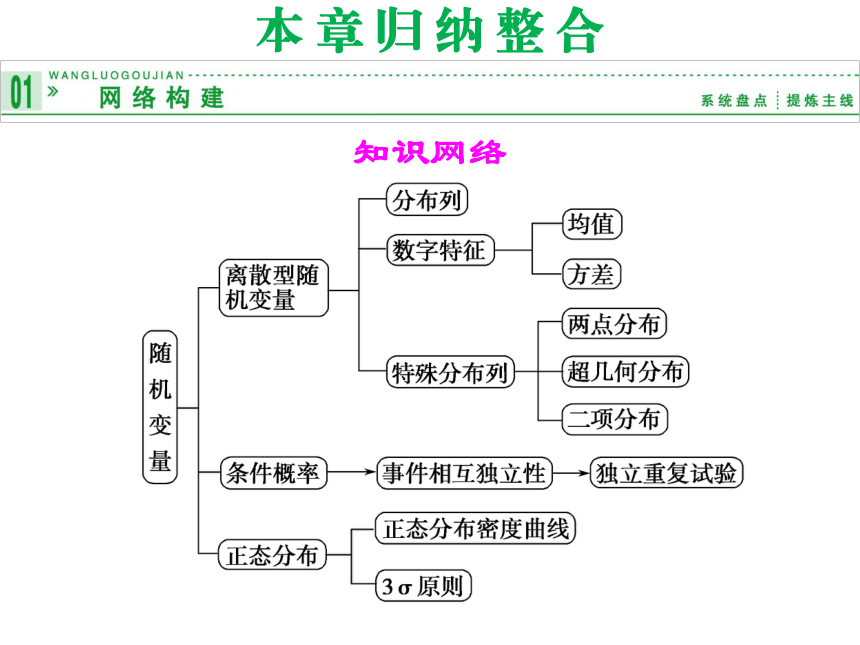
知识网络
本 章 归 纳 整 合
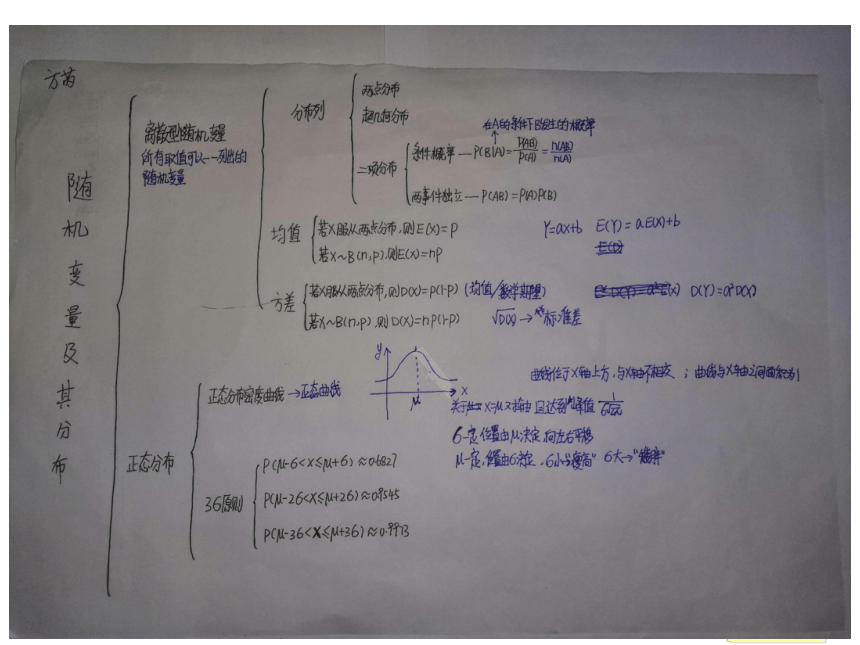
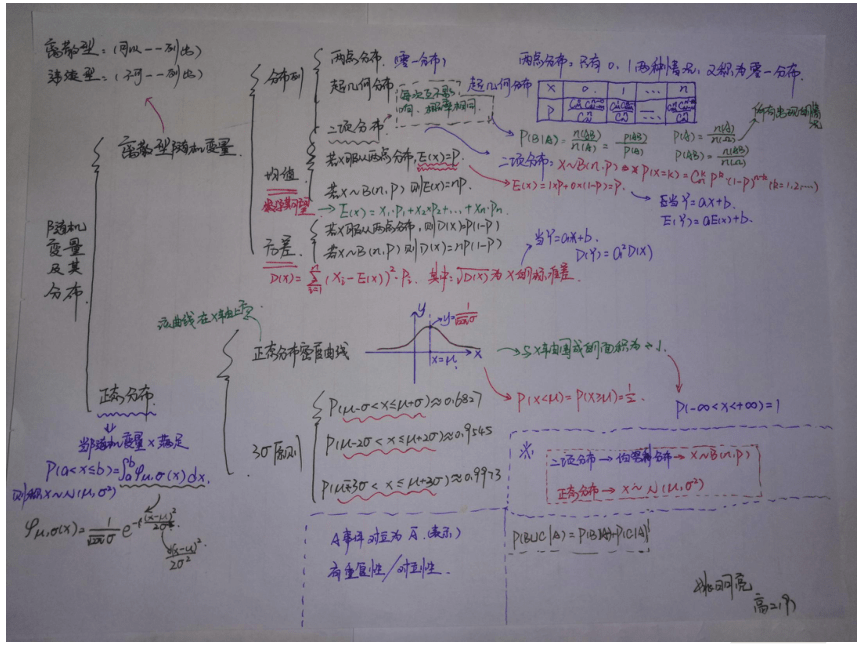
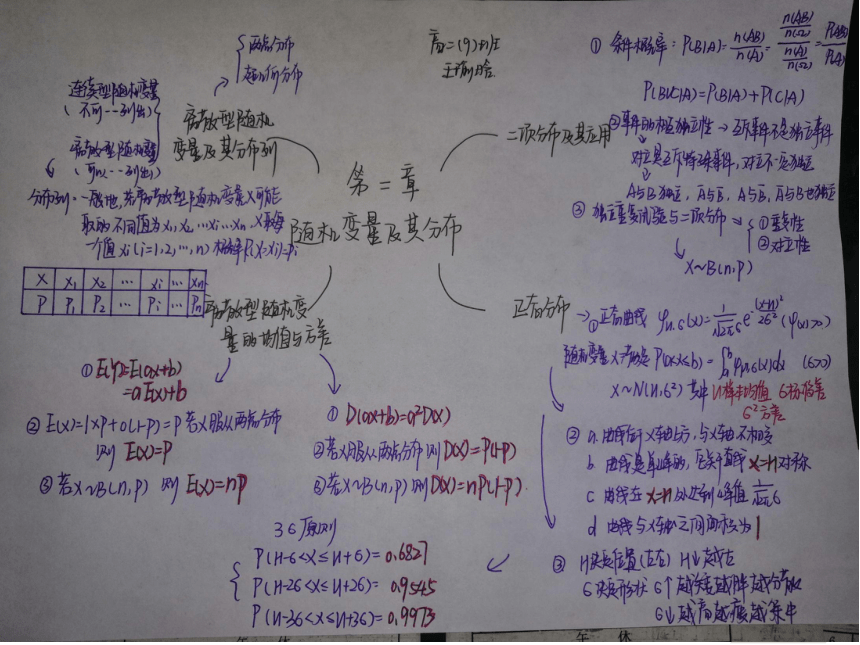
知识网络
1、离散型随机变量的分布列在高中阶段主要学习的有:超几何分布,二项分布,两点分布。
2、对于分布列的求法,其难点在于每个随机变量取值时相关概率的求法,计算可能会用到等可能事件、互斥事件、相互独立事件的概率公式等.
3、均值与方差都是随机变量重要的数字特征,方差是建立在均值这一概念之上的,它表明了随机变量所取的值相对于它的均值的集中与离散程度,二者联系密切,在现实生产生活中特别是风险决策中有着重要意义.
专题一 离散型随机变量的分布列、均值与方差
类型一 离散型随机变量的分布列、均值和方差
袋中有4个红球,2个黑球,从中任取3个小球,并记录其颜色.
(1)求取到黑球个数X1的均值与方差;
(2)若每次取出1个球后放回,连续取3次,求取到黑球个数X2的均值与方差;
(3)在(2)的基础上,取出1个黑球计2分,取出白球不得分,求所得分数Y的均值与方差.
【例1】
专题二 条件概率
在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
解 设“第1次抽到理科题”为事件A,“第2次抽到理科题”为事件B,则“第1次和第2次都抽到理科题”为事件AB.
【例2】
类型二 条件概率的求法
求相互独立事件一般与互斥事件、对立事件结合在一起进行考查,解答此类问题时应分清事件间的内部联系,在些基础上用基本事件之间的交、并、补运算表示出有关事件,并运用相应公式求解.
特别注意以下两公式的使用前提
(1)若A,B互斥,则P(A∪B)=P(A)+P(B),反之不成立.
(2)若A,B相互独立,则P(AB)=P(A)P(B),反之成立.
专题三 相互独立事件的概率
1.
2.
类型三 求相互独立事件的概率
在某次1500米体能测试中,甲、乙、丙三人各自通过测试的概率分别为 ,求:
(1)3人都通过体能测试的概率;
(2)恰有2人通过体能测试的概率.
【例3】
解 设A表示事件“甲通过体能测试”,
B表示事件“乙通过体能测试”,
C表示事件“丙通过体能测试”.
(1)设M1表示事件“甲、乙、丙3人都通过体能测试”,
即M1=ABC.
由事件A,B,C相互独立,可得:
(2)设M2表示事件“甲、乙、丙3人中只有2人通过体能测试”,
正态密度曲线恰好关于参数μ对称,因此充分利用该图形的对称性及3个特殊区间内的概率值来求解其他区间的概率值,是一种非常简捷的方式.
专题四 正态分布
某市去年高考考生成绩X服从正态分布N(500,502),现有25 000名考生,试确定考生成绩在550~600分的人数.
【例4】
类型四 正态分布
03 真题放送
(2016.四川高考)同时抛掷两枚质地均匀的硬币,当至少有一枚硬币正面向上时,就说这次实验成功,则在2次试验中成功次数X的均值是______.
随机变量及其分布列
章末复习
知识网络
本 章 归 纳 整 合
知识网络
1、离散型随机变量的分布列在高中阶段主要学习的有:超几何分布,二项分布,两点分布。
2、对于分布列的求法,其难点在于每个随机变量取值时相关概率的求法,计算可能会用到等可能事件、互斥事件、相互独立事件的概率公式等.
3、均值与方差都是随机变量重要的数字特征,方差是建立在均值这一概念之上的,它表明了随机变量所取的值相对于它的均值的集中与离散程度,二者联系密切,在现实生产生活中特别是风险决策中有着重要意义.
专题一 离散型随机变量的分布列、均值与方差
类型一 离散型随机变量的分布列、均值和方差
袋中有4个红球,2个黑球,从中任取3个小球,并记录其颜色.
(1)求取到黑球个数X1的均值与方差;
(2)若每次取出1个球后放回,连续取3次,求取到黑球个数X2的均值与方差;
(3)在(2)的基础上,取出1个黑球计2分,取出白球不得分,求所得分数Y的均值与方差.
【例1】
专题二 条件概率
在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
解 设“第1次抽到理科题”为事件A,“第2次抽到理科题”为事件B,则“第1次和第2次都抽到理科题”为事件AB.
【例2】
类型二 条件概率的求法
求相互独立事件一般与互斥事件、对立事件结合在一起进行考查,解答此类问题时应分清事件间的内部联系,在些基础上用基本事件之间的交、并、补运算表示出有关事件,并运用相应公式求解.
特别注意以下两公式的使用前提
(1)若A,B互斥,则P(A∪B)=P(A)+P(B),反之不成立.
(2)若A,B相互独立,则P(AB)=P(A)P(B),反之成立.
专题三 相互独立事件的概率
1.
2.
类型三 求相互独立事件的概率
在某次1500米体能测试中,甲、乙、丙三人各自通过测试的概率分别为 ,求:
(1)3人都通过体能测试的概率;
(2)恰有2人通过体能测试的概率.
【例3】
解 设A表示事件“甲通过体能测试”,
B表示事件“乙通过体能测试”,
C表示事件“丙通过体能测试”.
(1)设M1表示事件“甲、乙、丙3人都通过体能测试”,
即M1=ABC.
由事件A,B,C相互独立,可得:
(2)设M2表示事件“甲、乙、丙3人中只有2人通过体能测试”,
正态密度曲线恰好关于参数μ对称,因此充分利用该图形的对称性及3个特殊区间内的概率值来求解其他区间的概率值,是一种非常简捷的方式.
专题四 正态分布
某市去年高考考生成绩X服从正态分布N(500,502),现有25 000名考生,试确定考生成绩在550~600分的人数.
【例4】
类型四 正态分布
03 真题放送
(2016.四川高考)同时抛掷两枚质地均匀的硬币,当至少有一枚硬币正面向上时,就说这次实验成功,则在2次试验中成功次数X的均值是______.
