高中数学选修2-3第二章 随机变量及其分布 线性相关与回归分析数学建模实验课课件 20张PPT
文档属性
| 名称 | 高中数学选修2-3第二章 随机变量及其分布 线性相关与回归分析数学建模实验课课件 20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 634.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-02 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
昆明滇池中学数学建模实验课
线性相关与回归分析
(一)相关关系
(1)函数关系: 是事物间的关系是确定性关系.
即:当一个变量x取一定值时,另一变量y可以依确定的关系取一个确定的值.
(2)相关关系:是事物间的关系不是确定性关系.
即:当一个变量x取一定值时,另一变量y的取值可能不确定.一个变量的值不能由另一个变量唯一确定.
复习知识点:
(3)目的
通过样本数据,研究两变量间线性相关程度的强弱
(4)基本方法
绘制散点图、计算相关系数
(二) 相关分析和回归分析的任务
研究对象:相关关系
相关分析旨在测度变量间线性关系的强弱程度.
回归分析侧重考察变量之间的数量变化规律,并通过一定的数学表达式来描述这种关系,进而确定一个或几个变量的变化对另一个变量的影响程度.
(三)回归分析
回归线的获得方式:拟和数学关系式(回归模型)
确定解释变量和预报变量
从样本数据出发确定变量之间的数学关系式,使数据拟合于某条曲线;
利用已知数据在一定的统计准则(最小二乘法)下找出参数的估计值(得到回归曲线的近似);
对回归方程进行各种统计检验(残差分析、拟和优度检验);
利用回归方程进行预测.
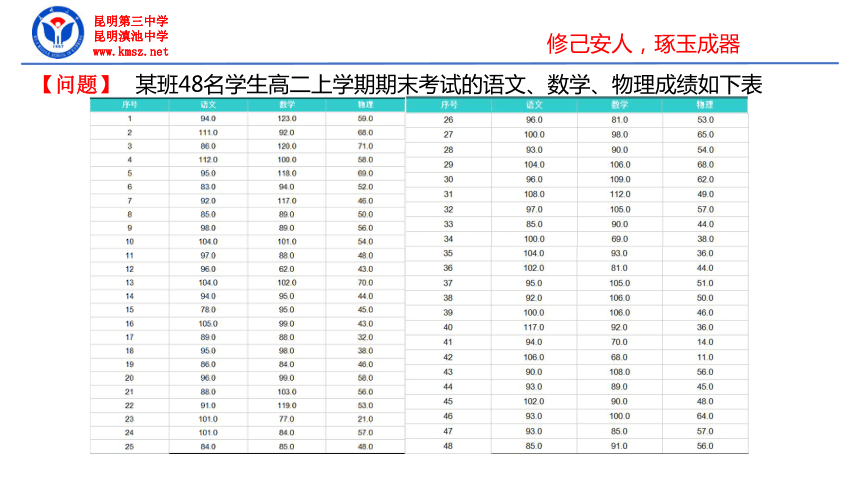
【问题】
某班48名学生高二上学期期末考试的语文、数学、物理成绩如下表
如果把数学成绩和物理成绩看成是两个变量,那么这两个变量之间的关系是什么关系?怎么进行定性定量分析?用什么模型刻画?数学成绩和语文成绩之间的关系又如何呢?
能否由自己的数学成绩预测分析物理学习情况?
小组讨论如何构建模型解决问题?如何进行合理的相关分析和回归分析?
具体分工和实验步骤是哪些?
【实验内容与步骤】
内容1 用随机抽样得到样本数据,用图形计算器TI-nspire cx-c画出散点图,直观分析数学与物理、数学与语文学科之间的相关性。
内容2 分别求出数学与语文、数学与物理之间的相关系数,并分析哪组学科相关性强。构建数学模型。
内容3 求回归直线方程 ,并用图形计算器TI-nspire cx-c画回归直线。
内容4 借助数学、物理的回归直线,用图形计算器TI-nspire cx-c得到回归直线的残差平方和,分析回归直线的合理性。
内容5 借助数学、物理的回归直线,根据自己的数学成绩预测物理成绩。
内容6 是否有其他回归模型?哪一个拟合效果更佳?
内容1 用随机抽样得到样本数据,用图形计算器TI-spire cx-c画出散点图,直观分析数学与物理、数学与语文学科之间的相关性。
【实验内容与步骤】
内容2 分别求出数学与语文、数学与物理之间的相关系数,并分析哪组学科相关性强。
【实验内容与步骤】
【实验内容与步骤】
内容3 求回归直线方程 ,并用图形计算器
TI-nspire cx-c画回归直线。
【实验内容与步骤】
内容4 借助数学、物理的回归直线,用图形计算器
TI-nspire cx-c得到回归直线的残差平方和,分析回归直线的合理性。
内容5 借助数学、物理的回归直线,根据自己的数学成绩预测物理成绩。
【实验内容与步骤】
采用随机抽样,得到如下样本数据:
序号 语文 数学 物理
1 94 123 59
5 95 118 69
9 98 89 56
13 104 102 70
17 89 88 32
21 88 103 56
25 84 85 48
29 104 106 68
33 85 90 44
37 95 105 51
41 94 70 14
45 102 90 48
【实验内容与步骤】
内容6 会用Excel“趋势预测/回归分析”求出拟和优度检验判定系数 ,合理进行回归曲线分析。
数学模型
实验方案步骤
步骤一完成情况 散点图 直观结论
步骤二完成情况 数学与语文的相关系数 数学与物理的相关系数
步骤三完成情况 两种方式求回归直线
步骤四完成情况 残差平方和及回归直线合理性
步骤五完成情况 预测个人物理成绩、分析原因
步骤六完成情况 不同模型 及拟合效果
【实验评价设计】
【实验总结】
进行线性相关与回归分析方案:
散点图→相关性→回归直线方程→回归直线合理性(残差分析)→拟和优度检验→改进模型→预测
【启示与收获】
【课外研究】
请寻找生活中两个变量作一个统计调查,
分析它们的相关性,并提出你的看法或建议。
昆明滇池中学数学建模实验课
线性相关与回归分析
(一)相关关系
(1)函数关系: 是事物间的关系是确定性关系.
即:当一个变量x取一定值时,另一变量y可以依确定的关系取一个确定的值.
(2)相关关系:是事物间的关系不是确定性关系.
即:当一个变量x取一定值时,另一变量y的取值可能不确定.一个变量的值不能由另一个变量唯一确定.
复习知识点:
(3)目的
通过样本数据,研究两变量间线性相关程度的强弱
(4)基本方法
绘制散点图、计算相关系数
(二) 相关分析和回归分析的任务
研究对象:相关关系
相关分析旨在测度变量间线性关系的强弱程度.
回归分析侧重考察变量之间的数量变化规律,并通过一定的数学表达式来描述这种关系,进而确定一个或几个变量的变化对另一个变量的影响程度.
(三)回归分析
回归线的获得方式:拟和数学关系式(回归模型)
确定解释变量和预报变量
从样本数据出发确定变量之间的数学关系式,使数据拟合于某条曲线;
利用已知数据在一定的统计准则(最小二乘法)下找出参数的估计值(得到回归曲线的近似);
对回归方程进行各种统计检验(残差分析、拟和优度检验);
利用回归方程进行预测.
【问题】
某班48名学生高二上学期期末考试的语文、数学、物理成绩如下表
如果把数学成绩和物理成绩看成是两个变量,那么这两个变量之间的关系是什么关系?怎么进行定性定量分析?用什么模型刻画?数学成绩和语文成绩之间的关系又如何呢?
能否由自己的数学成绩预测分析物理学习情况?
小组讨论如何构建模型解决问题?如何进行合理的相关分析和回归分析?
具体分工和实验步骤是哪些?
【实验内容与步骤】
内容1 用随机抽样得到样本数据,用图形计算器TI-nspire cx-c画出散点图,直观分析数学与物理、数学与语文学科之间的相关性。
内容2 分别求出数学与语文、数学与物理之间的相关系数,并分析哪组学科相关性强。构建数学模型。
内容3 求回归直线方程 ,并用图形计算器TI-nspire cx-c画回归直线。
内容4 借助数学、物理的回归直线,用图形计算器TI-nspire cx-c得到回归直线的残差平方和,分析回归直线的合理性。
内容5 借助数学、物理的回归直线,根据自己的数学成绩预测物理成绩。
内容6 是否有其他回归模型?哪一个拟合效果更佳?
内容1 用随机抽样得到样本数据,用图形计算器TI-spire cx-c画出散点图,直观分析数学与物理、数学与语文学科之间的相关性。
【实验内容与步骤】
内容2 分别求出数学与语文、数学与物理之间的相关系数,并分析哪组学科相关性强。
【实验内容与步骤】
【实验内容与步骤】
内容3 求回归直线方程 ,并用图形计算器
TI-nspire cx-c画回归直线。
【实验内容与步骤】
内容4 借助数学、物理的回归直线,用图形计算器
TI-nspire cx-c得到回归直线的残差平方和,分析回归直线的合理性。
内容5 借助数学、物理的回归直线,根据自己的数学成绩预测物理成绩。
【实验内容与步骤】
采用随机抽样,得到如下样本数据:
序号 语文 数学 物理
1 94 123 59
5 95 118 69
9 98 89 56
13 104 102 70
17 89 88 32
21 88 103 56
25 84 85 48
29 104 106 68
33 85 90 44
37 95 105 51
41 94 70 14
45 102 90 48
【实验内容与步骤】
内容6 会用Excel“趋势预测/回归分析”求出拟和优度检验判定系数 ,合理进行回归曲线分析。
数学模型
实验方案步骤
步骤一完成情况 散点图 直观结论
步骤二完成情况 数学与语文的相关系数 数学与物理的相关系数
步骤三完成情况 两种方式求回归直线
步骤四完成情况 残差平方和及回归直线合理性
步骤五完成情况 预测个人物理成绩、分析原因
步骤六完成情况 不同模型 及拟合效果
【实验评价设计】
【实验总结】
进行线性相关与回归分析方案:
散点图→相关性→回归直线方程→回归直线合理性(残差分析)→拟和优度检验→改进模型→预测
【启示与收获】
【课外研究】
请寻找生活中两个变量作一个统计调查,
分析它们的相关性,并提出你的看法或建议。
