高中数学选修2-3第二章 随机变量及其分布 μ,σ对正态分布的影响 课件 29张PPT
文档属性
| 名称 | 高中数学选修2-3第二章 随机变量及其分布 μ,σ对正态分布的影响 课件 29张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 17:18:56 | ||
图片预览






文档简介
(共29张PPT)
课题:2.4正态分布
学科:数学
年级:高二
版本:人教A版选修2-3
亨利·庞加莱 [1] (Jules Henri Poincaré,1854年4月29日—1912年7月17日),法国数学家、天体力学家、数学物理学家、科学哲学家
1.利用实际问题的直方图,了解正态分布曲线的特点及曲线所表示的意义.(重点)
2.了解变量落在区间(μ-σ,μ+σ],
(μ-2σ,μ+2σ],(μ-3σ,μ+3σ]的
概率大小.(重点)
3.会用正态分布去解决实际问题.(难点)
课前预习任务
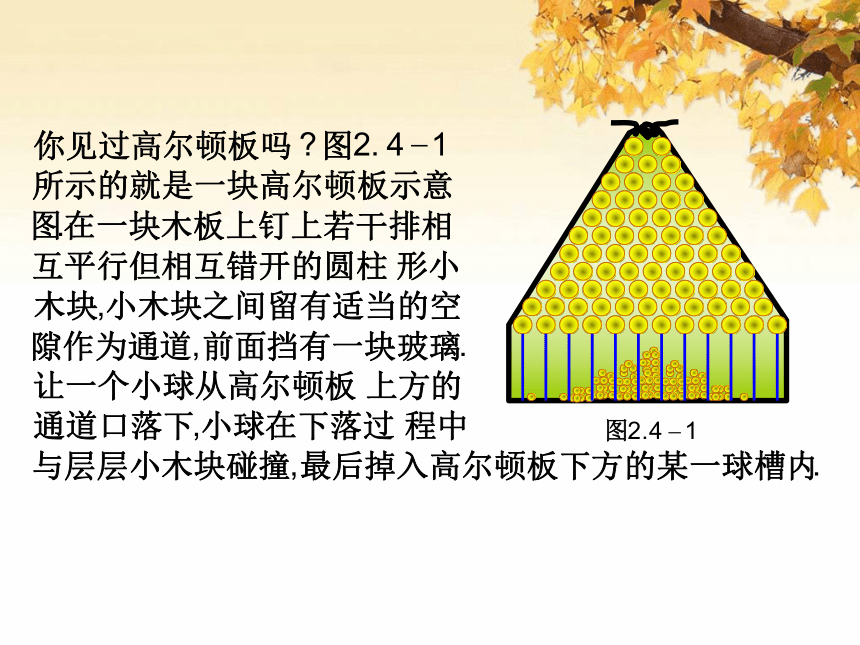
请同学们仔细阅读教材,以小组为单位进行高尔顿钉板试验,并思考以下问题:
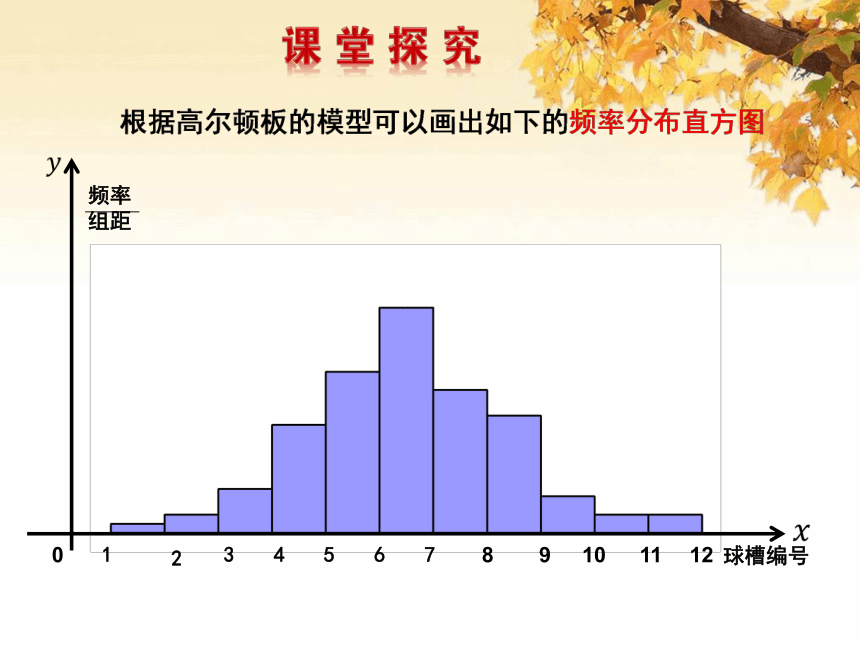
1.试验过程中,小球碰撞和落入的位置,随着试验次数增加,球槽中小球堆积的高度及形状特点?
2.如何用我们所学的知识研究落在各个球槽内的小球的分布情况?
1
2
4
3
5
6
7
频率
组距
8
9
10
11
12
0
球槽编号
频率
组距
球槽编号
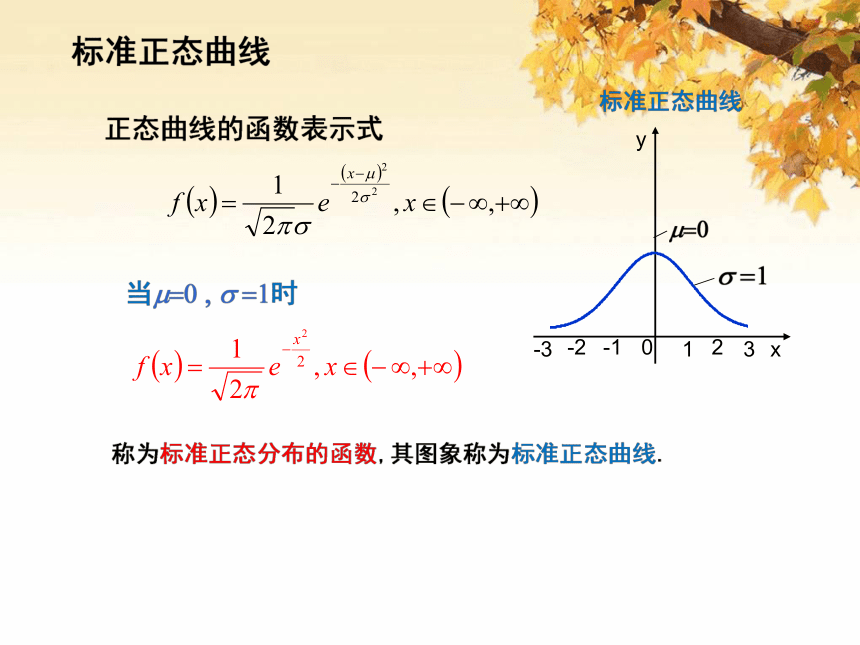
1. 正态曲线的定义
从正态曲线分析,随机变量X在区间(a,b]内取值的概率有什么几何意义?在理论上如何计算?
一般地,如果对于任何实数a,b(a<b),随机
变量X满足 ,则称X的分
布为正态分布,记作X~N( ,σ2).其中 ,σ为
参数.
正态曲线下的面积规律
X轴与正态曲线所夹面积恒等于1 。
对称区域面积相等。
S(-?,-X)
S(X,?)=S(-?,-X)
?
例1: 在一次测试中,测量结果X服从正态分布
N(2,σ2)(σ>0),若X在(0,2)内取值的概率为
0.2,求:
(1)X在(0,4)内取值的概率.
(2)P(X>4).
2. 正态曲线的特点
3. 特殊区间的概率
例2、若X~N(5,1),求P(6解:
1.设两个正态分布N(μ1, )(σ1>0)和N(μ2, )
(σ2>0)的密度函数图象如图所示,则有 ( )
A.μ1<μ2,σ1<σ2
B.μ1<μ2,σ1 > σ2
C.μ1>μ2,σ1<σ2
D.μ1>μ2,σ1>σ2
A
B
我们用一节课的时间认识了正态曲线及其所表示的意义,事实上,从历史上看,正态分布从1733年问世到作为分析统计数据的概率模型经历了100多年,经过棣莫弗、高斯、凯特莱和高尔顿等很多科学家的辛苦努力.课后请同学们查阅相关的资料,了解正态分布的发展史.
哪里有数学,哪里就有美!
课题:2.4正态分布
学科:数学
年级:高二
版本:人教A版选修2-3
亨利·庞加莱 [1] (Jules Henri Poincaré,1854年4月29日—1912年7月17日),法国数学家、天体力学家、数学物理学家、科学哲学家
1.利用实际问题的直方图,了解正态分布曲线的特点及曲线所表示的意义.(重点)
2.了解变量落在区间(μ-σ,μ+σ],
(μ-2σ,μ+2σ],(μ-3σ,μ+3σ]的
概率大小.(重点)
3.会用正态分布去解决实际问题.(难点)
课前预习任务
请同学们仔细阅读教材,以小组为单位进行高尔顿钉板试验,并思考以下问题:
1.试验过程中,小球碰撞和落入的位置,随着试验次数增加,球槽中小球堆积的高度及形状特点?
2.如何用我们所学的知识研究落在各个球槽内的小球的分布情况?
1
2
4
3
5
6
7
频率
组距
8
9
10
11
12
0
球槽编号
频率
组距
球槽编号
1. 正态曲线的定义
从正态曲线分析,随机变量X在区间(a,b]内取值的概率有什么几何意义?在理论上如何计算?
一般地,如果对于任何实数a,b(a<b),随机
变量X满足 ,则称X的分
布为正态分布,记作X~N( ,σ2).其中 ,σ为
参数.
正态曲线下的面积规律
X轴与正态曲线所夹面积恒等于1 。
对称区域面积相等。
S(-?,-X)
S(X,?)=S(-?,-X)
?
例1: 在一次测试中,测量结果X服从正态分布
N(2,σ2)(σ>0),若X在(0,2)内取值的概率为
0.2,求:
(1)X在(0,4)内取值的概率.
(2)P(X>4).
2. 正态曲线的特点
3. 特殊区间的概率
例2、若X~N(5,1),求P(6
1.设两个正态分布N(μ1, )(σ1>0)和N(μ2, )
(σ2>0)的密度函数图象如图所示,则有 ( )
A.μ1<μ2,σ1<σ2
B.μ1<μ2,σ1 > σ2
C.μ1>μ2,σ1<σ2
D.μ1>μ2,σ1>σ2
A
B
我们用一节课的时间认识了正态曲线及其所表示的意义,事实上,从历史上看,正态分布从1733年问世到作为分析统计数据的概率模型经历了100多年,经过棣莫弗、高斯、凯特莱和高尔顿等很多科学家的辛苦努力.课后请同学们查阅相关的资料,了解正态分布的发展史.
哪里有数学,哪里就有美!
