选修2--3的第三章统计案例《统计案例--实习作业》课件 41张PPT
文档属性
| 名称 | 选修2--3的第三章统计案例《统计案例--实习作业》课件 41张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 17:39:20 | ||
图片预览










文档简介
(共41张PPT)
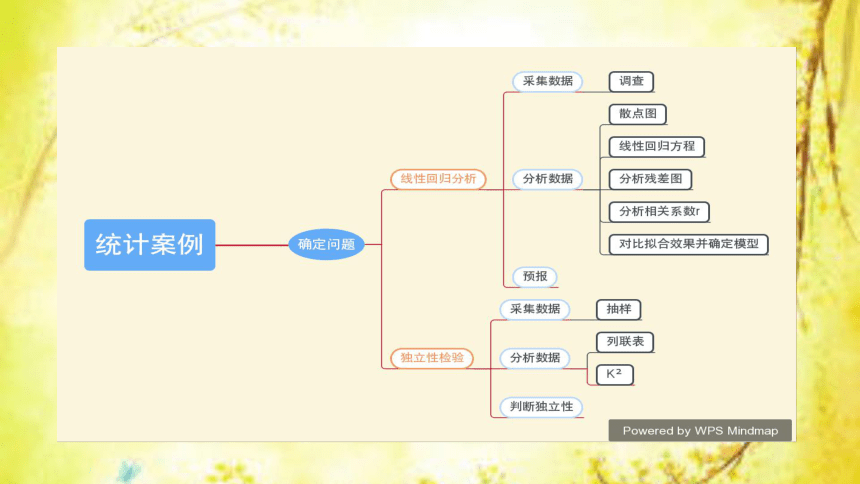
统计案例——实习作业
探究:运动时长与感冒次数之间的关系
第一小组 组长:韩宇轩
小组分工
韩宇轩 统筹/PPT
刘帅 任奕 雒宴徽 设计抽样/设计调查问卷及注意事项
张萱 高昕垚 数据采集
孙移丞 数据分析
李若清 冯露 误差分析
成果分享 应用巩固
确定问题①(小组全体成员)
运动对于提高免疫力有着重要作用,而感冒作为生活中最常见的疾病,其发病与免疫力有着密切的关系。因此,我们对“运动时间是否与感冒次数有关”问题做了研究。
确定问题②(小组全体成员)
需要注意的两条基本原则:
①学校每周规定的运动时间为2h(体育课40min*2、早晨跑操10min*4),:
②感冒与多种因素有关,一年内有不多几次属正常情况或不属于本次研究范围。
因此,我们将问题确定为“每周运动时间是否超过3h与一年内感冒次数是否少于两次之间是否有关”。
设计抽样(刘帅 任奕 雒宴徽)
抽样范围:
本校高二年级2,3,4,7,9,11,13,14班
抽样过程: 2班 31人 3班 33人
7班 29人 9班 22人
11班 31人 13班 23人
14班 21人
(共190人)
数据采集(张萱 高昕垚)
共采集数据190份,其中
每周运动时间3h以上且一年感冒两次以下 64人
每周运动时间3h以下且一年感冒两次以下 51人
每周运动时间3h以上且一年感冒两次以上 36人
每周运动时间3h以下且一年感冒两次以上 39人
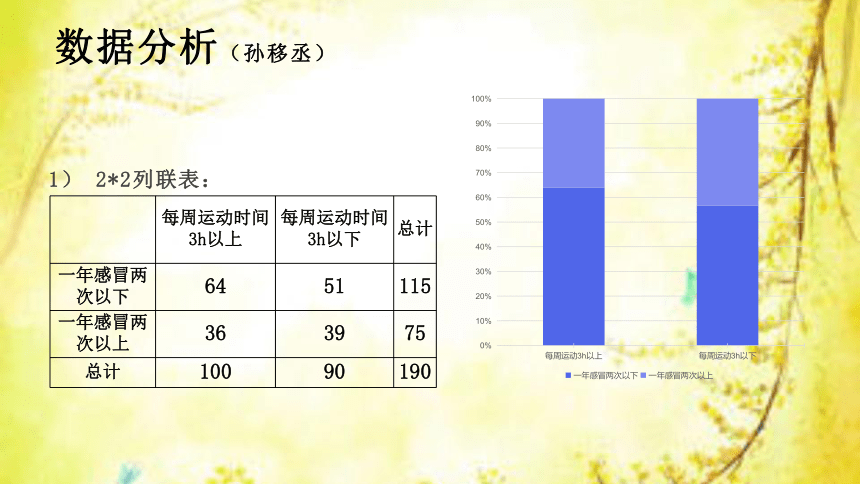
数据分析(孙移丞)
1) 2*2列联表:
每周运动时间3h以上 每周运动时间3h以下 总计
一年感冒两次以下 64 51 115
一年感冒两次以上 36 39 75
总计 100 90 190
2) 计算: k=[190*(64*39-51*36)?]/(100*90*115*75)≈1.06>0.708
∴P(K?≥k0)=0.4
P(K2.≥k0) 0.50 0.40 0.25 0.15 0.10 0.05
k0 0.455 0.708 1.323 2.072 2.706 3.841
综上所述,在错误概率不超过40%的情况下,“感冒的次数”与“运动时间”存在相关关系。
误差分析(李若清 冯露)
1)系统误差:
① 样本容量较小,普遍性不足;
② 13班为文科班,14班为体育班,运动量可能与其他班出入较大;
③ 感冒本身存在多种因素,仅认为与运动量有关是不准确的。
2)人为误差:
① 抽样可能不均匀。
拓展问题
1)将样本容量扩大到本校高二、高三年级,以上误差是否会缩小?
2)实际上使人患感冒的因素有许多种,究竟哪一种与感冒的相关性最强?
3)根据上述调查和拓展问题研究,如何减少患感冒的几率?
4)在本问题中,我们利用独立性检验思想对问题做了研究,但只有60%的把握判定两个变量之间存在相关关系。那么,是否可以换用线性回归思想对“感冒的次数”与“运动时间”进行拟合?
我国GDP与年份之间的关系
第二小组 组长:王琦
成果分享 应用巩固
小组成员
张帆 制作PPT 杨宇博 查找资料
张雨欣 查找资料 孙艺洳 查找资料
王欣雨 查找资料 雒兴荣 分析数据
陈佳怡 分析数据 王琦 误差分析
孙雅琪 误差分析 李子鑫 拓展问题
使用指数函数/二次函数模型拟合:
设y=c1ec2x
lny=lnc1+c2x
令z=lny b=c2 c=lnc1
则有:z=bx+a(a=lnc1,b=c2)
设y=c3x2+c4
即令t=x2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
由拟合模型及数据代入线性回归公式:
可得:b=0.1348
a=-258.0263
即线性回归方程为:z=0.1348x-258.0263
因此该非线性回归方程为:
Y=e0.1348x-258.0263
根据散点图可得线性回归方程为:
Y=2.1214 t-8209417.579
即非线性回归方程为:
Y=2.1214x2-8209417.576
|
|
|
|
|
|
|
|
比较两个回归方程的拟合效果
通过残差来比较两个回归方程的拟合效果:
ei(1)=yi-yi(1)=yi-e0.1348x-258.0263,i=1,2……29
ei(2)=yi-yi(2) =yi-2.1214x2-8209417.576 ,i=1,2……29
由残差公式计算可知:指数函数残差绝对值小于二次函数残差绝对值,即指数函数模型拟合效果要好于二次函数模型拟合效果。
即使用回归方程: Y=e0.1348x-258.0263
对数据的解释
2001年11月10日,在卡塔尔多哈举行的世界贸易组织(WTO)第四届部长级会议通过了中国加入世贸组织法律文件,它标志着经过15年的艰苦努力,我国终于成为世贸组织新成员。
成员分工
李民扬 汇报报告 崔梦琪 收集数据
康泽华 统计数据 王喜泽 统计数据
王旭 制作PPT 计算数据 刘澜浩 制作PPT
钱蕾诗
收集数据
杨文婕 收集数据
21世纪是人类全面进入信息化社会的世纪。伴随网络技术的发展和作为通讯工具手机的普及,手机已逐渐成为中学生的新宠。近几年来,只要你稍加留意,随处可以看到一些中学生拿着手机侃侃而谈。随着中学生使用手机的人数也越来越多,使用的手机也越来越好,对于正处在身心发展的关键时期的学生们来说,使用手机对他们的成长是否有好处?是利大于弊还是弊大于利?手机在校园内的流行,使我们不得不重视这个问题。为此我决定做次调查。
确定问题
通过调查,我们收集了308个人的数据,如下表
不玩手机 玩手机 总计
进步 43 113 156
退步 53 99 152
总计 96 212 308
列联表:
假设退步与玩手机没有关系,即退步与玩手机相互独立。
不玩手机 玩手机 总计
进步 a b a+b
退步 c d c+d
总计 a+c b+d a+b+c+d
所以K2=n(ad-bc)2/(a+b)(c+d)(a+c)(b+d)
=308(4257-5989)2/156*152*96*21
=19.32
因为19.32>10.828 所以玩手机与退步相互独立的概率为0.001
由此看来,玩手机与学习退步还是有很大的联系的
P(K2≥k) 0.5 0.4 0.25 0.15 0.1
k 0.455 0.708 1.323 2.072 2.706
P(K2≥k) 0.05 0.025 0.01 0.005 0.001
k 3.841 5.024 6.635 7.879 10.828
通过以上数据, 同学们不难看出玩手机和学习成绩是有很大关系的。
但为什么有的人玩手机但学习还是进步了呢?是因为他们合理的利用了手机。
其实用手机学习是可以的,但是有的人因此而成绩下降我认为是因为自己的心没有用在学业上,没有控制好玩手机的时间,一门心思只想玩手机,这才导致成绩下降。那么我们该如何正确的利用手机呢?我有以下几点建议
1.我们可以适当的在学累了的时候用手机听听歌来放松以下而不是去玩游戏。
2.在学习上有不懂得地方可以去查以下让自己弄明白而不是去查题,抄作业。
3.合理安排在闲暇时适用手机的时间,不能沉迷进去。
● 当然我们这组数据是有局限性的,因为我们只调查了高二的同学,不可能对所有的同学都适用所以还有以下几个问题同学们可以自己去探讨。
问题与思考
如果这个调查人数变多,那么结果会怎么变化?
退步主要因素是什么?
怎样合理利用手机?
退步和玩手机有线性关系吗?如果有那么其回归方程是什么?
第四小组 组长:王俊宇
探究:文理科与性别之间的关系
成果分享 应用巩固
思维导图
小组成员及分配:
1 设计问卷调查 何生虎、段莹
2 收集数据 王贝,马晓菲
3 分析数据、得出结论 徐冰泓,关钰莹
4 编制报告 苏顺慧、吴诺毅
5 制作PPT 王俊宇、张维文
在高三三班37名同学中进行问卷调查,得到以下列联表及柱状图。
收集数据
理科优势 文科优势 总计
男生 11 7 18
女生 7 10 17
总计 18 17 35
根据列联表中的数据得到:
K2= =1.3908
分析数据
P(K2.≥k0) 0.50 0.40 0.25 0.15 0.10 0.05
k0 0.455 0.708 1.323 2.072 2.706 3.841
P(K2 ≥1.323)≈ 0.25
因此,在犯错误的概率不超过0.25的前提下,认为性别与文理科目优势有关。
即:有75%的把握认为性别与文理科目优势有关。
男生中:理科优势有61.1%;
女生中:理科优势有41.2%
男生较偏理科优势,女生较偏文科优势。
分析数据
影响性别分科差异的因素可能有以下几点:
1、高中阶段科目学习的难易程度确实存在不容忽视的性别因素,男生在逻辑推理计算方面较女生强,而女生在语言学习上比男生有优势。
2、学习成绩和学习投入形成的反馈效应,使得男女生对自己更为擅长的科目形成浓厚的兴趣,投入的时间会更多。
3、社会的重理轻文思想导致了学生和家长对理科的倾向性。
产生以上结果的因素分析
在高中阶段男生选择理科的多,女生选择文科的多,如此更能发挥各自的优势。
结论
总之,在高中阶段谁会更优秀,性别不是决定性因素,适应高强度的学习节奏并持续努力才更为重要!
请同学们对以上的四个问题和分析过程作出评价。
小组讨论 相互评价 提出问题
问题反思(第一小组 韩宇轩)
在第一个问题中,我们运用独立性检验思想对运动时间与感冒次数之间的关系作了分析。那么,能否运用线性回归的知识,从另一方面对这个问题作出分析?
用数学的眼光观察世界
用数学的思维思考世界
用数学的语言表达世界
统计案例——实习作业
探究:运动时长与感冒次数之间的关系
第一小组 组长:韩宇轩
小组分工
韩宇轩 统筹/PPT
刘帅 任奕 雒宴徽 设计抽样/设计调查问卷及注意事项
张萱 高昕垚 数据采集
孙移丞 数据分析
李若清 冯露 误差分析
成果分享 应用巩固
确定问题①(小组全体成员)
运动对于提高免疫力有着重要作用,而感冒作为生活中最常见的疾病,其发病与免疫力有着密切的关系。因此,我们对“运动时间是否与感冒次数有关”问题做了研究。
确定问题②(小组全体成员)
需要注意的两条基本原则:
①学校每周规定的运动时间为2h(体育课40min*2、早晨跑操10min*4),:
②感冒与多种因素有关,一年内有不多几次属正常情况或不属于本次研究范围。
因此,我们将问题确定为“每周运动时间是否超过3h与一年内感冒次数是否少于两次之间是否有关”。
设计抽样(刘帅 任奕 雒宴徽)
抽样范围:
本校高二年级2,3,4,7,9,11,13,14班
抽样过程: 2班 31人 3班 33人
7班 29人 9班 22人
11班 31人 13班 23人
14班 21人
(共190人)
数据采集(张萱 高昕垚)
共采集数据190份,其中
每周运动时间3h以上且一年感冒两次以下 64人
每周运动时间3h以下且一年感冒两次以下 51人
每周运动时间3h以上且一年感冒两次以上 36人
每周运动时间3h以下且一年感冒两次以上 39人
数据分析(孙移丞)
1) 2*2列联表:
每周运动时间3h以上 每周运动时间3h以下 总计
一年感冒两次以下 64 51 115
一年感冒两次以上 36 39 75
总计 100 90 190
2) 计算: k=[190*(64*39-51*36)?]/(100*90*115*75)≈1.06>0.708
∴P(K?≥k0)=0.4
P(K2.≥k0) 0.50 0.40 0.25 0.15 0.10 0.05
k0 0.455 0.708 1.323 2.072 2.706 3.841
综上所述,在错误概率不超过40%的情况下,“感冒的次数”与“运动时间”存在相关关系。
误差分析(李若清 冯露)
1)系统误差:
① 样本容量较小,普遍性不足;
② 13班为文科班,14班为体育班,运动量可能与其他班出入较大;
③ 感冒本身存在多种因素,仅认为与运动量有关是不准确的。
2)人为误差:
① 抽样可能不均匀。
拓展问题
1)将样本容量扩大到本校高二、高三年级,以上误差是否会缩小?
2)实际上使人患感冒的因素有许多种,究竟哪一种与感冒的相关性最强?
3)根据上述调查和拓展问题研究,如何减少患感冒的几率?
4)在本问题中,我们利用独立性检验思想对问题做了研究,但只有60%的把握判定两个变量之间存在相关关系。那么,是否可以换用线性回归思想对“感冒的次数”与“运动时间”进行拟合?
我国GDP与年份之间的关系
第二小组 组长:王琦
成果分享 应用巩固
小组成员
张帆 制作PPT 杨宇博 查找资料
张雨欣 查找资料 孙艺洳 查找资料
王欣雨 查找资料 雒兴荣 分析数据
陈佳怡 分析数据 王琦 误差分析
孙雅琪 误差分析 李子鑫 拓展问题
使用指数函数/二次函数模型拟合:
设y=c1ec2x
lny=lnc1+c2x
令z=lny b=c2 c=lnc1
则有:z=bx+a(a=lnc1,b=c2)
设y=c3x2+c4
即令t=x2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
由拟合模型及数据代入线性回归公式:
可得:b=0.1348
a=-258.0263
即线性回归方程为:z=0.1348x-258.0263
因此该非线性回归方程为:
Y=e0.1348x-258.0263
根据散点图可得线性回归方程为:
Y=2.1214 t-8209417.579
即非线性回归方程为:
Y=2.1214x2-8209417.576
|
|
|
|
|
|
|
|
比较两个回归方程的拟合效果
通过残差来比较两个回归方程的拟合效果:
ei(1)=yi-yi(1)=yi-e0.1348x-258.0263,i=1,2……29
ei(2)=yi-yi(2) =yi-2.1214x2-8209417.576 ,i=1,2……29
由残差公式计算可知:指数函数残差绝对值小于二次函数残差绝对值,即指数函数模型拟合效果要好于二次函数模型拟合效果。
即使用回归方程: Y=e0.1348x-258.0263
对数据的解释
2001年11月10日,在卡塔尔多哈举行的世界贸易组织(WTO)第四届部长级会议通过了中国加入世贸组织法律文件,它标志着经过15年的艰苦努力,我国终于成为世贸组织新成员。
成员分工
李民扬 汇报报告 崔梦琪 收集数据
康泽华 统计数据 王喜泽 统计数据
王旭 制作PPT 计算数据 刘澜浩 制作PPT
钱蕾诗
收集数据
杨文婕 收集数据
21世纪是人类全面进入信息化社会的世纪。伴随网络技术的发展和作为通讯工具手机的普及,手机已逐渐成为中学生的新宠。近几年来,只要你稍加留意,随处可以看到一些中学生拿着手机侃侃而谈。随着中学生使用手机的人数也越来越多,使用的手机也越来越好,对于正处在身心发展的关键时期的学生们来说,使用手机对他们的成长是否有好处?是利大于弊还是弊大于利?手机在校园内的流行,使我们不得不重视这个问题。为此我决定做次调查。
确定问题
通过调查,我们收集了308个人的数据,如下表
不玩手机 玩手机 总计
进步 43 113 156
退步 53 99 152
总计 96 212 308
列联表:
假设退步与玩手机没有关系,即退步与玩手机相互独立。
不玩手机 玩手机 总计
进步 a b a+b
退步 c d c+d
总计 a+c b+d a+b+c+d
所以K2=n(ad-bc)2/(a+b)(c+d)(a+c)(b+d)
=308(4257-5989)2/156*152*96*21
=19.32
因为19.32>10.828 所以玩手机与退步相互独立的概率为0.001
由此看来,玩手机与学习退步还是有很大的联系的
P(K2≥k) 0.5 0.4 0.25 0.15 0.1
k 0.455 0.708 1.323 2.072 2.706
P(K2≥k) 0.05 0.025 0.01 0.005 0.001
k 3.841 5.024 6.635 7.879 10.828
通过以上数据, 同学们不难看出玩手机和学习成绩是有很大关系的。
但为什么有的人玩手机但学习还是进步了呢?是因为他们合理的利用了手机。
其实用手机学习是可以的,但是有的人因此而成绩下降我认为是因为自己的心没有用在学业上,没有控制好玩手机的时间,一门心思只想玩手机,这才导致成绩下降。那么我们该如何正确的利用手机呢?我有以下几点建议
1.我们可以适当的在学累了的时候用手机听听歌来放松以下而不是去玩游戏。
2.在学习上有不懂得地方可以去查以下让自己弄明白而不是去查题,抄作业。
3.合理安排在闲暇时适用手机的时间,不能沉迷进去。
● 当然我们这组数据是有局限性的,因为我们只调查了高二的同学,不可能对所有的同学都适用所以还有以下几个问题同学们可以自己去探讨。
问题与思考
如果这个调查人数变多,那么结果会怎么变化?
退步主要因素是什么?
怎样合理利用手机?
退步和玩手机有线性关系吗?如果有那么其回归方程是什么?
第四小组 组长:王俊宇
探究:文理科与性别之间的关系
成果分享 应用巩固
思维导图
小组成员及分配:
1 设计问卷调查 何生虎、段莹
2 收集数据 王贝,马晓菲
3 分析数据、得出结论 徐冰泓,关钰莹
4 编制报告 苏顺慧、吴诺毅
5 制作PPT 王俊宇、张维文
在高三三班37名同学中进行问卷调查,得到以下列联表及柱状图。
收集数据
理科优势 文科优势 总计
男生 11 7 18
女生 7 10 17
总计 18 17 35
根据列联表中的数据得到:
K2= =1.3908
分析数据
P(K2.≥k0) 0.50 0.40 0.25 0.15 0.10 0.05
k0 0.455 0.708 1.323 2.072 2.706 3.841
P(K2 ≥1.323)≈ 0.25
因此,在犯错误的概率不超过0.25的前提下,认为性别与文理科目优势有关。
即:有75%的把握认为性别与文理科目优势有关。
男生中:理科优势有61.1%;
女生中:理科优势有41.2%
男生较偏理科优势,女生较偏文科优势。
分析数据
影响性别分科差异的因素可能有以下几点:
1、高中阶段科目学习的难易程度确实存在不容忽视的性别因素,男生在逻辑推理计算方面较女生强,而女生在语言学习上比男生有优势。
2、学习成绩和学习投入形成的反馈效应,使得男女生对自己更为擅长的科目形成浓厚的兴趣,投入的时间会更多。
3、社会的重理轻文思想导致了学生和家长对理科的倾向性。
产生以上结果的因素分析
在高中阶段男生选择理科的多,女生选择文科的多,如此更能发挥各自的优势。
结论
总之,在高中阶段谁会更优秀,性别不是决定性因素,适应高强度的学习节奏并持续努力才更为重要!
请同学们对以上的四个问题和分析过程作出评价。
小组讨论 相互评价 提出问题
问题反思(第一小组 韩宇轩)
在第一个问题中,我们运用独立性检验思想对运动时间与感冒次数之间的关系作了分析。那么,能否运用线性回归的知识,从另一方面对这个问题作出分析?
用数学的眼光观察世界
用数学的思维思考世界
用数学的语言表达世界
