高中数学人教新课标A版选修3-1第三讲 中国古代数学瑰宝四 中国古代数学家 课件 23张PPT
文档属性
| 名称 | 高中数学人教新课标A版选修3-1第三讲 中国古代数学瑰宝四 中国古代数学家 课件 23张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
一场跨越一千多年的数学文化探索之旅
中国古代数学家
普通高中课程标准试验教科书 . 数学选修3-1
刘徽,中国古代数学理论的奠基人,撰写了世界数学经典名著《九章算术注》.
他的主要贡献有:创造了“割圆术”,运用朴素的极限思想计算圆面积及圆周率;建立了重差术;重视逻辑推理,同时又注意几何直观的作用.
刘徽的重要贡献
刘徽(魏晋年间人)
他是继希腊泰勒斯后,世界论证数学的杰出代表之一.
刘徽的“割圆术”
《九章算术》中关于圆面积的求法采用的是古法的“周三径一”,这是不够精确的.
刘徽在方田章的“圆田术”中用割圆术计算圆周率,开创了中国数学发展史上圆周率研究的新纪元.
《九章算术》“方田”章:
半周半径相乘得积步,周径相乘,四而一
割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.
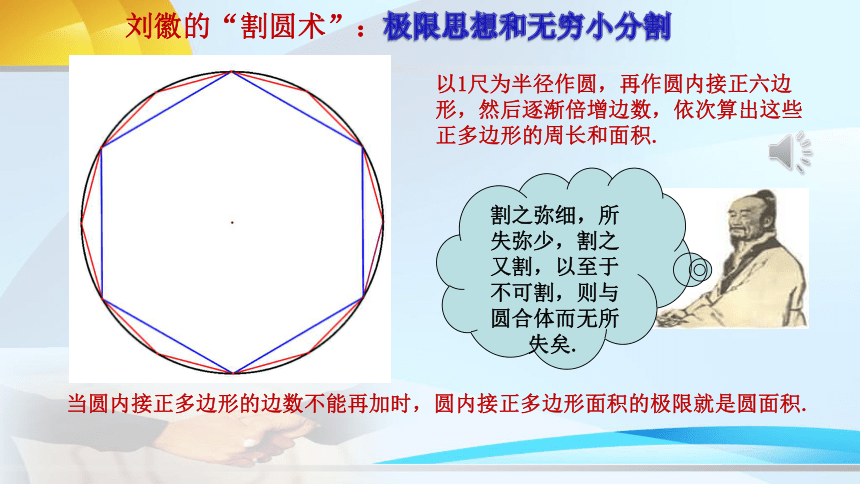
以1尺为半径作圆,再作圆内接正六边形,然后逐渐倍增边数,依次算出这些正多边形的周长和面积.
当圆内接正多边形的边数不能再加时,圆内接正多边形面积的极限就是圆面积.
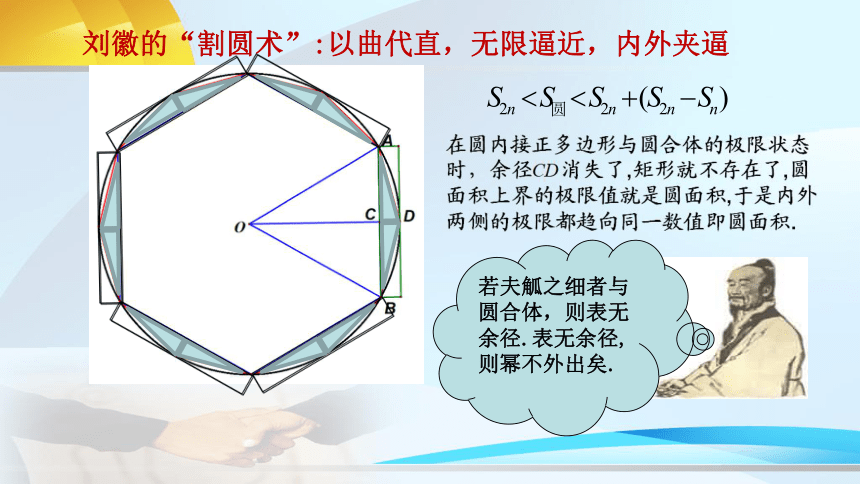
刘徽的“割圆术”:以曲代直,无限逼近,内外夹逼
若夫觚之细者与圆合体,则表无余径.表无余径,则幂不外出矣.
动手试一试
2.598075
3
3.105828
3.132624
3.139344
3.141024
设圆的半径为1,用圆内接正n边形的面积作为圆面积的近似值,估算圆周率.
西方:古希腊的穷竭法
古希腊的科学泰斗阿基米德发明的穷竭法与古代中国的割圆术极相似.根据记载,阿基米德也曾研究过求解圆周率的问题,他是通过圆内接正多边形和圆外切正多边形从正六边形开始加倍的进行,双向逼近圆.
中国古代:刘徽的割圆术
刘徽的割圆术虽然比古希腊晚几百年,但他独辟蹊径,利用已有的结果来表示圆面积的上限,巧妙避开了对圆外切正多边形的计算,在计算圆面积的过程中收到了事半功倍的效果,刘徽割圆术的完备性与数学研究过程中所要求的严密性相符.
建立微积分的先驱人物阿基米德和刘徽
刘徽曰:
然此意非也。何以验之?取立方棋八枚,皆令立方一寸,积之为立方二寸,规之为圆囷,径二寸,高二寸,又复横圆之,则其形有似牟合方盖矣.
刘徽论体积
《九章算术》的《少广》章“开立圆术” :
置积尺数,以十六乘之,九而一,所得开立方除之,即丸径.
牟合方盖
牟合方盖
问题1:正方体的内切球与它的两个内切圆柱是什么关系?
问题2:正方体的内切球与牟合方盖是什么关系?
牟合方盖包含正方体的内切球,并与它相切.
两个圆柱都包含正方体的内切球,并与它相切.
问题3:用一个水平面去截牟合方盖和它的内切球,它们的截面是什么形状?具有怎样的位置关系?
截面为正方形和它的内切圆.
刘徽用截面法研究牟合方盖
问题4:截面圆与其外切正方形的面积之比为多少?
问题5:牟合方盖的内切球与牟合方盖的体积之比为多少?
刘徽论体积
如何计算牟合方盖的体积呢
刘徽:
观立方之内,合盖之外,虽衰杀有渐,而多少不掩,判合总结,方圆相缠,浓纤诡互,不可等正。欲陋形措意,惧失正理. 敢不阙疑,以俟能言者.
祖冲之的“祖率”是一项史无前例的创举
祖冲之(429--500)
中国南北朝时期杰出的数学家、天文学家和机械制造专家.
祖冲之更开密法,以圆径一亿为丈,圆周盈数三丈一尺四寸一分五厘九毫二秒七忽,朒数三丈一尺四寸一分五厘九毫二秒六忽,正数在盈朒二限之间。密率,圆径一百一十三,圆周三百五十五。约率,圆径七,周二十二。
-- 《隋书·律历志》
圆周率数值的上下限:
欲陋形措意,惧失正理.敢不阙疑,以俟能言者
祖暅,祖冲之的儿子
杰出的数学家和天文学家,修补、编辑了祖冲之的《缀术》
这个正确结果记载在《九章算术》“开立圆术”之李淳风注中,称为“祖暅之开立圆术”.
曾经困扰刘徽的球体积问题到祖冲之时代获得了突破。
观立方之内,合盖之外
先取牟合方盖的八分之一及它的外切正方体
祖暅之开立圆术的分解
观立方之内,合盖之外
牟合方盖八分之一及它的外切正方体,再把这个正方体又分出三个小立体,牟合方盖的八分之一部分称为“内棋”,三个小立体称为“外棋”.
祖暅之开立圆术的分解
牟合方盖八分之一及它的外切正方体,再把这个正方体又分出三个小立体,牟合方盖的八分之一部分称为“内棋”,三个小立体称为“外棋”.
祖暅之开立圆术的分解
外三棋
内棋
祖氏原理:幂势既同,则积不容异
高
面积
夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。
祖氏原理在西方称为“卡瓦列利原理”
祖暅之开立圆术的分解
问题1:内棋的截面面积为多少?
问题2:外三棋的截面面积为多少?
问题3:外三棋截面面积的数值可以看成哪个常见平面图形的面积?
由此你能联想学过的哪个几何体的截面正好是这个平面图形?
O
S
N
P
M
可以看成正方形的面积,联想到倒立的正四棱锥,它的截面正好也是正方形
祖暅之开立圆术的分解
问题4:外三棋的体积是多少?
问题5:八分之一牟合方盖的体积是多少?牟合方盖的内切球体积是多少?
1994年哈佛大学主编的《微积分》收录该方法
课堂小结
1.极限思想和微积分思想 2.转化思想 3. 构造法思想
2.从中国古代数学家们的身上我们应该继承和学习他们的哪些精神呢?
1. 富于批判精神
2.注意寻求数学内部的联系
3.注意把数学的逻辑性和直观性结合起来
思想方法:
1.通过本节课的学习,你有哪些收获?
数学史料:
1.圆周率的发展历程 2.球体体积公式的推证过程
3.认识了牟合方盖及其体积公式
课后作业:
1.查阅与刘徽割圆术相关的资料和视频,了解刘徽计算圆内接正n边形面积的方法。
2.找一找生活中还有哪些牟合方盖的实物,并计算它的体积。
优秀传统文化是中华民族的根与魂!
弘扬中华优秀传统文化,
坚定文化自信,
铸就中华文化新辉煌!
一场跨越一千多年的数学文化探索之旅
中国古代数学家
普通高中课程标准试验教科书 . 数学选修3-1
刘徽,中国古代数学理论的奠基人,撰写了世界数学经典名著《九章算术注》.
他的主要贡献有:创造了“割圆术”,运用朴素的极限思想计算圆面积及圆周率;建立了重差术;重视逻辑推理,同时又注意几何直观的作用.
刘徽的重要贡献
刘徽(魏晋年间人)
他是继希腊泰勒斯后,世界论证数学的杰出代表之一.
刘徽的“割圆术”
《九章算术》中关于圆面积的求法采用的是古法的“周三径一”,这是不够精确的.
刘徽在方田章的“圆田术”中用割圆术计算圆周率,开创了中国数学发展史上圆周率研究的新纪元.
《九章算术》“方田”章:
半周半径相乘得积步,周径相乘,四而一
割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.
以1尺为半径作圆,再作圆内接正六边形,然后逐渐倍增边数,依次算出这些正多边形的周长和面积.
当圆内接正多边形的边数不能再加时,圆内接正多边形面积的极限就是圆面积.
刘徽的“割圆术”:以曲代直,无限逼近,内外夹逼
若夫觚之细者与圆合体,则表无余径.表无余径,则幂不外出矣.
动手试一试
2.598075
3
3.105828
3.132624
3.139344
3.141024
设圆的半径为1,用圆内接正n边形的面积作为圆面积的近似值,估算圆周率.
西方:古希腊的穷竭法
古希腊的科学泰斗阿基米德发明的穷竭法与古代中国的割圆术极相似.根据记载,阿基米德也曾研究过求解圆周率的问题,他是通过圆内接正多边形和圆外切正多边形从正六边形开始加倍的进行,双向逼近圆.
中国古代:刘徽的割圆术
刘徽的割圆术虽然比古希腊晚几百年,但他独辟蹊径,利用已有的结果来表示圆面积的上限,巧妙避开了对圆外切正多边形的计算,在计算圆面积的过程中收到了事半功倍的效果,刘徽割圆术的完备性与数学研究过程中所要求的严密性相符.
建立微积分的先驱人物阿基米德和刘徽
刘徽曰:
然此意非也。何以验之?取立方棋八枚,皆令立方一寸,积之为立方二寸,规之为圆囷,径二寸,高二寸,又复横圆之,则其形有似牟合方盖矣.
刘徽论体积
《九章算术》的《少广》章“开立圆术” :
置积尺数,以十六乘之,九而一,所得开立方除之,即丸径.
牟合方盖
牟合方盖
问题1:正方体的内切球与它的两个内切圆柱是什么关系?
问题2:正方体的内切球与牟合方盖是什么关系?
牟合方盖包含正方体的内切球,并与它相切.
两个圆柱都包含正方体的内切球,并与它相切.
问题3:用一个水平面去截牟合方盖和它的内切球,它们的截面是什么形状?具有怎样的位置关系?
截面为正方形和它的内切圆.
刘徽用截面法研究牟合方盖
问题4:截面圆与其外切正方形的面积之比为多少?
问题5:牟合方盖的内切球与牟合方盖的体积之比为多少?
刘徽论体积
如何计算牟合方盖的体积呢
刘徽:
观立方之内,合盖之外,虽衰杀有渐,而多少不掩,判合总结,方圆相缠,浓纤诡互,不可等正。欲陋形措意,惧失正理. 敢不阙疑,以俟能言者.
祖冲之的“祖率”是一项史无前例的创举
祖冲之(429--500)
中国南北朝时期杰出的数学家、天文学家和机械制造专家.
祖冲之更开密法,以圆径一亿为丈,圆周盈数三丈一尺四寸一分五厘九毫二秒七忽,朒数三丈一尺四寸一分五厘九毫二秒六忽,正数在盈朒二限之间。密率,圆径一百一十三,圆周三百五十五。约率,圆径七,周二十二。
-- 《隋书·律历志》
圆周率数值的上下限:
欲陋形措意,惧失正理.敢不阙疑,以俟能言者
祖暅,祖冲之的儿子
杰出的数学家和天文学家,修补、编辑了祖冲之的《缀术》
这个正确结果记载在《九章算术》“开立圆术”之李淳风注中,称为“祖暅之开立圆术”.
曾经困扰刘徽的球体积问题到祖冲之时代获得了突破。
观立方之内,合盖之外
先取牟合方盖的八分之一及它的外切正方体
祖暅之开立圆术的分解
观立方之内,合盖之外
牟合方盖八分之一及它的外切正方体,再把这个正方体又分出三个小立体,牟合方盖的八分之一部分称为“内棋”,三个小立体称为“外棋”.
祖暅之开立圆术的分解
牟合方盖八分之一及它的外切正方体,再把这个正方体又分出三个小立体,牟合方盖的八分之一部分称为“内棋”,三个小立体称为“外棋”.
祖暅之开立圆术的分解
外三棋
内棋
祖氏原理:幂势既同,则积不容异
高
面积
夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。
祖氏原理在西方称为“卡瓦列利原理”
祖暅之开立圆术的分解
问题1:内棋的截面面积为多少?
问题2:外三棋的截面面积为多少?
问题3:外三棋截面面积的数值可以看成哪个常见平面图形的面积?
由此你能联想学过的哪个几何体的截面正好是这个平面图形?
O
S
N
P
M
可以看成正方形的面积,联想到倒立的正四棱锥,它的截面正好也是正方形
祖暅之开立圆术的分解
问题4:外三棋的体积是多少?
问题5:八分之一牟合方盖的体积是多少?牟合方盖的内切球体积是多少?
1994年哈佛大学主编的《微积分》收录该方法
课堂小结
1.极限思想和微积分思想 2.转化思想 3. 构造法思想
2.从中国古代数学家们的身上我们应该继承和学习他们的哪些精神呢?
1. 富于批判精神
2.注意寻求数学内部的联系
3.注意把数学的逻辑性和直观性结合起来
思想方法:
1.通过本节课的学习,你有哪些收获?
数学史料:
1.圆周率的发展历程 2.球体体积公式的推证过程
3.认识了牟合方盖及其体积公式
课后作业:
1.查阅与刘徽割圆术相关的资料和视频,了解刘徽计算圆内接正n边形面积的方法。
2.找一找生活中还有哪些牟合方盖的实物,并计算它的体积。
优秀传统文化是中华民族的根与魂!
弘扬中华优秀传统文化,
坚定文化自信,
铸就中华文化新辉煌!
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
