人教版九年级上册数学第25章《概率初步》单元测试(有答案)
文档属性
| 名称 | 人教版九年级上册数学第25章《概率初步》单元测试(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 157.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-01 11:27:12 | ||
图片预览

文档简介
概率初步
一、单选题
1.在元旦联欢会上,3名小朋友分别站在△ABC三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先做到凳子上谁获胜,为使游戏公平,则凳子应放置的最适当的位置时在△ABC的( )
A.三边中线的交点 B.三条角平分线的交点
C.三边垂直平分线的交点 D.三边上高的交点
2.将一颗骰子(正方体)连掷两次,得到的点数都是4的概率是( )
A. B. C. D.
3.下表记录了一名球员在罚球线上投篮的结果,那么这名球员投篮一次,投中的概率约是( )
投篮次数(n) 50 100 150 200 250 300 500
投中次数(m) 28 60 78 104 123 152 251
投中频率() 0.56 0.60 0.52 0.52 0.49 0.51 0.50
A.0.8 B.0.7 C.0.6 D.0.5
4.下列说法正确的是( )
A.“明天降雨的概率是50%”表示明天有半天都在降雨
B.数据4,3,5,5,0的中位数和众数都是5
C.要了解一批钢化玻璃的最少允许碎片数,应采用普查的方式
D.若甲、乙两组数中各有20个数据,平均数=10,方差s2甲=1.25,s2乙=0.96,则说明乙组数据比甲组数据稳定
5.有四条线段,长度分别是4,6,8,10,从中任取三条能构成直角三角形的概率是( )
A. B. C. D.
6.下列说法正确的是 ( )
A.要了解人们对“低碳生活”的了解程度,宜采用普查方式
B.一组数据5,5,6,7的众数和中位数都是5
C.必然事件发生的概率为100%
D.若甲组数据的方差是3.4,乙组数据的方差是1.68,则甲组数据比乙组数据稳定
7.某校举行春季运动会,需要在七年级选取一名志愿者.七()班、七()班、七()班各有名同学报名参加,现从这名同学中随机选取一名志愿者,则被选中的这名同学恰好是七()班同学的概率是( )
A. B. C. D.
8.一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都随机选择一条路径,并且选择每条路径的可能性相等,则它获得食物的概率是( )
A. B. C. D.
9.有一则笑话:妈妈正在给一对双胞胎洗澡,先洗哥哥,再洗弟弟.刚把两人洗完,就听到两个小家伙在床上笑.“你们笑什么?”妈妈问.“妈妈!”老大回答,“您给弟弟洗了两回,可是还没给我洗呢!”此事件发生的概率为
A. B. C. D.1
10.某小组做“用频率估计概率”的试验时,统计了某结果出现的频率,绘制了如图的折线统计图,则符合这一结果的试验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌花色是红桃
C.袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的面点数是偶数
11.在一个袋子中装有4个黑球和若干个白球,每个球除颜色外都相同,摇匀后从中随机摸出一个球记下颜色,再把它放回袋子中,不断重复上述过程.一共摸了40次,其中有10次摸到黑球,则估计袋子中白球的个数大约是( )
A.12 B.16 C.20 D.30
12.某商店举办有奖储蓄活动,购货满100元者发兑奖券一张,在10000张奖券中,设特等奖1个,一等奖10个,二等奖100个.若某人购物满100元,那么他中一等奖的概率是(?? )
A. B. C. D.
二、填空题
13.已知长度为的四条线段,从中任取三条线段能组成三角形的概率是________.
14.在某校运动会4×400m接力赛中,甲乙两名同学都是第一棒,他们随机从三个赛道中抽取两个不同赛道,则甲乙两名同学恰好抽中相邻赛道的概率为_____.
15.抛掷一枚均匀的硬币,前次都正面朝上,则抛掷第次正面朝上的概率是__________.
16.在不透明的口袋中有若干个完全一样的红色小球,现放入10个仅颜色不同的白色小球,均匀混合后,有放回的随机摸取30次,有10次摸到白色小球,据此估计该口袋中原有红色小球个数为_____.
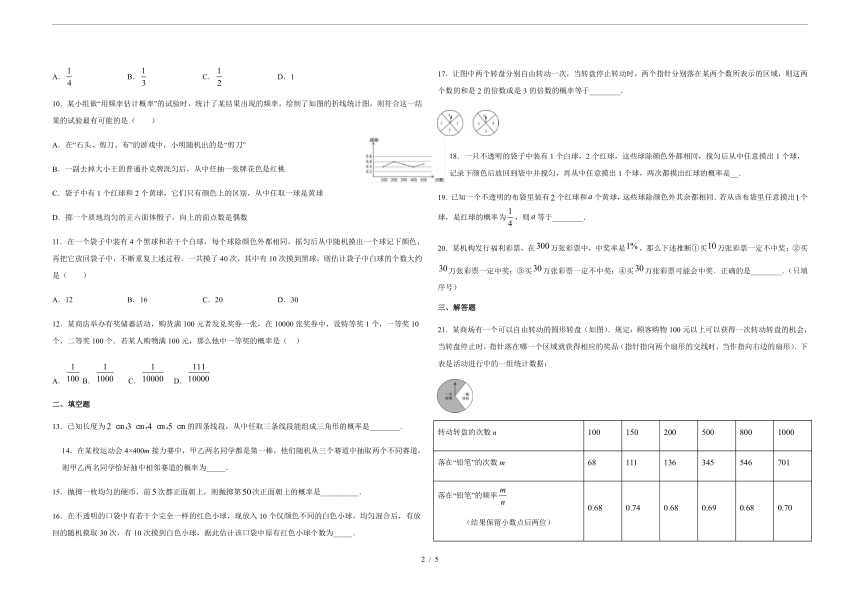
17.让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和是2的倍数或是3的倍数的概率等于________.
18.一只不透明的袋子中装有1个白球,2个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,记录下颜色后放回到袋中并搅匀,再从中任意摸出1个球,两次都摸出红球的概率是__.
19.已知一个不透明的布袋里装有个红球和个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出个球,是红球的概率为,则等于________.
20.某机构发行福利彩票,在万张彩票中,中奖率是,那么下述推断①买万张彩票一定不中奖;②买万张彩票一定中奖;③买万张彩票一定不中奖;④买万张彩票可能会中奖.正确的是________.(只填序号)
三、解答题
21.某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
转动转盘的次数n 100 150 200 500 800 1000
落在“铅笔”的次数m 68 111 136 345 546 701
落在“铅笔”的频率 (结果保留小数点后两位) 0.68 0.74 0.68 0.69 0.68 0.70
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.
22.游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由.
23.口袋A中有2个相同的小球,分别写有数字3,6,口袋B中有4个相同的小球,分别写有数字3,4,5,6,在口袋B中随机地抽出一个小球放入口袋A中.求以口袋A中的3个小球上的数字为边能构成等腰三角形的可能性大小.
24.在4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,不放回,再随机抽取1件进行检测.请用列表法或画树状图的方法,求两次抽到的都是合格品的概率.(解答时可用A表示1件不合格品,用B、C.D分别表示3件合格品)?
(2)在这4件产品中加入若干件合格品后,进行如下试验:随机抽取1件进行检侧,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出大约加入多少件合格品?
25.张华和李明两人玩“剪刀、石头、布”的游戏,游戏规则为:剪刀胜布,布胜石头,石头胜剪刀.
(1)请用列表法或树状图表示出所有可能出现的游戏结果;
(2)求张华胜出的概率.
小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
参考答案
1.C
2.D
3.D
4.D
5.B
6.C
7.B
8.A
9.A
10.D
11.A
12.B
13.
14.
15.
16.20
17.
18.
19.
20.④
21.(1)0.7;(2)该商场每天大致需要支出的奖品费用为5000元;(3)36
22.将转盘A平均分成10分,一份是蓝色,一份是红色,其他是绿色.说明理由见解析
23.
24.(1);(2) 16
25.(1)总共有9种等可能结果.(2).
26.这个游戏对双方不公平,理由略
/
一、单选题
1.在元旦联欢会上,3名小朋友分别站在△ABC三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先做到凳子上谁获胜,为使游戏公平,则凳子应放置的最适当的位置时在△ABC的( )
A.三边中线的交点 B.三条角平分线的交点
C.三边垂直平分线的交点 D.三边上高的交点
2.将一颗骰子(正方体)连掷两次,得到的点数都是4的概率是( )
A. B. C. D.
3.下表记录了一名球员在罚球线上投篮的结果,那么这名球员投篮一次,投中的概率约是( )
投篮次数(n) 50 100 150 200 250 300 500
投中次数(m) 28 60 78 104 123 152 251
投中频率() 0.56 0.60 0.52 0.52 0.49 0.51 0.50
A.0.8 B.0.7 C.0.6 D.0.5
4.下列说法正确的是( )
A.“明天降雨的概率是50%”表示明天有半天都在降雨
B.数据4,3,5,5,0的中位数和众数都是5
C.要了解一批钢化玻璃的最少允许碎片数,应采用普查的方式
D.若甲、乙两组数中各有20个数据,平均数=10,方差s2甲=1.25,s2乙=0.96,则说明乙组数据比甲组数据稳定
5.有四条线段,长度分别是4,6,8,10,从中任取三条能构成直角三角形的概率是( )
A. B. C. D.
6.下列说法正确的是 ( )
A.要了解人们对“低碳生活”的了解程度,宜采用普查方式
B.一组数据5,5,6,7的众数和中位数都是5
C.必然事件发生的概率为100%
D.若甲组数据的方差是3.4,乙组数据的方差是1.68,则甲组数据比乙组数据稳定
7.某校举行春季运动会,需要在七年级选取一名志愿者.七()班、七()班、七()班各有名同学报名参加,现从这名同学中随机选取一名志愿者,则被选中的这名同学恰好是七()班同学的概率是( )
A. B. C. D.
8.一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都随机选择一条路径,并且选择每条路径的可能性相等,则它获得食物的概率是( )
A. B. C. D.
9.有一则笑话:妈妈正在给一对双胞胎洗澡,先洗哥哥,再洗弟弟.刚把两人洗完,就听到两个小家伙在床上笑.“你们笑什么?”妈妈问.“妈妈!”老大回答,“您给弟弟洗了两回,可是还没给我洗呢!”此事件发生的概率为
A. B. C. D.1
10.某小组做“用频率估计概率”的试验时,统计了某结果出现的频率,绘制了如图的折线统计图,则符合这一结果的试验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌花色是红桃
C.袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的面点数是偶数
11.在一个袋子中装有4个黑球和若干个白球,每个球除颜色外都相同,摇匀后从中随机摸出一个球记下颜色,再把它放回袋子中,不断重复上述过程.一共摸了40次,其中有10次摸到黑球,则估计袋子中白球的个数大约是( )
A.12 B.16 C.20 D.30
12.某商店举办有奖储蓄活动,购货满100元者发兑奖券一张,在10000张奖券中,设特等奖1个,一等奖10个,二等奖100个.若某人购物满100元,那么他中一等奖的概率是(?? )
A. B. C. D.
二、填空题
13.已知长度为的四条线段,从中任取三条线段能组成三角形的概率是________.
14.在某校运动会4×400m接力赛中,甲乙两名同学都是第一棒,他们随机从三个赛道中抽取两个不同赛道,则甲乙两名同学恰好抽中相邻赛道的概率为_____.
15.抛掷一枚均匀的硬币,前次都正面朝上,则抛掷第次正面朝上的概率是__________.
16.在不透明的口袋中有若干个完全一样的红色小球,现放入10个仅颜色不同的白色小球,均匀混合后,有放回的随机摸取30次,有10次摸到白色小球,据此估计该口袋中原有红色小球个数为_____.
17.让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和是2的倍数或是3的倍数的概率等于________.
18.一只不透明的袋子中装有1个白球,2个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,记录下颜色后放回到袋中并搅匀,再从中任意摸出1个球,两次都摸出红球的概率是__.
19.已知一个不透明的布袋里装有个红球和个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出个球,是红球的概率为,则等于________.
20.某机构发行福利彩票,在万张彩票中,中奖率是,那么下述推断①买万张彩票一定不中奖;②买万张彩票一定中奖;③买万张彩票一定不中奖;④买万张彩票可能会中奖.正确的是________.(只填序号)
三、解答题
21.某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
转动转盘的次数n 100 150 200 500 800 1000
落在“铅笔”的次数m 68 111 136 345 546 701
落在“铅笔”的频率 (结果保留小数点后两位) 0.68 0.74 0.68 0.69 0.68 0.70
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.
22.游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由.
23.口袋A中有2个相同的小球,分别写有数字3,6,口袋B中有4个相同的小球,分别写有数字3,4,5,6,在口袋B中随机地抽出一个小球放入口袋A中.求以口袋A中的3个小球上的数字为边能构成等腰三角形的可能性大小.
24.在4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,不放回,再随机抽取1件进行检测.请用列表法或画树状图的方法,求两次抽到的都是合格品的概率.(解答时可用A表示1件不合格品,用B、C.D分别表示3件合格品)?
(2)在这4件产品中加入若干件合格品后,进行如下试验:随机抽取1件进行检侧,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出大约加入多少件合格品?
25.张华和李明两人玩“剪刀、石头、布”的游戏,游戏规则为:剪刀胜布,布胜石头,石头胜剪刀.
(1)请用列表法或树状图表示出所有可能出现的游戏结果;
(2)求张华胜出的概率.
小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
参考答案
1.C
2.D
3.D
4.D
5.B
6.C
7.B
8.A
9.A
10.D
11.A
12.B
13.
14.
15.
16.20
17.
18.
19.
20.④
21.(1)0.7;(2)该商场每天大致需要支出的奖品费用为5000元;(3)36
22.将转盘A平均分成10分,一份是蓝色,一份是红色,其他是绿色.说明理由见解析
23.
24.(1);(2) 16
25.(1)总共有9种等可能结果.(2).
26.这个游戏对双方不公平,理由略
/
同课章节目录
