人教版九年级数学上册24.2.1点和圆的位置关系课件(共31张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.2.1点和圆的位置关系课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 757.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-01 00:00:00 | ||
图片预览








文档简介
(共31张PPT)
24.2.1
点和圆的位置关系
1.掌握点与圆的三种位置关系的判定方法.
2.理解不在同一直线上的三个点确定一个圆;理解三角形的外接圆和三角形外心的概念.
3.了解反证法的证明思想.
学习目标(1分钟)
自学指导1(4分钟)
仔细阅读课本92内容,完成练习:
1、点和圆的三种位置关系___________________________.
2、点和圆的位置关系与点到圆心的距离d、圆的半径r之间的关系: 点在圆外 _______;
点在圆上 _______;
点在圆内 _______.
符号“ ”读作_______.它表示_____________________________________________________.
点在圆上,点在圆外,点在圆内
d>r
d=r
d<r
等价于
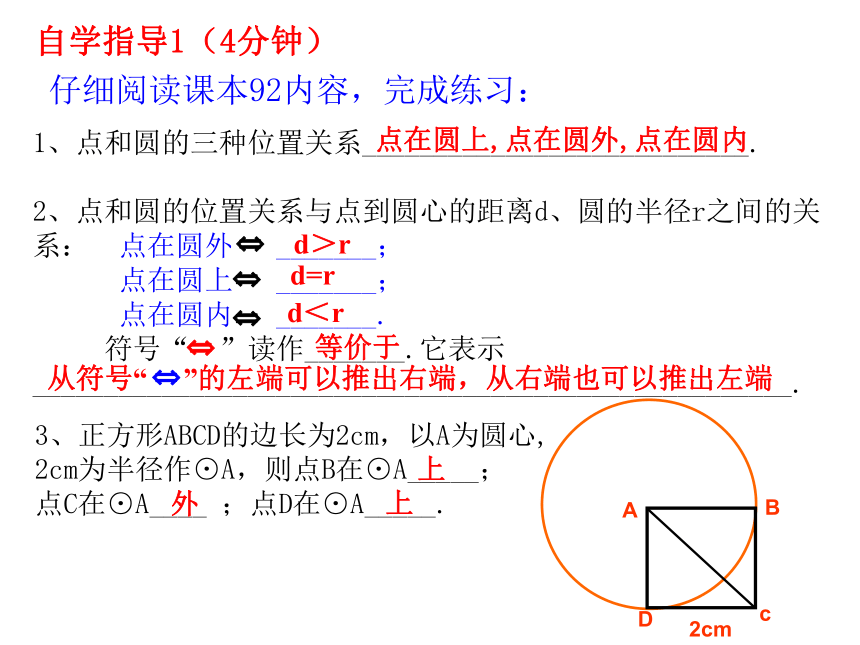
3、正方形ABCD的边长为2cm,以A为圆心,
2cm为半径作⊙A,则点B在⊙A_____;
点C在⊙A____ ;点D在⊙A_____.
上
外
上
如图,设⊙O 的半径为r,A点在圆内,B点在圆上,C点在圆外,那么 OA<r, OB=r, OC>r.
点A在⊙O内
点B在⊙O上
点C在⊙O外
反过来也成立,如果已知点到圆心的距离和圆的半径的关系,就可以判断点和圆的位置关系.
OA<r
OB=r
OC>r
A
B
C
r
点与圆的位置关系
o
设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
P在⊙O上
P在⊙O外
d<r
d=r
d>r
点与圆的位置关系
圆外的点
圆内的点
圆上的点
平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点.
圆的内部可以看成是到圆心的距离小于半径的的点的集合;圆的外部可以看成是到圆心的距离大于半径的点的集合.圆上的点可以看成是到圆心的距离等于半径的点的集合.
【思考】
平面上的一个圆把平面上的点分成哪几部分?
1.⊙O的半径10cm,A、B、C三点到圆心的距离分别为
8cm、10cm、12cm,则点A、B、C与⊙O的位置关系
是:点A在_______;点B在______;点C在_______.
2.⊙O的半径6cm,当OP=6时,点A在________;
当OP___________时,点P在圆内;
当OP___________时,点P不在圆外.
圆内
圆上
圆外
圆上
<6
≤6
自学检测1(4分钟)
3、已知☉O的半径为2015cm,线段OA=2016cm,则点A与☉O的位置关系是( )
A.点A在☉O外 B.点A在☉O上
C.点A在☉O内 D.不能确定
4.点A在以O为圆心,3cm为半径的☉O外,则点A到圆心O的距离d的范围是______.
5.已知矩形ABCD的边长AB=3cm,AD=4cm.
(1)以点A为圆心,4cm为半径作☉A,则点B,C,D与☉A的位置关系如何?
(2)若以A为圆心作☉A,使B,C,D三点中至少有一点在圆内,且至少有一点在圆外,则☉A的半径r的取值范围是什么?
(3)若以A为圆心作☉A,使B,C,D三点中至少有两点在圆内,且至少有一点在圆外,则☉A的半径r的取值范围是什么?
A
d>3cm
解:(1)∵AB=3cm<4cm,∴点B在☉A内;
∵AC= =5cm>4cm,∴点C在☉A外;
∵AD=4cm,∴点D在☉A上.
(2)∵AB若B,C,D三点中至少有一点在圆内,则r>3cm;
若B,C,D三点中至少有一点在圆外,则r<5cm;
∴满足条件的☉A的半径r的取值范围是3cm(3)∵AB若B,C,D三点中至少有两点在圆内,则r>4cm;
若B,C,D三点中至少有一点在圆外,则r<5cm;
∴满足条件的☉A的半径r的取值范围是4cm自学指导2(6分钟)
仔细阅读课本93至94页“思考”之前的内容,完成练习:
1、确定圆的条件
(1)确定一个圆需要确定___________.
(2)过一个点可以画________圆,过两个点可以画________圆.
(3)___________________的三个点确定一个圆.
2、三角形的外接圆和外心
(1)三角形的外接圆:经过三角形的_________可以作一个圆,这个圆叫做三角形的外接圆.
(2)三角形的外心:即三角形_______的圆心,外心是三角形__________________的交点.
锐角三角形的外心在三角形的______;
直角三角形的外心_______________;
钝角三角形的外心________________.
3、三角形三条高线的交点叫三角形的______;三角形三条中线的交点叫三角形的______;三角形三条角平分线的交点叫三角形的______;
三个顶点
外接圆
三条边垂直平分线
圆心和半径
无数个
无数个
不在同一条直线上
内部
是斜边的中点
在三角形的外部
垂心
重心
内心
确定圆的要素
圆心确定其位置,半径确定其大小.只有圆心没有半径,虽圆的位置固定,但大小不定,因而圆不确定;只有半径而没有圆心,虽圆的大小固定,但圆心的位置不定,因而圆也不确定;只有圆心和半径都固定,圆才被唯一确定.
平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
●A
解:无数个,圆心为点A以外任意一点,半径为这点与点A的距离.
平面上有两点A,B,经过已知点A,B的圆有几个?它们的圆心分布有什么特点?
解:无数个.它们的圆心都在线段AB的垂直平分线上,以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
平面上有三点A,B,C,经过A,B,C三点的圆有几个?圆心在哪里?
●
● C
经过B,C两点的圆的圆心在线段
BC的垂直平分线上.
●O
解:经过A,B两点的圆的圆
心在线段AB的垂直平分线上.
●
A
B
●
● C
●O
●
【归纳】
A
B
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
即:不在同一条直线上的三个点确定一个圆.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
注意:不要和到三角形三边距离相等混淆
顶点
三角形的外心就是三角形三条边的垂直平分线的
交点,所以外心到三角形三个顶点的距离相等.
1.一个三角形的外接圆有几个?
2.一个圆的内接三角形有几个?
3.三角形的外心有什么特征?
【想一想】
一个三角形只有一个外接圆.
一个圆的内接三角形有无数个.
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
做一做
作法:1.连结AB,作线段AB的垂直平分线MN;
O
N
M
F
E
A
B
C
已知:不在同一直线上的三点A、B、C
求作:⊙O使它经过点A、B、C
2.连接AC,作线段AC的垂直平分线EF,交MN于点O;
3.以O为圆心,OB为半径作圆。所以⊙O就是所求作的圆。
√
×
√
1.判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆.( ).
(2)任意一个圆有且只有一个内接三角形.( )
(3)三角形的外心到三角形各顶点的距离相等.( )
2.若一个三角形的外心在其中一边上,则此三角形的
形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
3.已知如图,AB为⊙O的直径,P为⊙O 上任意一点P,则点P关于AB的对称点P′与⊙O的位置为( )
A.在⊙O内 B.在⊙O外
C.在⊙O上 D.不能确定
B
C
自学检测2:(6分钟)
4.有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有( )
A.4个 B.3个 C. 2个 D. 1个
5.某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
B
●
●
●
B
A
C
6.三条公路两两相交,交点分别为A、B、C,现计划建一个加油站,要求到三条公路的距离相等,问满足要求的加油站地址有几种情况?
7.如何利用一个直角作圆的直径.
8.如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为
(-2,4),则该圆弧所在圆的圆心坐标是 。
A
C
B
O
P
(-1,1)
解:
1.在圆弧上任取三点A、B、C。
A
B
C
O
2.作线段AB、BC的垂直平分线,其交点O即为圆心。
3.以点O为圆心,OC长为半径作圆。
⊙O即为所求。
9.怎样要将一个如图所示的破损的圆盘复原?
自学指导3(4分钟)
阅读94页“思考”以下的内容,完成练习:
1、求证:过同一条直线上的三个点不可以画圆.
已知:如图,点A、B、C三点在同一条直线l上.
求证:点A、B、C三点不共圆.
证明:假设__________________________________________.
∵ 过点A,B,C三点的圆的圆心即在线段AB的 上,
又在线段BC的 上
如图,作线段AB和线段BC的垂直平分线l1和l2
则,两直线的交点为 .
设这个交点为 ,
∵ ⊥l, ⊥l, 且l1和l2都经过点P
这与“________________________
_________________”矛盾.
∴ 假设“ ”
是错误的.
∴ __________________________不可以画圆.
P
l1
l2
经过同一条直线上的A,B,C三点可以作一个圆
垂直平分线
垂直平分线
圆心
点P
l1
l2
过一点有且只有一条直线
与已知直线垂直
经过同一条直线上的A,B,C三点可以作一个圆
过同一条直线上的三个点
反证法
假设
推理
结论
2.反证法的概念:
对一个命题,先 ,经过推理得出 ,由 ____断定 ,从而得到 .这种方法叫做反证法.
反证法证明问题的三个步骤
(1)_____;(2)_____;(3)_____.
概念中的“矛盾”是指:
_________________________________________________.
假设结论不成立
矛盾
所作假设不正确
原命题成立
矛盾
先作的假设与常与公理、定理、定义或已知条件相矛盾
自学检测3(2分钟)
用反证法证明:两直线平行,同位角相等。
1.点与圆的三种位置关系.
2.不在同一条直线上的三个点确定一个圆.
3.概念:外接圆、外心.
4.反证法.
通过本课时的学习,需要我们掌握:
小结(1分钟)
1.判断对错:
(1)经过两点可以作无数个圆. ( )
(2)三点可以确定一个圆.( )
(3)任何三角形都有外接圆. ( )
(4)任意一个圆有且只有一个内接三角形.( )
2.下列图形一定有外接圆的是( )
A.三角形 B.平行四边形
C.梯形 D.菱形
3.已知a、b、c是△ABC三边长,外接圆的圆心在△ABC一条边上的是( )
A.a=15,b=12,c=1 B.a=5, b=12,c=12
C.a=5, b=12,c=13 D.a=5, b=12,c=14
√
×
√
×
当堂训练(10分钟)
A
C
4.在一个圆中任意引两条直径,顺次连接它们的四个端点组成一个四边形,则这个四边形一定是( )
A.菱形?B.等腰梯形 C.矩形?D.正方形
C
5.已知:Rt△ABC的两直角边为a和b,且a,b是方程
x2-3x+1=0的两根,求:Rt△ABC的外接圆面积.
6.如图,在△ABC中,AB=AC=10,BC=12,求其外接圆的半径.
解:如图,连接AO并延长,交BC于点D.连接OC.
D
又AD过圆心
∴ ∠ADC=900.
在Rt△ADC中,有AD=
设圆O的半径为R,则OD=8-R.
在Rt△ODC中,有OC2=OD2+CD2
即 R2=(8-R)2+62.
24.2.1
点和圆的位置关系
1.掌握点与圆的三种位置关系的判定方法.
2.理解不在同一直线上的三个点确定一个圆;理解三角形的外接圆和三角形外心的概念.
3.了解反证法的证明思想.
学习目标(1分钟)
自学指导1(4分钟)
仔细阅读课本92内容,完成练习:
1、点和圆的三种位置关系___________________________.
2、点和圆的位置关系与点到圆心的距离d、圆的半径r之间的关系: 点在圆外 _______;
点在圆上 _______;
点在圆内 _______.
符号“ ”读作_______.它表示_____________________________________________________.
点在圆上,点在圆外,点在圆内
d>r
d=r
d<r
等价于
3、正方形ABCD的边长为2cm,以A为圆心,
2cm为半径作⊙A,则点B在⊙A_____;
点C在⊙A____ ;点D在⊙A_____.
上
外
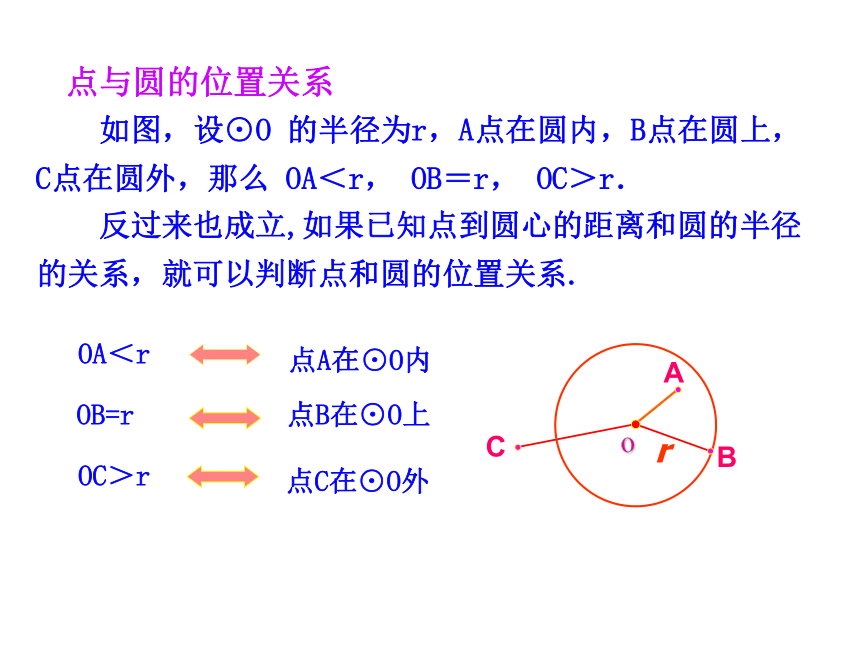
上
如图,设⊙O 的半径为r,A点在圆内,B点在圆上,C点在圆外,那么 OA<r, OB=r, OC>r.
点A在⊙O内
点B在⊙O上
点C在⊙O外
反过来也成立,如果已知点到圆心的距离和圆的半径的关系,就可以判断点和圆的位置关系.
OA<r
OB=r
OC>r
A
B
C
r
点与圆的位置关系
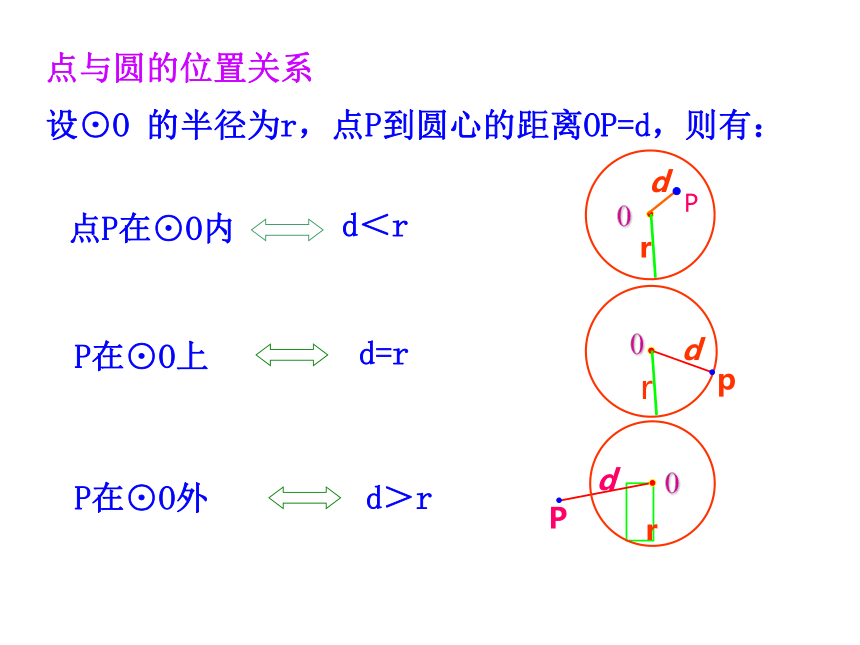
o
设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
P在⊙O上
P在⊙O外
d<r
d=r
d>r
点与圆的位置关系
圆外的点
圆内的点
圆上的点
平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点.
圆的内部可以看成是到圆心的距离小于半径的的点的集合;圆的外部可以看成是到圆心的距离大于半径的点的集合.圆上的点可以看成是到圆心的距离等于半径的点的集合.
【思考】
平面上的一个圆把平面上的点分成哪几部分?
1.⊙O的半径10cm,A、B、C三点到圆心的距离分别为
8cm、10cm、12cm,则点A、B、C与⊙O的位置关系
是:点A在_______;点B在______;点C在_______.
2.⊙O的半径6cm,当OP=6时,点A在________;
当OP___________时,点P在圆内;
当OP___________时,点P不在圆外.
圆内
圆上
圆外
圆上
<6
≤6
自学检测1(4分钟)
3、已知☉O的半径为2015cm,线段OA=2016cm,则点A与☉O的位置关系是( )
A.点A在☉O外 B.点A在☉O上
C.点A在☉O内 D.不能确定
4.点A在以O为圆心,3cm为半径的☉O外,则点A到圆心O的距离d的范围是______.
5.已知矩形ABCD的边长AB=3cm,AD=4cm.
(1)以点A为圆心,4cm为半径作☉A,则点B,C,D与☉A的位置关系如何?
(2)若以A为圆心作☉A,使B,C,D三点中至少有一点在圆内,且至少有一点在圆外,则☉A的半径r的取值范围是什么?
(3)若以A为圆心作☉A,使B,C,D三点中至少有两点在圆内,且至少有一点在圆外,则☉A的半径r的取值范围是什么?
A
d>3cm
解:(1)∵AB=3cm<4cm,∴点B在☉A内;
∵AC= =5cm>4cm,∴点C在☉A外;
∵AD=4cm,∴点D在☉A上.
(2)∵AB
若B,C,D三点中至少有一点在圆外,则r<5cm;
∴满足条件的☉A的半径r的取值范围是3cm
若B,C,D三点中至少有一点在圆外,则r<5cm;
∴满足条件的☉A的半径r的取值范围是4cm
仔细阅读课本93至94页“思考”之前的内容,完成练习:
1、确定圆的条件
(1)确定一个圆需要确定___________.
(2)过一个点可以画________圆,过两个点可以画________圆.
(3)___________________的三个点确定一个圆.
2、三角形的外接圆和外心
(1)三角形的外接圆:经过三角形的_________可以作一个圆,这个圆叫做三角形的外接圆.
(2)三角形的外心:即三角形_______的圆心,外心是三角形__________________的交点.
锐角三角形的外心在三角形的______;
直角三角形的外心_______________;
钝角三角形的外心________________.
3、三角形三条高线的交点叫三角形的______;三角形三条中线的交点叫三角形的______;三角形三条角平分线的交点叫三角形的______;
三个顶点
外接圆
三条边垂直平分线
圆心和半径
无数个
无数个
不在同一条直线上
内部
是斜边的中点
在三角形的外部
垂心
重心
内心
确定圆的要素
圆心确定其位置,半径确定其大小.只有圆心没有半径,虽圆的位置固定,但大小不定,因而圆不确定;只有半径而没有圆心,虽圆的大小固定,但圆心的位置不定,因而圆也不确定;只有圆心和半径都固定,圆才被唯一确定.
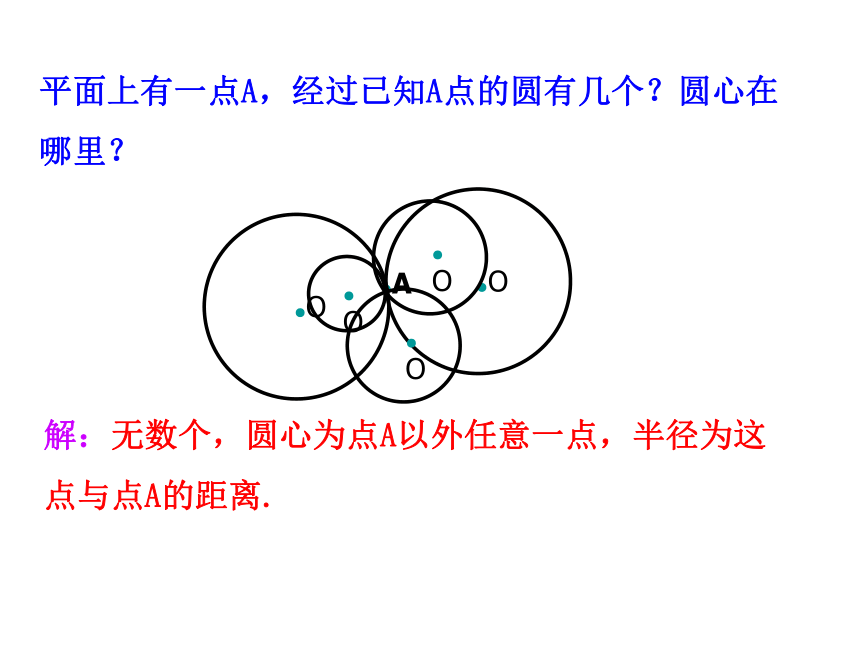
平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
●A
解:无数个,圆心为点A以外任意一点,半径为这点与点A的距离.
平面上有两点A,B,经过已知点A,B的圆有几个?它们的圆心分布有什么特点?
解:无数个.它们的圆心都在线段AB的垂直平分线上,以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
平面上有三点A,B,C,经过A,B,C三点的圆有几个?圆心在哪里?
●
● C
经过B,C两点的圆的圆心在线段
BC的垂直平分线上.
●O
解:经过A,B两点的圆的圆
心在线段AB的垂直平分线上.
●
A
B
●
● C
●O
●
【归纳】
A
B
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
即:不在同一条直线上的三个点确定一个圆.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
注意:不要和到三角形三边距离相等混淆
顶点
三角形的外心就是三角形三条边的垂直平分线的
交点,所以外心到三角形三个顶点的距离相等.
1.一个三角形的外接圆有几个?
2.一个圆的内接三角形有几个?
3.三角形的外心有什么特征?
【想一想】
一个三角形只有一个外接圆.
一个圆的内接三角形有无数个.
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
做一做
作法:1.连结AB,作线段AB的垂直平分线MN;
O
N
M
F
E
A
B
C
已知:不在同一直线上的三点A、B、C
求作:⊙O使它经过点A、B、C
2.连接AC,作线段AC的垂直平分线EF,交MN于点O;
3.以O为圆心,OB为半径作圆。所以⊙O就是所求作的圆。
√
×
√
1.判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆.( ).
(2)任意一个圆有且只有一个内接三角形.( )
(3)三角形的外心到三角形各顶点的距离相等.( )
2.若一个三角形的外心在其中一边上,则此三角形的
形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
3.已知如图,AB为⊙O的直径,P为⊙O 上任意一点P,则点P关于AB的对称点P′与⊙O的位置为( )
A.在⊙O内 B.在⊙O外
C.在⊙O上 D.不能确定
B
C
自学检测2:(6分钟)
4.有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有( )
A.4个 B.3个 C. 2个 D. 1个
5.某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
B
●
●
●
B
A
C
6.三条公路两两相交,交点分别为A、B、C,现计划建一个加油站,要求到三条公路的距离相等,问满足要求的加油站地址有几种情况?
7.如何利用一个直角作圆的直径.
8.如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为
(-2,4),则该圆弧所在圆的圆心坐标是 。
A
C
B
O
P
(-1,1)
解:
1.在圆弧上任取三点A、B、C。
A
B
C
O
2.作线段AB、BC的垂直平分线,其交点O即为圆心。
3.以点O为圆心,OC长为半径作圆。
⊙O即为所求。
9.怎样要将一个如图所示的破损的圆盘复原?
自学指导3(4分钟)
阅读94页“思考”以下的内容,完成练习:
1、求证:过同一条直线上的三个点不可以画圆.
已知:如图,点A、B、C三点在同一条直线l上.
求证:点A、B、C三点不共圆.
证明:假设__________________________________________.
∵ 过点A,B,C三点的圆的圆心即在线段AB的 上,
又在线段BC的 上
如图,作线段AB和线段BC的垂直平分线l1和l2
则,两直线的交点为 .
设这个交点为 ,
∵ ⊥l, ⊥l, 且l1和l2都经过点P
这与“________________________
_________________”矛盾.
∴ 假设“ ”
是错误的.
∴ __________________________不可以画圆.
P
l1
l2
经过同一条直线上的A,B,C三点可以作一个圆
垂直平分线
垂直平分线
圆心
点P
l1
l2
过一点有且只有一条直线
与已知直线垂直
经过同一条直线上的A,B,C三点可以作一个圆
过同一条直线上的三个点
反证法
假设
推理
结论
2.反证法的概念:
对一个命题,先 ,经过推理得出 ,由 ____断定 ,从而得到 .这种方法叫做反证法.
反证法证明问题的三个步骤
(1)_____;(2)_____;(3)_____.
概念中的“矛盾”是指:
_________________________________________________.
假设结论不成立
矛盾
所作假设不正确
原命题成立
矛盾
先作的假设与常与公理、定理、定义或已知条件相矛盾
自学检测3(2分钟)
用反证法证明:两直线平行,同位角相等。
1.点与圆的三种位置关系.
2.不在同一条直线上的三个点确定一个圆.
3.概念:外接圆、外心.
4.反证法.
通过本课时的学习,需要我们掌握:
小结(1分钟)
1.判断对错:
(1)经过两点可以作无数个圆. ( )
(2)三点可以确定一个圆.( )
(3)任何三角形都有外接圆. ( )
(4)任意一个圆有且只有一个内接三角形.( )
2.下列图形一定有外接圆的是( )
A.三角形 B.平行四边形
C.梯形 D.菱形
3.已知a、b、c是△ABC三边长,外接圆的圆心在△ABC一条边上的是( )
A.a=15,b=12,c=1 B.a=5, b=12,c=12
C.a=5, b=12,c=13 D.a=5, b=12,c=14
√
×
√
×
当堂训练(10分钟)
A
C
4.在一个圆中任意引两条直径,顺次连接它们的四个端点组成一个四边形,则这个四边形一定是( )
A.菱形?B.等腰梯形 C.矩形?D.正方形
C
5.已知:Rt△ABC的两直角边为a和b,且a,b是方程
x2-3x+1=0的两根,求:Rt△ABC的外接圆面积.
6.如图,在△ABC中,AB=AC=10,BC=12,求其外接圆的半径.
解:如图,连接AO并延长,交BC于点D.连接OC.
D
又AD过圆心
∴ ∠ADC=900.
在Rt△ADC中,有AD=
设圆O的半径为R,则OD=8-R.
在Rt△ODC中,有OC2=OD2+CD2
即 R2=(8-R)2+62.
同课章节目录
