高中数学人教A版必修5第二章2.1数列的概念与简单表示(二)课件(共19张PPT)
文档属性
| 名称 | 高中数学人教A版必修5第二章2.1数列的概念与简单表示(二)课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-02 15:21:44 | ||
图片预览


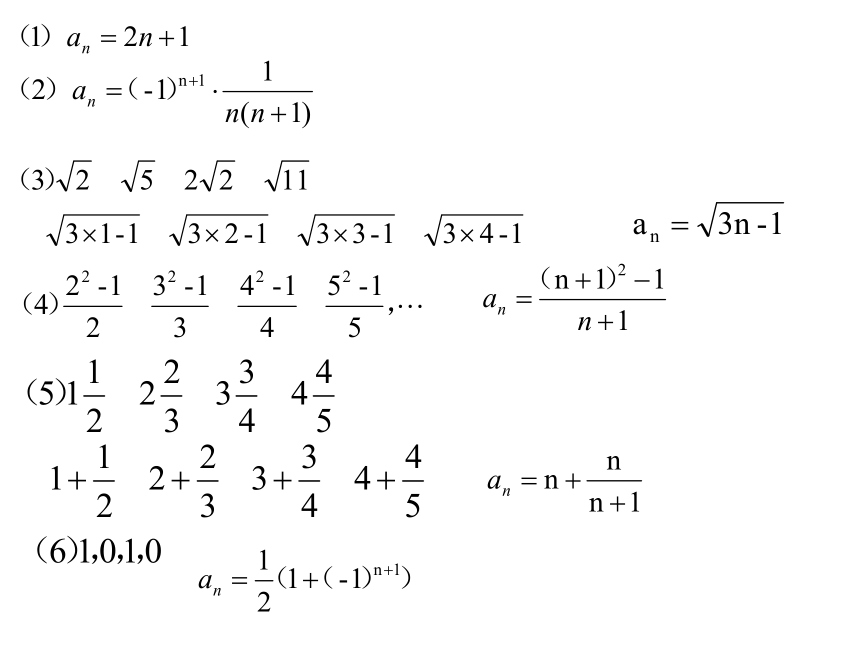
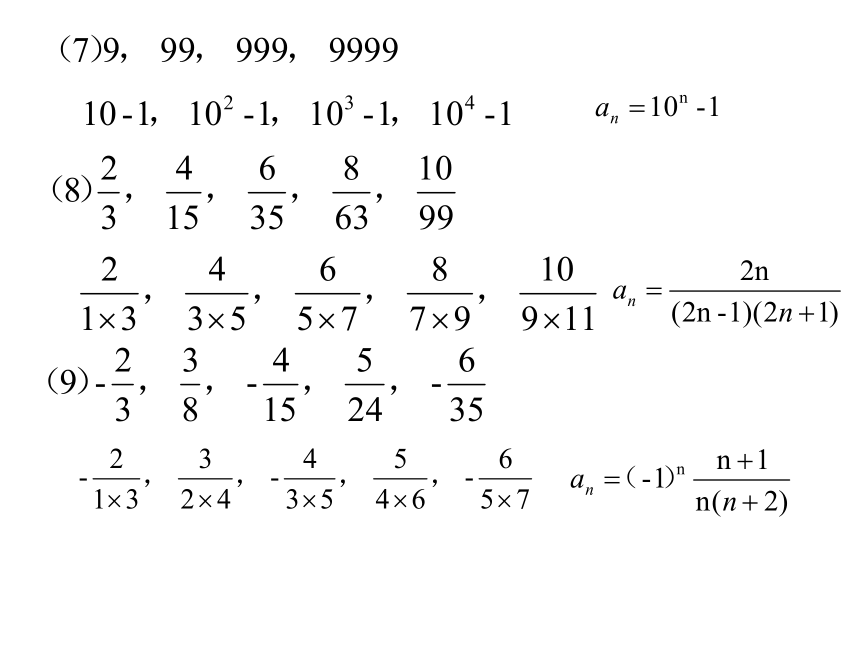



文档简介
(共19张PPT)
2.1数列的概念与简单表示(二)
练习:根据下面数列的前n项的值,写出数列的一个通项公式:
1 2 3 4 5 …n
序号n
递推公式也是数列的一种表示方法。
已知数列{an}的首项(或前几项),且任一项an与它的前一项an-1(或前几项)间的关系可用一个式子来表示,那么这个式子就叫做这个数列的递推公式。
数列的递推公式
如数列1,3,6,10的递推公式可表示为
a1=1,an=an-1+n(n>1)
解:由题意可知
练习1、P31 练习第2题 各班学号 号学生回答。
练习2、
已知数列 满足
(1)求
(2)试写出 的一个通项公式。
直接观察猜想,即不完全归纳法;
利用递推公式求通项公式,常用累加、累乘、周期性等知识。
例3 、已知数列 的通项为 求
(1)该数列中有多少项为负数;
(2) 为何值时, 有最小值,并求此最小值.
小结: 本节课学习的主要内容有:
1、直接观察猜想法求通项公式
2、用累加、累乘、周期性等知识求通项公式
3、求数列的最大、最小项,最值
补充1:求以下各数列的通项公式
补充2(1)已知数列 满足 求 ;
(2)已知数列 满足 求 ;
(3)已知数列 满足 求 ;
(4)设 是首项为1的正项数列,且
2.1数列的概念与简单表示(二)
练习:根据下面数列的前n项的值,写出数列的一个通项公式:
1 2 3 4 5 …n
序号n
递推公式也是数列的一种表示方法。
已知数列{an}的首项(或前几项),且任一项an与它的前一项an-1(或前几项)间的关系可用一个式子来表示,那么这个式子就叫做这个数列的递推公式。
数列的递推公式
如数列1,3,6,10的递推公式可表示为
a1=1,an=an-1+n(n>1)
解:由题意可知
练习1、P31 练习第2题 各班学号 号学生回答。
练习2、
已知数列 满足
(1)求
(2)试写出 的一个通项公式。
直接观察猜想,即不完全归纳法;
利用递推公式求通项公式,常用累加、累乘、周期性等知识。
例3 、已知数列 的通项为 求
(1)该数列中有多少项为负数;
(2) 为何值时, 有最小值,并求此最小值.
小结: 本节课学习的主要内容有:
1、直接观察猜想法求通项公式
2、用累加、累乘、周期性等知识求通项公式
3、求数列的最大、最小项,最值
补充1:求以下各数列的通项公式
补充2(1)已知数列 满足 求 ;
(2)已知数列 满足 求 ;
(3)已知数列 满足 求 ;
(4)设 是首项为1的正项数列,且
