人教版高中物理必修二第六章6.5.2补充双星与多星问题课件 (共18张PPT)
文档属性
| 名称 | 人教版高中物理必修二第六章6.5.2补充双星与多星问题课件 (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 463.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-01 14:05:41 | ||
图片预览






文档简介
(共18张PPT)
6.7 双星与多星问题
高中阶段对天体的运动研究有三大类:
一、环绕与被环绕问题(又叫中心环绕问题)
特点:
⑴环绕天体的质量远小于被环绕天体的质量(又叫中心天体)
⑵认为中心天体静止不动,环绕天体绕中心天体的中心做圆周运动。
⑶中心天体的对环绕天体的引力提供向心力,忽略周围其他天体的引力。
⑷主要问题有:行星绕恒星、卫星绕行星的运动
二、双星问题
1、定义:两个质量相当、相对孤立的天体在相互引力的作用下绕两天体连线上的某点做圆周运动。
2、特点:如图所示
设两天体的质量分别为M1、M2;两天体中心间的距离为L。试分析两天体做圆周运动的角速度的关系,并求两天体做圆周运动的周期和半径。
⑴绕两天体的质心运动,两天体的角速度、周期相同;
⑵半径与质量成反比;
⑶
周期只决定两天体之间的距离和总质量。
例题1:质量为M的恒星A和质量为m的恒星B(M>m),在它们之间的万有引力作用下有规则地运动着.如图所示,已知恒星B以某一定点C为中心、半径为a的圆周上做匀速圆周运动(图中没有表示出恒星A)。设万有引力常量为G,恒星的大小可忽略不计。
⑴恒星A与点C间的距离是多少?
⑵在图中画出恒星A运动的轨道和位置;
⑶计算恒星A的运行速率v.
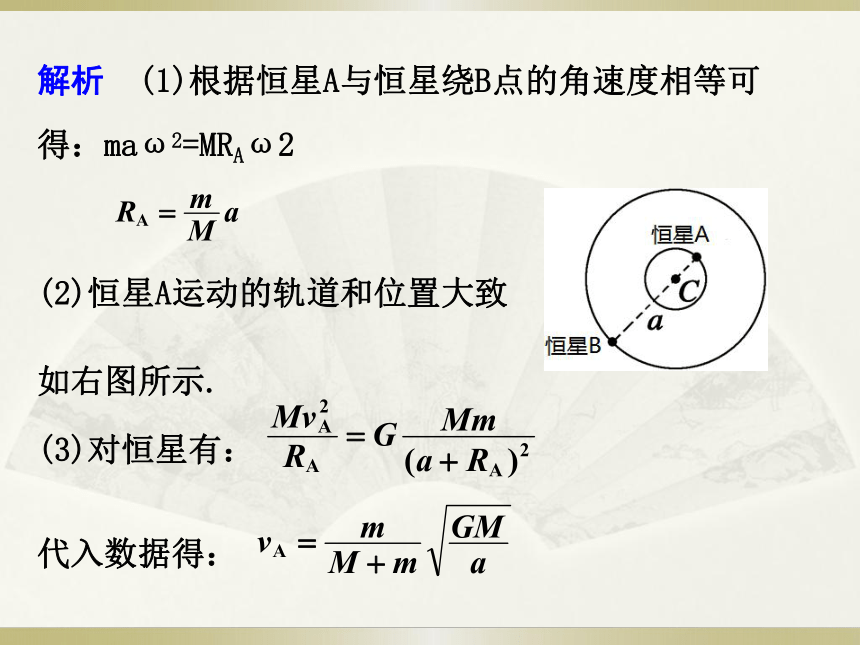
解析 (1)根据恒星A与恒星绕B点的角速度相等可
得:maω2=MRAω2
(2)恒星A运动的轨道和位置大致
如右图所示.
(3)对恒星有:
代入数据得:
例题2:在地月系统中,若忽略其它星球的影响,可以将月球和地球看成双星问题,月球绕其轨道中心运行为的周期记为T1。但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期T2。已知地球和月球的质量分别为5.98×1024kg 和 7.35 ×1022kg 。求T2与T1两者平方之比。(结果保留3数)
例题3:天文学家观测河外星系麦哲伦云时,发现了LMCX?3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响。A、B围绕两者的连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示。引力常量为G,观测测得到可见星A的速率v和运行周期T.
⑴可见星A所受暗星B的引力FA可等效为位于O点处质量为m′的星体(视为质点)对它的引力,设A和B的质量分别为m1、m2,试求m′(用m1、m2表示);
⑵求暗星B的质量m2与可见星A的速率v、运行周期T和质量m1之间的关系式.
解析:(1)由
得:
又由: 得:
(2)由 得:
由 得:
再由: 可得:
三、多星问题
1、多星系统:几个质量相当的天体,在相互的万有引力的作用下,绕某点长期稳定地做匀速圆周运动。
2、特点:
⑴各天体做圆周运动有一个共同的圆心,且圆心为几个天体的质心。
⑵所有天体做圆周运动的角速度、周期都相同。
⑶每个天体受到其它天体引力的矢量和为该天体做圆周运动的向心力。
3、三星模型
⑴构成一条直线
①三个天体质量都相同,一定构成图甲的图形。
②两个天体的质量相同,一个不同,一定构成图乙的图形。
请大家进行受力分析,列出圆周运动的基本方程。
⑵构成三角形
①三个天体质量都相同,一定构成一个等边三角形,图丙所示。
②两个天体质量相同,一个不同,也构成一个等腰三角形,图丁所示。
丙
丁
请大家进行受力分析,列出圆周运动的基本方程。
4、四星模型
⑴四个质量相等的天体构成一个等边三角形图⑴或正方形图⑵
⑵三个质量相等,构成一个等边三角形图⑶ 。
请大家进行受力分析,列出圆周运动的基本方程。
图(1)
图(2)
图(3)
例题4: 如图所示,设三颗恒星质量相同,均为m,间距也相同,它们仅在彼此的引力作用下绕着三星系统的中心点O做匀速圆周运动。它们自身的大小与它们之间的距离相比可以忽略。请你通过计算定量说明:三星系统的运转半径的三次方及运转周期的二次方的比值应为多少。(引力常量为G)
例题5:设三个质量均为m的天体,组成稳定的直线模型的三星系统,相邻两天体之间的距离为R,边缘两天体绕中央天体做匀速圆周运动。
⑴求边缘两天体做圆周运动的周期。
⑵假设这三个天体组成一个等边三角形,绕三角形的中心做匀速圆周运动。若运动的周期等于此前直线形模型的周期。求三角模型下两天体间的距离。
例题6:由三颗星体构成的系统,忽略其他星体对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动(图示为A、B、C三颗星体质量不相同时的一般情况).若A星体质量为2m,B、C两星体的质量均为m,三角形的边长为a,求:
(1)A星体所受合力大小FA;
(2)B星体所受合力大小FB;
(3)C星体的轨道半径RC;
(4)三星体做圆周运动的周期T.
特别强调:
⑴环绕和被环绕与双星问题之间相同处是:两天体之间的引力提供向心力。不同之处是:环绕和被环绕问题中,两天体之间的距离与轨道半径相等;而双星问题中,两天体之间的距离不同于轨道半径。
⑵多星问题则是每各天体受多个引力作用,引力的为合力每个天体提供向心力。且轨道半径半径与天体之间的距离也不同。对多星问题要进行受力分析求引力的合成,同时根据天体之间的距离、排列情况确定各天体运动的半径。
⑶引力公式中的r与向心加速度公式中r的区别:
前者:两天体中心间的距离,
后者:圆周运动的半径。只有环绕与被环绕问题中两者才相等。
6.7 双星与多星问题
高中阶段对天体的运动研究有三大类:
一、环绕与被环绕问题(又叫中心环绕问题)
特点:
⑴环绕天体的质量远小于被环绕天体的质量(又叫中心天体)
⑵认为中心天体静止不动,环绕天体绕中心天体的中心做圆周运动。
⑶中心天体的对环绕天体的引力提供向心力,忽略周围其他天体的引力。
⑷主要问题有:行星绕恒星、卫星绕行星的运动
二、双星问题
1、定义:两个质量相当、相对孤立的天体在相互引力的作用下绕两天体连线上的某点做圆周运动。
2、特点:如图所示
设两天体的质量分别为M1、M2;两天体中心间的距离为L。试分析两天体做圆周运动的角速度的关系,并求两天体做圆周运动的周期和半径。
⑴绕两天体的质心运动,两天体的角速度、周期相同;
⑵半径与质量成反比;
⑶
周期只决定两天体之间的距离和总质量。
例题1:质量为M的恒星A和质量为m的恒星B(M>m),在它们之间的万有引力作用下有规则地运动着.如图所示,已知恒星B以某一定点C为中心、半径为a的圆周上做匀速圆周运动(图中没有表示出恒星A)。设万有引力常量为G,恒星的大小可忽略不计。
⑴恒星A与点C间的距离是多少?
⑵在图中画出恒星A运动的轨道和位置;
⑶计算恒星A的运行速率v.
解析 (1)根据恒星A与恒星绕B点的角速度相等可
得:maω2=MRAω2
(2)恒星A运动的轨道和位置大致
如右图所示.
(3)对恒星有:
代入数据得:
例题2:在地月系统中,若忽略其它星球的影响,可以将月球和地球看成双星问题,月球绕其轨道中心运行为的周期记为T1。但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期T2。已知地球和月球的质量分别为5.98×1024kg 和 7.35 ×1022kg 。求T2与T1两者平方之比。(结果保留3数)
例题3:天文学家观测河外星系麦哲伦云时,发现了LMCX?3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响。A、B围绕两者的连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示。引力常量为G,观测测得到可见星A的速率v和运行周期T.
⑴可见星A所受暗星B的引力FA可等效为位于O点处质量为m′的星体(视为质点)对它的引力,设A和B的质量分别为m1、m2,试求m′(用m1、m2表示);
⑵求暗星B的质量m2与可见星A的速率v、运行周期T和质量m1之间的关系式.
解析:(1)由
得:
又由: 得:
(2)由 得:
由 得:
再由: 可得:
三、多星问题
1、多星系统:几个质量相当的天体,在相互的万有引力的作用下,绕某点长期稳定地做匀速圆周运动。
2、特点:
⑴各天体做圆周运动有一个共同的圆心,且圆心为几个天体的质心。
⑵所有天体做圆周运动的角速度、周期都相同。
⑶每个天体受到其它天体引力的矢量和为该天体做圆周运动的向心力。
3、三星模型
⑴构成一条直线
①三个天体质量都相同,一定构成图甲的图形。
②两个天体的质量相同,一个不同,一定构成图乙的图形。
请大家进行受力分析,列出圆周运动的基本方程。
⑵构成三角形
①三个天体质量都相同,一定构成一个等边三角形,图丙所示。
②两个天体质量相同,一个不同,也构成一个等腰三角形,图丁所示。
丙
丁
请大家进行受力分析,列出圆周运动的基本方程。
4、四星模型
⑴四个质量相等的天体构成一个等边三角形图⑴或正方形图⑵
⑵三个质量相等,构成一个等边三角形图⑶ 。
请大家进行受力分析,列出圆周运动的基本方程。
图(1)
图(2)
图(3)
例题4: 如图所示,设三颗恒星质量相同,均为m,间距也相同,它们仅在彼此的引力作用下绕着三星系统的中心点O做匀速圆周运动。它们自身的大小与它们之间的距离相比可以忽略。请你通过计算定量说明:三星系统的运转半径的三次方及运转周期的二次方的比值应为多少。(引力常量为G)
例题5:设三个质量均为m的天体,组成稳定的直线模型的三星系统,相邻两天体之间的距离为R,边缘两天体绕中央天体做匀速圆周运动。
⑴求边缘两天体做圆周运动的周期。
⑵假设这三个天体组成一个等边三角形,绕三角形的中心做匀速圆周运动。若运动的周期等于此前直线形模型的周期。求三角模型下两天体间的距离。
例题6:由三颗星体构成的系统,忽略其他星体对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动(图示为A、B、C三颗星体质量不相同时的一般情况).若A星体质量为2m,B、C两星体的质量均为m,三角形的边长为a,求:
(1)A星体所受合力大小FA;
(2)B星体所受合力大小FB;
(3)C星体的轨道半径RC;
(4)三星体做圆周运动的周期T.
特别强调:
⑴环绕和被环绕与双星问题之间相同处是:两天体之间的引力提供向心力。不同之处是:环绕和被环绕问题中,两天体之间的距离与轨道半径相等;而双星问题中,两天体之间的距离不同于轨道半径。
⑵多星问题则是每各天体受多个引力作用,引力的为合力每个天体提供向心力。且轨道半径半径与天体之间的距离也不同。对多星问题要进行受力分析求引力的合成,同时根据天体之间的距离、排列情况确定各天体运动的半径。
⑶引力公式中的r与向心加速度公式中r的区别:
前者:两天体中心间的距离,
后者:圆周运动的半径。只有环绕与被环绕问题中两者才相等。
