19.2.2 一次函数 同步练习(含解析)
文档属性
| 名称 | 19.2.2 一次函数 同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-01 00:00:00 | ||
图片预览


文档简介
初中数学人教版八年级下学期 第十九章 19.2.2 一次函数
一、单选题
1.下列函数中y是x的一次函数的是(? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
2.一次函数y=kx﹣1的图像经过点P,且y的值随x值的增大而增大,则点P的坐标可以为(?? )
A.?(﹣5,3)???????????????????????B.?(1,﹣3)???????????????????????C.?(2,2)???????????????????????D.?(5,﹣1)
3.直线 不经过的象限是 (??? )
A.?第四象限???????????????????????????B.?第三象限???????????????????????????C.?第二象限???????????????????????????D.?第一象限
4.一根蜡烛长30cm,点燃后每小时燃烧5cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(小时)之间的函数关系用图象可以表示为图中的( ???) 21cnjy.com
A.???????????B.???????????C.???????????D.?
5.对于函数y=-3x+1,下列说法不正确的是( ???)
A.?它的图象必经过点(1,-2) B.?它的图象经过第一、二、四象限 C.?C当x> 时,y>0 D.?它的图象与直线y=-3x平行21·世纪*教育网
6.将直线y=﹣2x+1向上平移2个单位长度,所得到的直线解析式为(?? )
A.?y=2x+1?????????????????????????B.?y=﹣2x﹣1?????????????????????????C.?y=2x+3?????????????????????????D.?y=﹣2x+3
7.下列函数:(1) y=x ;(2) ;(3) ;(4) ;(5)s=12t;(6)y=30-4x中,是一次函数的有?? ( ???) www-2-1-cnjy-com
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
二、填空题
8.若点A(2,y1),B(﹣1,y2)都在直线y=﹣2x+1上,则y1与y2的大小关系是________.
9.已知一辆出租车油箱内剩余油48L,一般行驶一小时耗油8L,则该车油箱内剩余流量
y(L)和行驶时间x(时)之间的函数关系式是________(不写自变量取值范围)
10.若点A(3,2)、B(-1,-6)、C(a,-2)在同一条直线上,则a=________. 2-1-c-n-j-y
三、解答题
11.一次函数y=kx+b中(k、b为常数,k≠0),若-3≤x≤2,则-1≤y≤9,求一次函数的解析式.
四、作图题
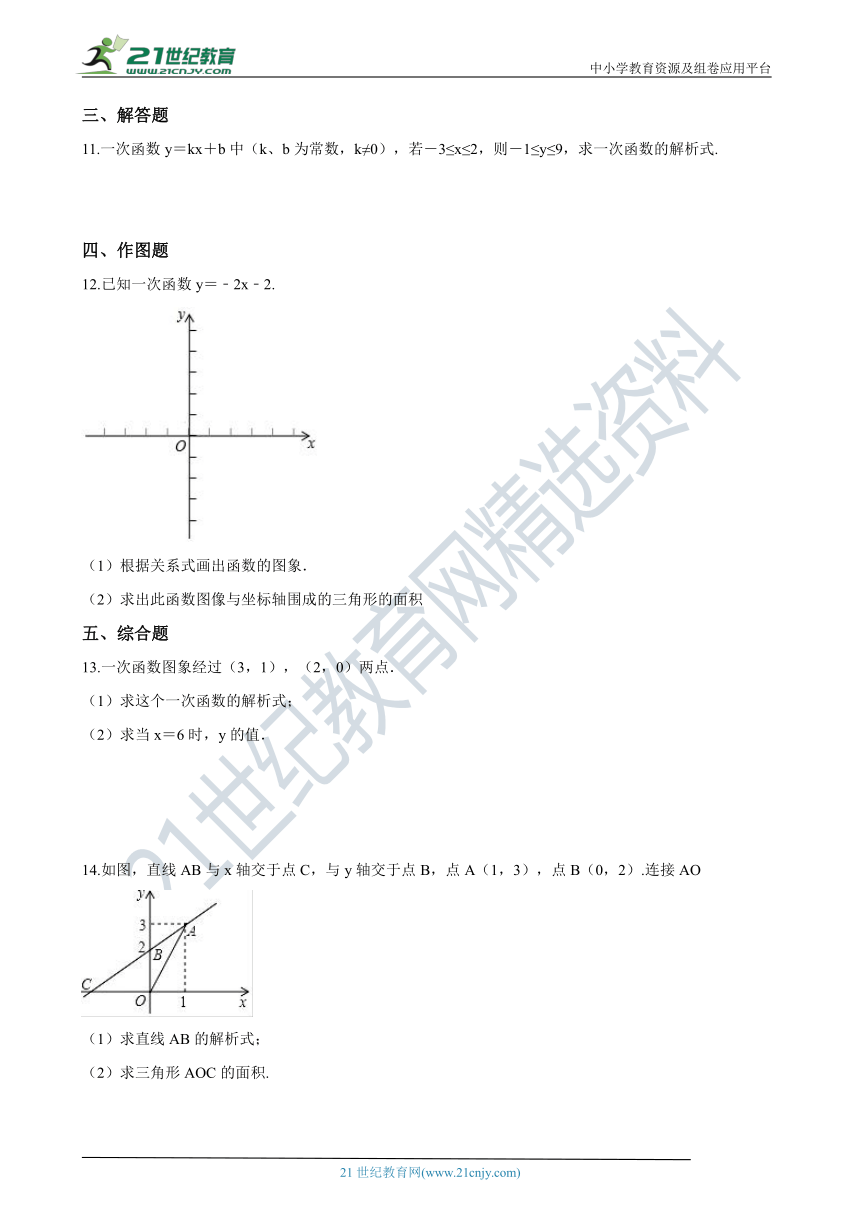
12.已知一次函数y=﹣2x﹣2.
(1)根据关系式画出函数的图象.
(2)求出此函数图像与坐标轴围成的三角形的面积
五、综合题
13.一次函数图象经过(3,1),(2,0)两点.
(1)求这个一次函数的解析式;
(2)求当x=6时,y的值.
14.如图,直线AB与x轴交于点C,与y轴交于点B,点A(1,3),点B(0,2).连接AO
(1)求直线AB的解析式;
(2)求三角形AOC的面积.
答案解析部分
一、单选题
1. B
A.含有分式,A不符合题意;
B.满足一次函数的概念,B符合题意.
C.含有分式,C不符合题意.
D.含有二次项,D不符合题意.
故答案为:B.
分析:利用一次函数的定义即能找到答案.
2. C
解:∵一次函数y随x的增大而增大 ∴k>0 A.将坐标代入一次函数,-5k-1=3,解得k=<0,错误; B.将坐标代入一次函数,k-1=-3,解得k=-2<0,错误; C.将坐标代入一次函数,2k-1=2,解得k=>0,正确; D.将坐标代入一次函数,5k-1=-1,解得k=0,错误。 21·cn·jy·com
故答案为:C.
分析:根据题意,可知k>0,根据每个选项的坐标进行判断即可得到答案。
3. B
解:∵ 中,k=-2<0,b=3>0,
∴一次函数过第一、二、四象限,不经过第三象限,
故答案为:B.
分析:根据一次函数的性质进行选择即可.
4. B
解:根据题意可知,燃烧时间为t,长度为h ∴h=30-5t(0≤t≤6)
故答案为:B.
分析:根据题意,即可得到蜡烛长度变化的函数解析式,求出t的范围即可进行判断。
5. C
解:A.当x=1时,y=-2,正确; B.函数经过一、二、四象限,正确; C.令y>0,即-3x+1>0,解得x<, 错误; D.∵两个直线的斜率相等,∴图象与直线平行,正确。 21*cnjy*com
故答案为:C.
分析:根据一次函数的性质进行判断即可得到答案。
6. D
解:由“上加下减”的原则可知,把直线y=﹣2x+1上平移2个单位长度后所得直线的解析式为:y=﹣2x+12,即y=﹣2x+3 www.21-cn-jy.com
故答案为:D.
分析:直接根据“上加下减”的原则进行解答即可.
7. D
解:(1) y=x,是一次函数 ;(2) ,是一次函数;(3) ,不是一次函数;(4) ,是一次函数;(5)s=12t,是一次函数;(6)y=30-4x,是一次函数,共5个. 【来源:21cnj*y.co*m】
故答案为:D.
分析:直接利用一次函数的一般形式y=kx+b(k≠0)分析得出答案.
二、填空题
8. y1<y2
∵直线y=?2x+1的比例系数为?2,
∴y随x的增大而减小,
∵2>?1,
∴ ,
故答案为 .
分析:由所给直线解析式的比例系数为负数可得y将随x的增大而减小.
9. y=48-8x
依题意有:y=48-8x.
分析:根据余油量=原有油量-用油量得出.
10. 1
解:将点A(3,2)、B(-1,-6)代入y=kx+b( ),得到 ,从而求得 ,即一次函数解析式为 ,此时代入C(a,-2),得到 ,求出 .
分析:根据已知条件点A(3,2)、B(-1,-6) 在同一条直线上,利用待定系数法求得一次函数解析式,代入C点坐标即可求得a值.21世纪教育网版权所有
三、解答题
11. 解:当k>0时,将(-3,-1),(2,9)代入y=kx+b,
得:
解得:
∴一次函数的解析式为y=2x+5;
当k<0时,将(-3,9),(2,-1)代入y=kx+b,
得:
解得:
∴一次函数的解析式为y=-2x+3.
综上所述:一次函数解析式为y=2x+5或y=-2x+3.
分析:分k>0及k<0两种情况,利用待定系数法可求出一次函数的解析式,此题得解.
四、作图题
12. (1)解:当x=0时,y=-2,即函数图象与y轴交点坐标为(0,-2),
当y=0时,x=-1,即函数图象与x轴交点坐标为(-1,0),
函数图象如图所示:
(2)解:由图可得:OA=1,OB=2,S△OAB= .
分析:(1)先求出函数与x、y轴的交点坐标,再过这两点画直线即可;(2)如图所示,先求得OA与OB的长度,再根据三角形面积公式进行计算即可.2·1·c·n·j·y
五、综合题
13. (1)解:设一次函数解析式为y=kx+b,
把(3,1),(2,0)代入得 ,解得 ,
所以一次函数解析式为y=x﹣2
(2)解:当x=6时,y=x﹣2=6﹣2=4.
分析:(1)利用待定系数法求一次函数解析式;(2)利用(1)中解析式计算自变量为6所对应的函数值即可.【来源:21·世纪·教育·网】
14. (1)解:设直线AB的解析式,
把点A(1,3),B(0,2)代入解析式得: ,
解得:k=1,b=2,
把k=1,b=2代入
得:y=x+2,
直线AB的解析式:y=x+2
(2)解:把y=0代入y=x+2得:x+2=0,
解得:x=﹣2,
∴点C的坐标为(﹣2,0),
∴OC=2,
∵△AOC的底为2,△AOC的高为点A的纵坐标3,
∴S△ABC=2×3× =3,
故三角形AOC的面积为3.
分析:(1)设直线AB的解析式为y=kx+b,把A、B的坐标代入求出k、b的值即可,(2)把y=0代入(1)所求出的解析式,便能求出C点坐标,从而利用三角形的面积公式求出三角形AOC的面积即可.21教育网
一、单选题
1.下列函数中y是x的一次函数的是(? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
2.一次函数y=kx﹣1的图像经过点P,且y的值随x值的增大而增大,则点P的坐标可以为(?? )
A.?(﹣5,3)???????????????????????B.?(1,﹣3)???????????????????????C.?(2,2)???????????????????????D.?(5,﹣1)
3.直线 不经过的象限是 (??? )
A.?第四象限???????????????????????????B.?第三象限???????????????????????????C.?第二象限???????????????????????????D.?第一象限
4.一根蜡烛长30cm,点燃后每小时燃烧5cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(小时)之间的函数关系用图象可以表示为图中的( ???) 21cnjy.com
A.???????????B.???????????C.???????????D.?
5.对于函数y=-3x+1,下列说法不正确的是( ???)
A.?它的图象必经过点(1,-2) B.?它的图象经过第一、二、四象限 C.?C当x> 时,y>0 D.?它的图象与直线y=-3x平行21·世纪*教育网
6.将直线y=﹣2x+1向上平移2个单位长度,所得到的直线解析式为(?? )
A.?y=2x+1?????????????????????????B.?y=﹣2x﹣1?????????????????????????C.?y=2x+3?????????????????????????D.?y=﹣2x+3
7.下列函数:(1) y=x ;(2) ;(3) ;(4) ;(5)s=12t;(6)y=30-4x中,是一次函数的有?? ( ???) www-2-1-cnjy-com
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
二、填空题
8.若点A(2,y1),B(﹣1,y2)都在直线y=﹣2x+1上,则y1与y2的大小关系是________.
9.已知一辆出租车油箱内剩余油48L,一般行驶一小时耗油8L,则该车油箱内剩余流量
y(L)和行驶时间x(时)之间的函数关系式是________(不写自变量取值范围)
10.若点A(3,2)、B(-1,-6)、C(a,-2)在同一条直线上,则a=________. 2-1-c-n-j-y
三、解答题
11.一次函数y=kx+b中(k、b为常数,k≠0),若-3≤x≤2,则-1≤y≤9,求一次函数的解析式.
四、作图题
12.已知一次函数y=﹣2x﹣2.
(1)根据关系式画出函数的图象.
(2)求出此函数图像与坐标轴围成的三角形的面积
五、综合题
13.一次函数图象经过(3,1),(2,0)两点.
(1)求这个一次函数的解析式;
(2)求当x=6时,y的值.
14.如图,直线AB与x轴交于点C,与y轴交于点B,点A(1,3),点B(0,2).连接AO
(1)求直线AB的解析式;
(2)求三角形AOC的面积.
答案解析部分
一、单选题
1. B
A.含有分式,A不符合题意;
B.满足一次函数的概念,B符合题意.
C.含有分式,C不符合题意.
D.含有二次项,D不符合题意.
故答案为:B.
分析:利用一次函数的定义即能找到答案.
2. C
解:∵一次函数y随x的增大而增大 ∴k>0 A.将坐标代入一次函数,-5k-1=3,解得k=<0,错误; B.将坐标代入一次函数,k-1=-3,解得k=-2<0,错误; C.将坐标代入一次函数,2k-1=2,解得k=>0,正确; D.将坐标代入一次函数,5k-1=-1,解得k=0,错误。 21·cn·jy·com
故答案为:C.
分析:根据题意,可知k>0,根据每个选项的坐标进行判断即可得到答案。
3. B
解:∵ 中,k=-2<0,b=3>0,
∴一次函数过第一、二、四象限,不经过第三象限,
故答案为:B.
分析:根据一次函数的性质进行选择即可.
4. B
解:根据题意可知,燃烧时间为t,长度为h ∴h=30-5t(0≤t≤6)
故答案为:B.
分析:根据题意,即可得到蜡烛长度变化的函数解析式,求出t的范围即可进行判断。
5. C
解:A.当x=1时,y=-2,正确; B.函数经过一、二、四象限,正确; C.令y>0,即-3x+1>0,解得x<, 错误; D.∵两个直线的斜率相等,∴图象与直线平行,正确。 21*cnjy*com
故答案为:C.
分析:根据一次函数的性质进行判断即可得到答案。
6. D
解:由“上加下减”的原则可知,把直线y=﹣2x+1上平移2个单位长度后所得直线的解析式为:y=﹣2x+12,即y=﹣2x+3 www.21-cn-jy.com
故答案为:D.
分析:直接根据“上加下减”的原则进行解答即可.
7. D
解:(1) y=x,是一次函数 ;(2) ,是一次函数;(3) ,不是一次函数;(4) ,是一次函数;(5)s=12t,是一次函数;(6)y=30-4x,是一次函数,共5个. 【来源:21cnj*y.co*m】
故答案为:D.
分析:直接利用一次函数的一般形式y=kx+b(k≠0)分析得出答案.
二、填空题
8. y1<y2
∵直线y=?2x+1的比例系数为?2,
∴y随x的增大而减小,
∵2>?1,
∴ ,
故答案为 .
分析:由所给直线解析式的比例系数为负数可得y将随x的增大而减小.
9. y=48-8x
依题意有:y=48-8x.
分析:根据余油量=原有油量-用油量得出.
10. 1
解:将点A(3,2)、B(-1,-6)代入y=kx+b( ),得到 ,从而求得 ,即一次函数解析式为 ,此时代入C(a,-2),得到 ,求出 .
分析:根据已知条件点A(3,2)、B(-1,-6) 在同一条直线上,利用待定系数法求得一次函数解析式,代入C点坐标即可求得a值.21世纪教育网版权所有
三、解答题
11. 解:当k>0时,将(-3,-1),(2,9)代入y=kx+b,
得:
解得:
∴一次函数的解析式为y=2x+5;
当k<0时,将(-3,9),(2,-1)代入y=kx+b,
得:
解得:
∴一次函数的解析式为y=-2x+3.
综上所述:一次函数解析式为y=2x+5或y=-2x+3.
分析:分k>0及k<0两种情况,利用待定系数法可求出一次函数的解析式,此题得解.
四、作图题
12. (1)解:当x=0时,y=-2,即函数图象与y轴交点坐标为(0,-2),
当y=0时,x=-1,即函数图象与x轴交点坐标为(-1,0),
函数图象如图所示:
(2)解:由图可得:OA=1,OB=2,S△OAB= .
分析:(1)先求出函数与x、y轴的交点坐标,再过这两点画直线即可;(2)如图所示,先求得OA与OB的长度,再根据三角形面积公式进行计算即可.2·1·c·n·j·y
五、综合题
13. (1)解:设一次函数解析式为y=kx+b,
把(3,1),(2,0)代入得 ,解得 ,
所以一次函数解析式为y=x﹣2
(2)解:当x=6时,y=x﹣2=6﹣2=4.
分析:(1)利用待定系数法求一次函数解析式;(2)利用(1)中解析式计算自变量为6所对应的函数值即可.【来源:21·世纪·教育·网】
14. (1)解:设直线AB的解析式,
把点A(1,3),B(0,2)代入解析式得: ,
解得:k=1,b=2,
把k=1,b=2代入
得:y=x+2,
直线AB的解析式:y=x+2
(2)解:把y=0代入y=x+2得:x+2=0,
解得:x=﹣2,
∴点C的坐标为(﹣2,0),
∴OC=2,
∵△AOC的底为2,△AOC的高为点A的纵坐标3,
∴S△ABC=2×3× =3,
故三角形AOC的面积为3.
分析:(1)设直线AB的解析式为y=kx+b,把A、B的坐标代入求出k、b的值即可,(2)把y=0代入(1)所求出的解析式,便能求出C点坐标,从而利用三角形的面积公式求出三角形AOC的面积即可.21教育网
