初中数学人教版九年级下学期 第二十八章 28.1 锐角三角函数同步练习(含解析)
文档属性
| 名称 | 初中数学人教版九年级下学期 第二十八章 28.1 锐角三角函数同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 00:00:00 | ||
图片预览



文档简介
初中数学人教版九年级下学期 第二十八章 28.1 锐角三角函数
一、单选题
1.如图,在Rt△ABC中,∠C=90°,AC=4,AB=5,则sinB的值是(??? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
2.如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在E处,BE与AD相交于点F,下列结论:①BD=AD2+AB2;②△ABF≌△EDF;③ = 21·cn·jy·com
④AD=BD?cos45°.其中正确的一组是( ??)
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?①④?????????????????????????????????????D.?③④
3.如图, AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB= ,BD=5,则OH的长度为( ??)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.?1?????????????????????????????????????????D.?
4.在 中, , , ,则 的值为(??? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
5.已知△ABC中,∠C=90°,若AC= ,BC=1,则sinA的值是(?? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
6.已知:△ABC中,∠BCA=90°,CD⊥AB于D,若AD=1,AB=3,那么 的值是(?? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
二、填空题
7.计算sin60°tan60°- cos45°cos60°的结果为________?。
8.如图,已知直线l1∥l2∥l3∥l4 , 相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=________. 21世纪教育网版权所有
9.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是边AC的中点,点E,F在边AB上,当△DEF是等腰三角形,且底角的正切值是 时,△DEF腰长的值是________. www.21-cn-jy.com
三、计算题
10.2sin60°?tan45°+4cos230°﹣tan60°
先化简,再求代数式 ÷(1+ )的值,其中a=3tan30°+1.
四、解答题
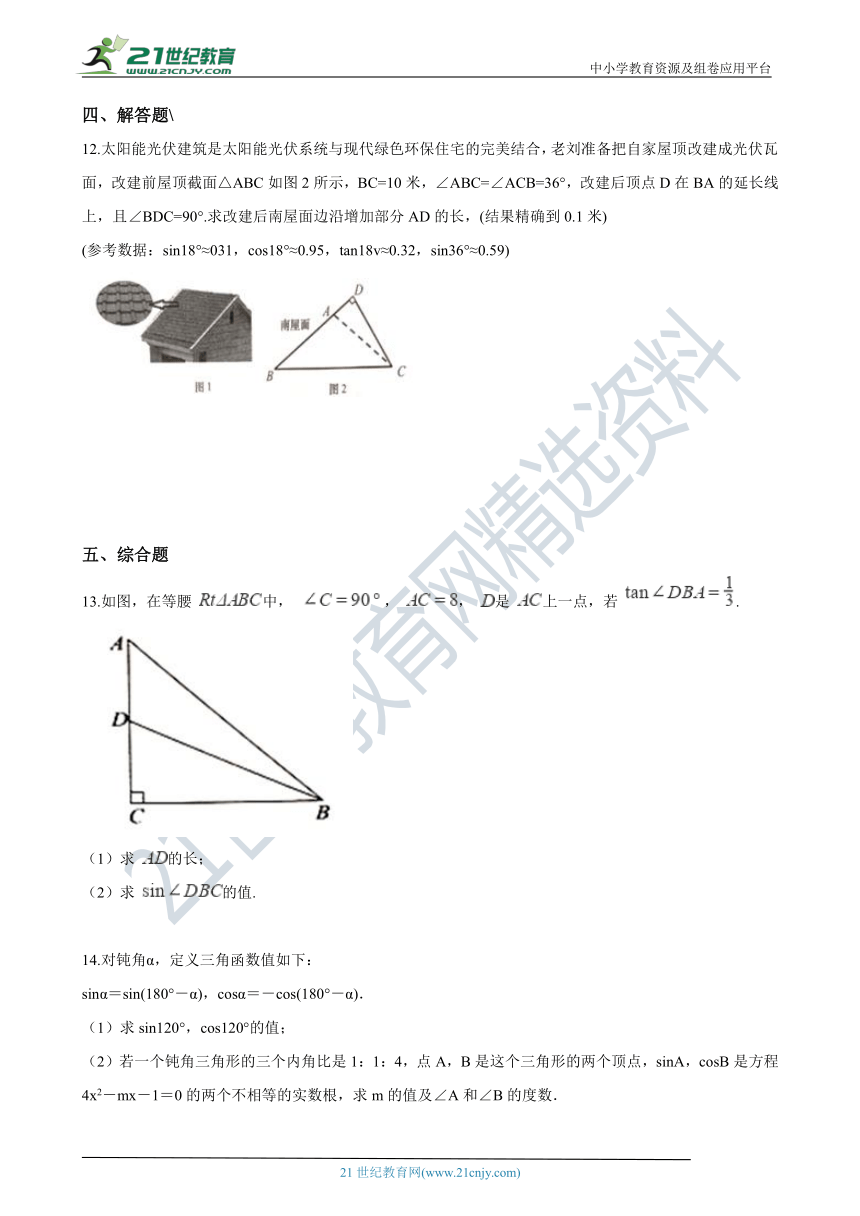
12.太阳能光伏建筑是太阳能光伏系统与现代绿色环保住宅的完美结合,老刘准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°.求改建后南屋面边沿增加部分AD的长,(结果精确到0.1米) 【来源:21cnj*y.co*m】
(参考数据:sin18°≈031,cos18°≈0.95,tan18v≈0.32,sin36°≈0.59)【出处:21教育名师】
五、综合题
13.如图,在等腰 中, , , 是 上一点,若 .
(1)求 的长;
(2)求 的值.
14.对钝角α,定义三角函数值如下:
sinα=sin(180°-α),cosα=-cos(180°-α).
(1)求sin120°,cos120°的值;
(2)若一个钝角三角形的三个内角比是1:1:4,点A,B是这个三角形的两个顶点,sinA,cosB是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A和∠B的度数. 21教育名师原创作品
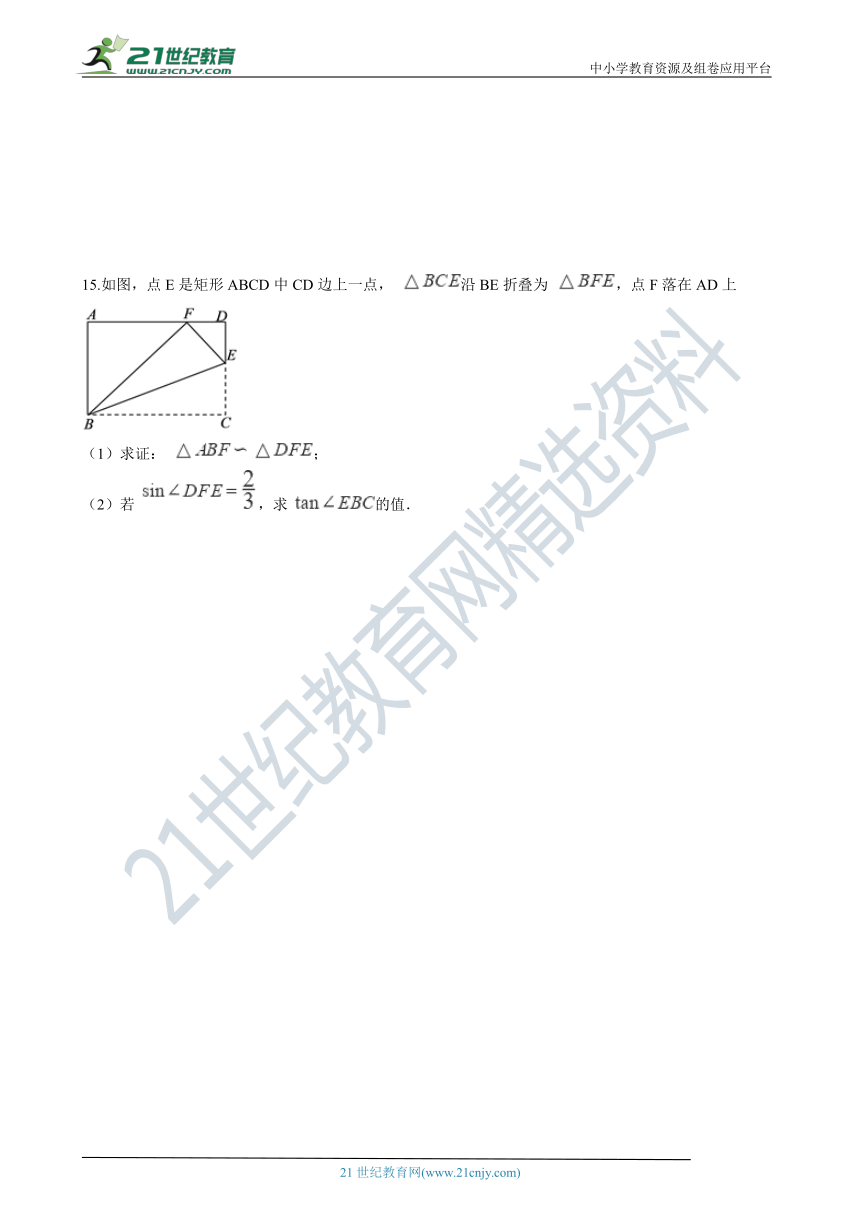
15.如图,点E是矩形ABCD中CD边上一点, 沿BE折叠为 ,点F落在AD上
(1)求证: ;
(2)若 ,求 的值.
答案解析部分
一、单选题
1. D
解: ∵在Rt△ABC中,∠C=90°,AC=4,AB=5, ∴ sinB=. 故答案为:D. 【来源:21·世纪·教育·网】
分析:根据正弦函数的定义sinB=即可直接得出答案.
2. B
①∵△ABD为直角三角形, ∴BD2=AD2+AB2? , ∴BD≠AD2+AB2 ,错误; ②根据折叠性质可知:DE=CD=AB,∠A=∠E,∠AFB=∠EFD,∴△ABF≌△EDF(AAS),正确; ③根据②可以得到△ABF≌△EDF,∴ = ?=1,正确; ④在Rt△ABD中,∠ADB≠45°,∴AD≠BD?cos45°,错误. 综上,正确的有 ?②③?. 故答案为:B. 分析:①由于△ABD为直角三角形,由勾股定理可得BD2=AD2+AB2;②根据矩形的性质结合折叠的性质DE=CD=AB,利用角角边定理可证△ABF≌△EDF;③由于△ABF≌△EDF,对应边之比等于1;④用三角函数的定义可得AD≠BD?cos45°.21cnjy.com
3. D
解:如解图,连接OD, ∵AB是⊙O的直径,点H是弦CD的中点,?? ∴由垂径定理可知AB⊥CD, 在Rt△BDH中, ∵cos∠CDB= ,BD=5, ∴DH=4,∴BH= = =3, 设OH=x,则OD=OB=x+3, 在Rt△ODH中,OD2=OH2+DH2 , ∴(x+3)2=x2+42 , 解得x= ,即OH= . 故答案为:D. 分析:连接OD,利用垂径定理可证得AB⊥CD,在Rt△BDH中,利用锐角三角函数的定义及勾股定理求出DH,BH的长,设OH=x,用含x的代数式表示出OD,再利用勾股定理建立关于x的方程,解方程求出x的值,即可得到OH的长。21·世纪*教育网
4. A
解:∵在Rt△ABC中,∠C=90°,AC=5,BC=12,
∴AB= =13,
则cosB= = ,
故答案为:A.
分析:利用锐角三角函数定义求出cosB的值即可.
5. C
在直角△ABC中,AB= =
则sinA= .
故答案为:C.
分析:在直角△ABC中首先利用勾股定理求得AB的长,然后利用正弦函数的定义求解.
6. D
解:∵CD⊥AB,
∴∠ACD=90°,
∴∠ACD=∠BAC,
又∵∠CAD=∠BAC,
∴△ACD∽△ABC,
∴ ,
即 ,
解得AC= ,
在Rt△ABC中,由勾股定理得, ,
所以,cosB= .
故答案为:D.
分析:先证明△ACD与△ABC相似,根据相似三角形对应边成比例求出AC,再利用勾股定理列式求出BC,然后根据锐角的余弦等于邻边比斜边列式即可.www-2-1-cnjy-com
二、填空题
7. 1
解:原式=×-×× =- =1 分析:根据特殊角的三角函数值进行计算即可得到答案。2·1·c·n·j·y
8.
解:过D作DF⊥l1, 交i2于点E, ∵∠ADF+∠CDE=∠CDE+∠DCE=90°, ∴∠ADF=∠DCE, ∵∠AFD=∠CED, ∵四边形ABCD是正方形, ∴AD=CD, ∴△AFD≌△DEC(AAS), ∴∴AF=DE=2, ∴AD=, ∴sin α ==. 故答案为:. 分析:过D作DF⊥l1, 交i2于点E,由同角的余角相等推得∠ADF=∠DCE,结合正方形的边长相等,利用角角边定理可证△AFD≌△DEC,则对应边AF=DE=2,于是在Rt△AFD中利用勾股定理即可求出AD的长,则sin α可求. ?21*cnjy*com
9. 或
∵∠C=90°,AC=4,BC=3,
∴AB= =5,
∵点D是边AC的中点,
∴AD= AC=2,作DM⊥AB于M,如图1所示:
∵sinA= = ,
即 = ,
∴DM= ,
分三种情况:
①当DE=DF时,
∵tan∠DFE= = ,
∴FM= DM= × = ,
∴DE=DF= = = ;
②当ED=EF时,作EN⊥DF于N,如图2所示:
由①得:DM= ,FM= ,DF= ;
∵EN⊥DF,∴FN=DN= DF= ,
∵tan∠EFD= = ,
∴EN= FN= ,
∴ED=EF= = ;
③当FE=FD时,作FG⊥DE于G,如图3所示:
则EG=DG,
同①得:EM= ,DE= ,
∴EG= ,
∵tan∠DEF= = ,
∴GF= EG= ,
∴EF= = ;
综上所述,当△DEF是等腰三角形,且底角的正切值是 时,△DEF腰长的值是 或 ;
故答案为: 或 .
分析:由勾股定理得出AB= =5,作DM⊥AB于M,由三角函数得出DM= ,分三种情况:①当DE=DF时,②当ED=EF时,作EN⊥DF于N,③当FE=FD时,作FG⊥DE于G;由等腰三角形的性质、三角函数定义和勾股定理即可得出答案.21教育网
三、计算题
10. 解:2sin60°?tan45°+4cos230°﹣tan60°
=2× ×1+4×( )2﹣
= +3﹣
=3.
分析:直接利用特殊角的三角函数值分别代入求出答案.
11. 解:原式=
=
= ,
当a=3tan30°+1=3× +1= +1时,原式= .
分析:先根据分式混合运算的法则把原式进行化简,再把a=3tan30°+1化简后代入进行计算即可.【版权所有:21教育】
四、解答题
12. 解:∵∠BDC=90°,BC=10, ,
∴ = ,
∵在Rt△BCD中,
∴ ,
∴在Rt△ACD中, ,
∴ = (米).
答:改建后南屋面边沿增加部分 的长约为1.9米。
分析:根据锐角三角函数的性质计算得到CD的长度,在直角三角形ACD中,根据锐角三角形函数的性质,即可得到AD的长度。21*cnjy*com
五、综合题
13. (1)解:过点 作 于点 ,
等腰三角形 , ,
,
设
,
由勾股定理可知: .
由勾股定理可知:
(2)解:由于 , ,
由勾股定理可知:
分析:(1) 过点 作 于点 ,求出AB的长,设 ,根据勾股定理即可求解.(2)由(1)得AD=4,由勾股定理求出DB的长,再根据三角函数的定义求解即可.
14. (1)解:
(2)解:三角形的三个内角的比是1:1:4,三个内角分别为30°,30°,120°,
①当∠A=30°,∠B=120°时,方程的两根为 ,
将 代入方程得: 解得:m=0,经检验 是方程 的根,m=0符合题意;
②当∠A=120°,∠B=30°时,两根为 ,不符合题意;
③当∠A=30°,∠B=30°时,两根为 ,将 代入方程得: 解得:m=0,经检验 不是方程4x2-1=0的根.2-1-c-n-j-y
综上所述:m=0,∠A=30°,∠B=120°
分析:(1)按照题目所给的信息求解即可;(2)分三种情况进行分析:①当∠A=30°,∠B=120°时;②当∠A=120°,∠B=30°时;③当∠A=30°,∠B=30°时,根据题意分别求出m的值即可.
15. (1)证明:∠A=∠D=900
在△
∴
∴∠ABF=∠DFE
∴
(2)解:在Rt△ ,
设
由折叠的性质知EF=EC,则AB=DC=5
由 ,得
故
分析:(1)根据矩形的性质可知∠A=∠D=∠C=90°,△BCE沿BE折叠为△BFE,得出∠BFE=∠C=90°,再根据三角形的内角和为180°,可知∠AFB+∠ABF=90°,得出∠ABF=∠DFE,即可证明△ABF∽△DFE;(2)已知 ,设DE=2a,EF=3a,DF= a,由折叠的性质知EF=EC,则BC=DC= 由 ,得 即可得到 .
一、单选题
1.如图,在Rt△ABC中,∠C=90°,AC=4,AB=5,则sinB的值是(??? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
2.如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在E处,BE与AD相交于点F,下列结论:①BD=AD2+AB2;②△ABF≌△EDF;③ = 21·cn·jy·com
④AD=BD?cos45°.其中正确的一组是( ??)
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?①④?????????????????????????????????????D.?③④
3.如图, AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB= ,BD=5,则OH的长度为( ??)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.?1?????????????????????????????????????????D.?
4.在 中, , , ,则 的值为(??? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
5.已知△ABC中,∠C=90°,若AC= ,BC=1,则sinA的值是(?? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
6.已知:△ABC中,∠BCA=90°,CD⊥AB于D,若AD=1,AB=3,那么 的值是(?? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
二、填空题
7.计算sin60°tan60°- cos45°cos60°的结果为________?。
8.如图,已知直线l1∥l2∥l3∥l4 , 相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=________. 21世纪教育网版权所有
9.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是边AC的中点,点E,F在边AB上,当△DEF是等腰三角形,且底角的正切值是 时,△DEF腰长的值是________. www.21-cn-jy.com
三、计算题
10.2sin60°?tan45°+4cos230°﹣tan60°
先化简,再求代数式 ÷(1+ )的值,其中a=3tan30°+1.
四、解答题
12.太阳能光伏建筑是太阳能光伏系统与现代绿色环保住宅的完美结合,老刘准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°.求改建后南屋面边沿增加部分AD的长,(结果精确到0.1米) 【来源:21cnj*y.co*m】
(参考数据:sin18°≈031,cos18°≈0.95,tan18v≈0.32,sin36°≈0.59)【出处:21教育名师】
五、综合题
13.如图,在等腰 中, , , 是 上一点,若 .
(1)求 的长;
(2)求 的值.
14.对钝角α,定义三角函数值如下:
sinα=sin(180°-α),cosα=-cos(180°-α).
(1)求sin120°,cos120°的值;
(2)若一个钝角三角形的三个内角比是1:1:4,点A,B是这个三角形的两个顶点,sinA,cosB是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A和∠B的度数. 21教育名师原创作品
15.如图,点E是矩形ABCD中CD边上一点, 沿BE折叠为 ,点F落在AD上
(1)求证: ;
(2)若 ,求 的值.
答案解析部分
一、单选题
1. D
解: ∵在Rt△ABC中,∠C=90°,AC=4,AB=5, ∴ sinB=. 故答案为:D. 【来源:21·世纪·教育·网】
分析:根据正弦函数的定义sinB=即可直接得出答案.
2. B
①∵△ABD为直角三角形, ∴BD2=AD2+AB2? , ∴BD≠AD2+AB2 ,错误; ②根据折叠性质可知:DE=CD=AB,∠A=∠E,∠AFB=∠EFD,∴△ABF≌△EDF(AAS),正确; ③根据②可以得到△ABF≌△EDF,∴ = ?=1,正确; ④在Rt△ABD中,∠ADB≠45°,∴AD≠BD?cos45°,错误. 综上,正确的有 ?②③?. 故答案为:B. 分析:①由于△ABD为直角三角形,由勾股定理可得BD2=AD2+AB2;②根据矩形的性质结合折叠的性质DE=CD=AB,利用角角边定理可证△ABF≌△EDF;③由于△ABF≌△EDF,对应边之比等于1;④用三角函数的定义可得AD≠BD?cos45°.21cnjy.com
3. D
解:如解图,连接OD, ∵AB是⊙O的直径,点H是弦CD的中点,?? ∴由垂径定理可知AB⊥CD, 在Rt△BDH中, ∵cos∠CDB= ,BD=5, ∴DH=4,∴BH= = =3, 设OH=x,则OD=OB=x+3, 在Rt△ODH中,OD2=OH2+DH2 , ∴(x+3)2=x2+42 , 解得x= ,即OH= . 故答案为:D. 分析:连接OD,利用垂径定理可证得AB⊥CD,在Rt△BDH中,利用锐角三角函数的定义及勾股定理求出DH,BH的长,设OH=x,用含x的代数式表示出OD,再利用勾股定理建立关于x的方程,解方程求出x的值,即可得到OH的长。21·世纪*教育网
4. A
解:∵在Rt△ABC中,∠C=90°,AC=5,BC=12,
∴AB= =13,
则cosB= = ,
故答案为:A.
分析:利用锐角三角函数定义求出cosB的值即可.
5. C
在直角△ABC中,AB= =
则sinA= .
故答案为:C.
分析:在直角△ABC中首先利用勾股定理求得AB的长,然后利用正弦函数的定义求解.
6. D
解:∵CD⊥AB,
∴∠ACD=90°,
∴∠ACD=∠BAC,
又∵∠CAD=∠BAC,
∴△ACD∽△ABC,
∴ ,
即 ,
解得AC= ,
在Rt△ABC中,由勾股定理得, ,
所以,cosB= .
故答案为:D.
分析:先证明△ACD与△ABC相似,根据相似三角形对应边成比例求出AC,再利用勾股定理列式求出BC,然后根据锐角的余弦等于邻边比斜边列式即可.www-2-1-cnjy-com
二、填空题
7. 1
解:原式=×-×× =- =1 分析:根据特殊角的三角函数值进行计算即可得到答案。2·1·c·n·j·y
8.
解:过D作DF⊥l1, 交i2于点E, ∵∠ADF+∠CDE=∠CDE+∠DCE=90°, ∴∠ADF=∠DCE, ∵∠AFD=∠CED, ∵四边形ABCD是正方形, ∴AD=CD, ∴△AFD≌△DEC(AAS), ∴∴AF=DE=2, ∴AD=, ∴sin α ==. 故答案为:. 分析:过D作DF⊥l1, 交i2于点E,由同角的余角相等推得∠ADF=∠DCE,结合正方形的边长相等,利用角角边定理可证△AFD≌△DEC,则对应边AF=DE=2,于是在Rt△AFD中利用勾股定理即可求出AD的长,则sin α可求. ?21*cnjy*com
9. 或
∵∠C=90°,AC=4,BC=3,
∴AB= =5,
∵点D是边AC的中点,
∴AD= AC=2,作DM⊥AB于M,如图1所示:
∵sinA= = ,
即 = ,
∴DM= ,
分三种情况:
①当DE=DF时,
∵tan∠DFE= = ,
∴FM= DM= × = ,
∴DE=DF= = = ;
②当ED=EF时,作EN⊥DF于N,如图2所示:
由①得:DM= ,FM= ,DF= ;
∵EN⊥DF,∴FN=DN= DF= ,
∵tan∠EFD= = ,
∴EN= FN= ,
∴ED=EF= = ;
③当FE=FD时,作FG⊥DE于G,如图3所示:
则EG=DG,
同①得:EM= ,DE= ,
∴EG= ,
∵tan∠DEF= = ,
∴GF= EG= ,
∴EF= = ;
综上所述,当△DEF是等腰三角形,且底角的正切值是 时,△DEF腰长的值是 或 ;
故答案为: 或 .
分析:由勾股定理得出AB= =5,作DM⊥AB于M,由三角函数得出DM= ,分三种情况:①当DE=DF时,②当ED=EF时,作EN⊥DF于N,③当FE=FD时,作FG⊥DE于G;由等腰三角形的性质、三角函数定义和勾股定理即可得出答案.21教育网
三、计算题
10. 解:2sin60°?tan45°+4cos230°﹣tan60°
=2× ×1+4×( )2﹣
= +3﹣
=3.
分析:直接利用特殊角的三角函数值分别代入求出答案.
11. 解:原式=
=
= ,
当a=3tan30°+1=3× +1= +1时,原式= .
分析:先根据分式混合运算的法则把原式进行化简,再把a=3tan30°+1化简后代入进行计算即可.【版权所有:21教育】
四、解答题
12. 解:∵∠BDC=90°,BC=10, ,
∴ = ,
∵在Rt△BCD中,
∴ ,
∴在Rt△ACD中, ,
∴ = (米).
答:改建后南屋面边沿增加部分 的长约为1.9米。
分析:根据锐角三角函数的性质计算得到CD的长度,在直角三角形ACD中,根据锐角三角形函数的性质,即可得到AD的长度。21*cnjy*com
五、综合题
13. (1)解:过点 作 于点 ,
等腰三角形 , ,
,
设
,
由勾股定理可知: .
由勾股定理可知:
(2)解:由于 , ,
由勾股定理可知:
分析:(1) 过点 作 于点 ,求出AB的长,设 ,根据勾股定理即可求解.(2)由(1)得AD=4,由勾股定理求出DB的长,再根据三角函数的定义求解即可.
14. (1)解:
(2)解:三角形的三个内角的比是1:1:4,三个内角分别为30°,30°,120°,
①当∠A=30°,∠B=120°时,方程的两根为 ,
将 代入方程得: 解得:m=0,经检验 是方程 的根,m=0符合题意;
②当∠A=120°,∠B=30°时,两根为 ,不符合题意;
③当∠A=30°,∠B=30°时,两根为 ,将 代入方程得: 解得:m=0,经检验 不是方程4x2-1=0的根.2-1-c-n-j-y
综上所述:m=0,∠A=30°,∠B=120°
分析:(1)按照题目所给的信息求解即可;(2)分三种情况进行分析:①当∠A=30°,∠B=120°时;②当∠A=120°,∠B=30°时;③当∠A=30°,∠B=30°时,根据题意分别求出m的值即可.
15. (1)证明:∠A=∠D=900
在△
∴
∴∠ABF=∠DFE
∴
(2)解:在Rt△ ,
设
由折叠的性质知EF=EC,则AB=DC=5
由 ,得
故
分析:(1)根据矩形的性质可知∠A=∠D=∠C=90°,△BCE沿BE折叠为△BFE,得出∠BFE=∠C=90°,再根据三角形的内角和为180°,可知∠AFB+∠ABF=90°,得出∠ABF=∠DFE,即可证明△ABF∽△DFE;(2)已知 ,设DE=2a,EF=3a,DF= a,由折叠的性质知EF=EC,则BC=DC= 由 ,得 即可得到 .
