初中数学人教版九年级下学期 第二十九章 投影与视图 单元测试卷(含解析)
文档属性
| 名称 | 初中数学人教版九年级下学期 第二十九章 投影与视图 单元测试卷(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 00:00:00 | ||
图片预览



文档简介
初中数学人教版九年级下学期 第二十九章测试卷
一、单选题
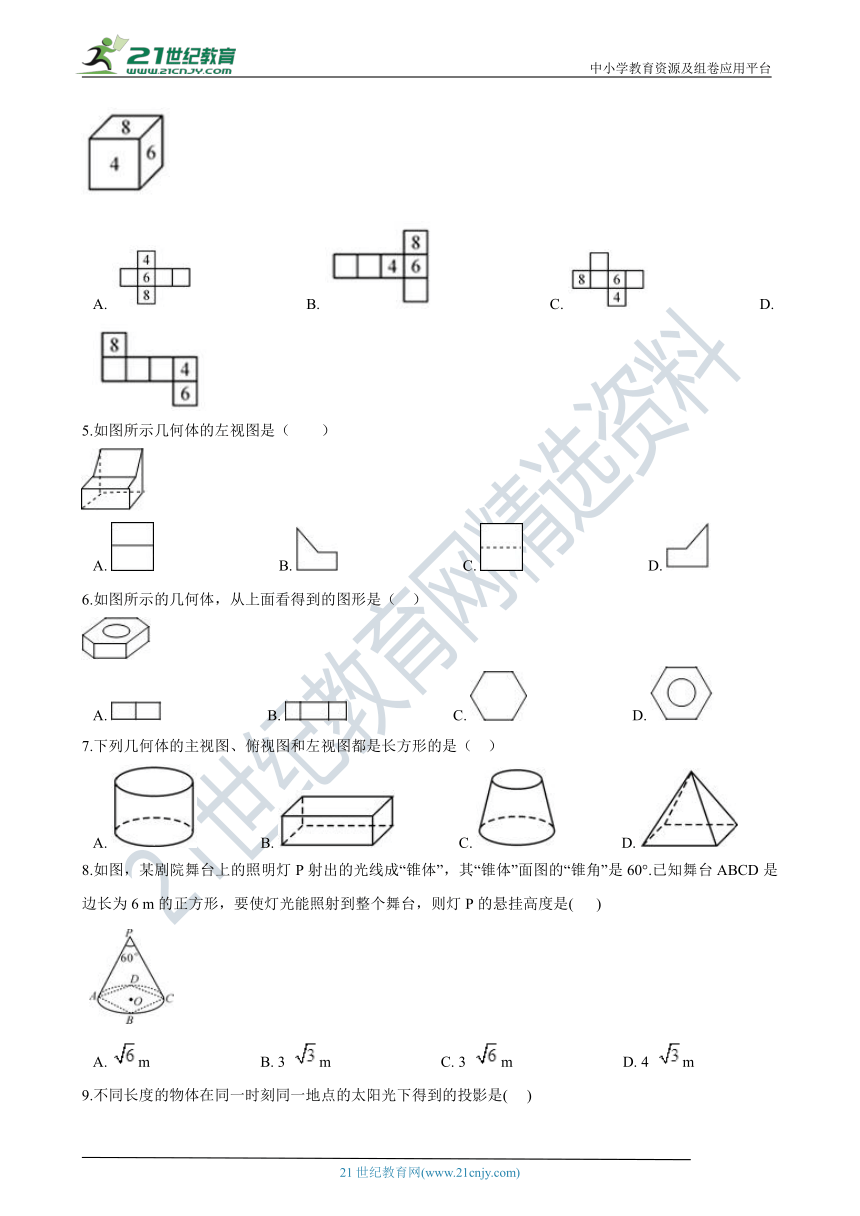
1.如图是一个正方体的表面展开图,若正方体中相对的面上的数互为相反数,则2x﹣y的值为(?? )
A.?-2????????????????????????????????????????B.?6????????????????????????????????????????C.?????????????????????????????????????????D.?2
2.已知某多面体的平面展开图如图所示,其中是三棱柱的有(???? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
3.用4个棱长为1的正方体搭成一个几何体模型,其主视图与左视图如图所示,则该立方体的俯视图不可能是( ??) www.21-cn-jy.com
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?【版权所有:21教育】
4.如图是一个表面写有数字的正方体,其表面展开图可能是(??? )
A.???????????????????????B.???????????????????????C.???????????????????????D.?21教育名师原创作品
5.如图所示几何体的左视图是( )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
6.如图所示的几何体,从上面看得到的图形是(?? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
7.下列几何体的主视图、俯视图和左视图都是长方形的是( ??)
A.??????????????????B.??????????????????C.??????????????????D.?
8.如图,某剧院舞台上的照明灯P射出的光线成“锥体”,其“锥体”面图的“锥角”是60°.已知舞台ABCD是边长为6 m的正方形,要使灯光能照射到整个舞台,则灯P的悬挂高度是(???? ) 【来源:21·世纪·教育·网】
A.?m?????????????????????????????B.?3 m?????????????????????????????C.?3 m?????????????????????????????D.?4 m
9.不同长度的物体在同一时刻同一地点的太阳光下得到的投影是(??? )
A.?相等??????????????????????????????B.?长的较长??????????????????????????????C.?短的较长??????????????????????????????D.?不能确定
10.下列现象属于中心投影的有(?? )
①小孔成像; ②皮影戏;③手影; ④放电影.
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
11.下列投影中,投射线与投影面垂直的有(?? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题
12.小明的身高为1.6米,他在阳光下的影长为0.8米,同一时刻,测得校园的旗杆的影长为4.5米,则该旗杆的高为________米. 21*cnjy*com
13.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为________cm.
三、综合题
14.如图是一个正方体的平面展开图,标注了字母M的是正方体的正面,如果正方体的左面与右面标注的式子相等.
(1)求x的值;
(2)求正方体的上面和底面的数字和.
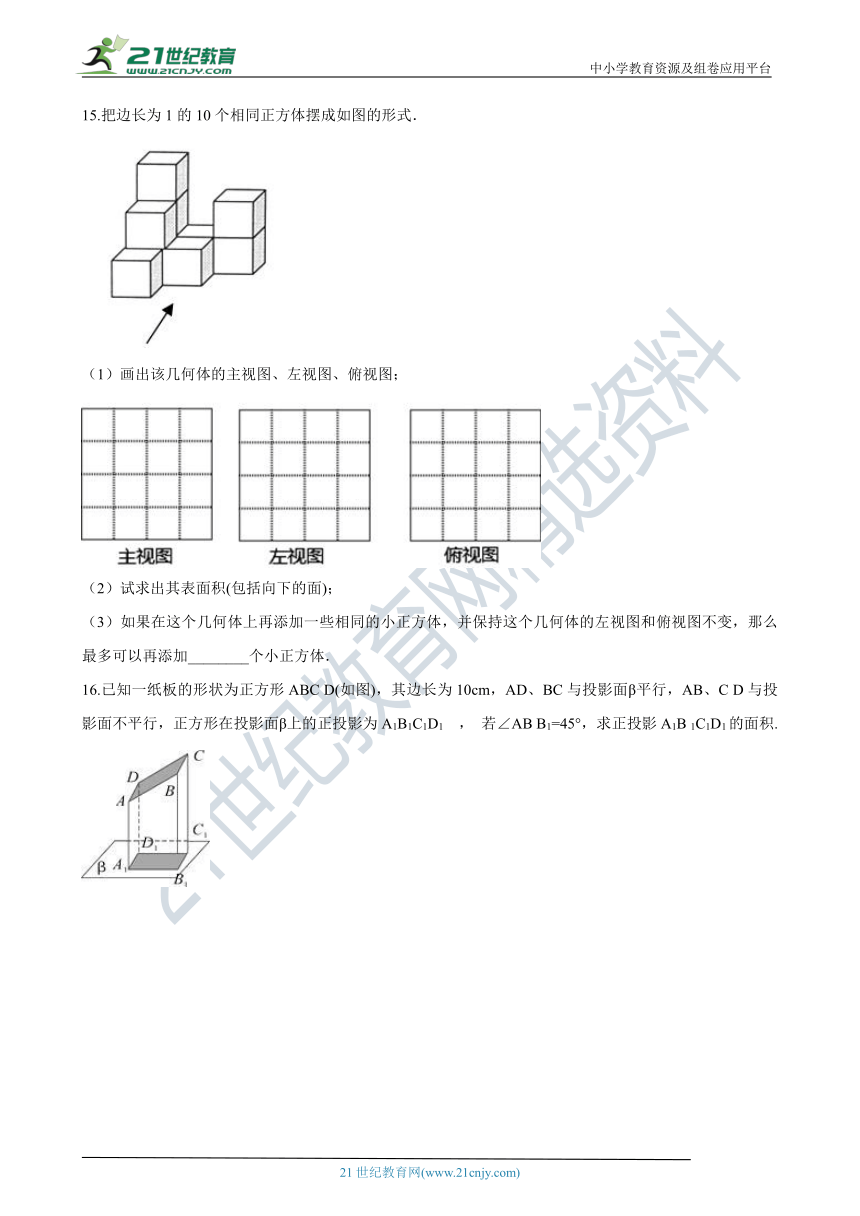
15.把边长为1的10个相同正方体摆成如图的形式.
(1)画出该几何体的主视图、左视图、俯视图;
(2)试求出其表面积(包括向下的面);
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加________个小正方体.
16.已知一纸板的形状为正方形ABC D(如图),其边长为10cm,AD、BC与投影面β平行,AB、C D与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1 , 若∠AB B1=45°,求正投影A1B 1C1D1的面积.
答案解析部分
一、单选题
1. B
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“x”与“y”是相对面,
“5”与“-5”是相对面,
“-4”与“3x-2”是相对面,
∵相对面上所标的两个数互为相反数,
∴3x-2+(-4)=0,
x+y=0,
解得x=2,y=-2.
∴2x﹣y=6.
故答案为:B.
分析正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点确定出相对面,再求出x、y、z的值,然后代入代数式计算即可得解.21教育网
2. B
从图中左边第一个是三棱锥;
第二个是三棱柱;
第三个是四棱锥;
第四个是三棱柱,
故答案为:B.
分析根据已知图形和多面体的特点分析各图案的能围成的几何体,熟记三棱锥、三棱柱的定义与区别解答.
3. D
解:由主视图可得此组合几何体有两列,左边第一列出现2层;由左视图可得此组合几何体有2行,从上面第一行出现2层,综上所述可得左边数第一列,上面数第一行小正方体的个数一定是2个,选项中只有D的是1个,故答案为:D. 21·世纪*教育网
分析主视图和左视图将决定组合几何体的层数,列数及行数.
4. B
解:根据原正方体可得标有数字4,6,8三个面为邻面,不是对面关系,而A选项展开图标有数字4,8两面为对面关系,C选项展开图标有数字6,8两面为对面关系,D选项展开图标有数字6,8两面为对面关系,B选项展开图符合原正方体,是正方体的展开图. 21cnjy.com
故答案为:B
分析根据正方体的展开图相隔一个正方形是对面关系判断即可.
5. B
从左边看是:
故答案为:B.
分析根据左视图是从左边看得到的图形,可得答案.
6. D
解:从上边往下看为:正六边形,中间有一个圆,如图所示:
故答案为:D.
分析根据从上边看得到的图形是俯视图,即可可得答案.
7. B
解:A、主视图和左视图为矩形,俯视图为圆,故答案为:错误,不符合题意;
B、主视图为矩形,俯视图和左视图都为矩形,故答案为:正确,符合题意;
C、主视图和左视图为等腰梯形,俯视图为圆环,故答案为:错误,不符合题意;
D、主视图和左视图为三角形,俯视图为有对角线的矩形,故答案为:错误,不符合题意.
故答案为:B.
分析主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的正投影,找到各个几何体的三视图即可作出判断.21世纪教育网版权所有
8.C
解:连接AC,
∵∠APC=60°,
∴∠PAC=∠PCA=60°,
∵ABCD是边长为6m的正方形,
∴AC=6 ,OC=3
∴PC=6 ,
∴PO=3 ,
故答案为:C
分析连接AC,根据圆锥体的性质及∠APC=60°,可以判断出三角形PAC是一个等边三角形,根据正方形的性质利用勾股定理算出AC的长,进而得出OC的长,根据圆锥的高,母线,底面圆的半径刚好围成一个直角三角形,利用勾股定理即可算出PO的长。21·cn·jy·com
9. D
解:在同一时刻,同一地点, 不同长度的物体所摆放的相对位置不确定, 所以无法比较物体投影的长度. 故答案为D。2·1·c·n·j·y
分析由于一个物体在一个地点相对地面的位置不同,投影的长度也不一定相同,更何况不同长度的物体,据此分析即可。www-2-1-cnjy-com
10.D
解:根据中心投影的定义可知答案为:D, 故答案为:D.
分析中心投影:若一束光线是从一点发出的,像这样的光线照射在物体上所形成的投影,叫做中心投影。这个“点”就是中心,生活中能形成中心投影的点光源主要有手电筒、路灯、台灯、投影仪的灯光、放映机的灯光等。由此可得出答案.2-1-c-n-j-y
11. B
解:依题可得:图三,图四是投射线与投影面垂直, 故答案为:B.
分析垂直投影:按y轴方向的投影,由此定义一一分析即可得出答案.
二、填空题
12. 9
设旗杆为xm,根据题意得:
,
解得:x=9.
所以旗杆为9米.
故答案为:9.
分析设旗杆为xm,根据在同一时刻物高与影长的比相等得到 ,然后利用比例性质求出x即可.
13.18
如图,
∵DE∥BC,∴△AED∽△ABC,∴ ,设屏幕上的小树高是x,则 ,解得x=18cm.故答案为:18.21*cnjy*com
分析根据实际情景抽象出数学图形,很容易证出△AED∽△ABC,根据相似三角形的对应边成比例即可建立方程,求解即可。【来源:21cnj*y.co*m】
三、综合题
14. (1)解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“M”与“x”是相对面,
“-2”与“-3”是相对面,
“4x”与“2x+3”是相对面,
∵正方体的左面与右面标注的式子相等,
∴4x=2x+3,
解得x=1.5
(2)解:∵标注了A字母的是正方体的正面,左面与右面标注的式子相等,
∴上面和底面上的两个数字-2和-3,
∴-2-3=-5.
分析(1)正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,然后列出方程求解即可;(2)确定出上面和底面上的两个数字-2和-3,然后相加即可.【出处:21教育名师】
15. (1)如图所示: (2)解:表面积为:6×2+6×2+6×2+2=38; (3)4
解:(3)最多可以添加4个小小正方体. 故答案为:4. 分析(1)直接利用三视图的画法进而得出答案; (2)利用几何体的形状进而得出其表面积; (3)利用左视图和俯视图不变,得出可以添加的位置.
16.解:过A作AEBB1 , 交于点E, 因为∠ABB1=45°, 所以AE=BE=cm 因为四边形ABCD是正方形,AD、BC与投影面β平行, 所以A1D1=B1C1=AD=BC=10cm, 所以正投影A1B 1C1D1的面积=10×=(cm2)
分析AD、BC与投影面β平行,则A1D1=B1C1=AD=BC,而且四边形ABCD是正方形,可得正投影A1B 1C1D1是正方形,求出A1B1的长即可(根据∠ABB1=45°可求得)。
一、单选题
1.如图是一个正方体的表面展开图,若正方体中相对的面上的数互为相反数,则2x﹣y的值为(?? )
A.?-2????????????????????????????????????????B.?6????????????????????????????????????????C.?????????????????????????????????????????D.?2
2.已知某多面体的平面展开图如图所示,其中是三棱柱的有(???? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
3.用4个棱长为1的正方体搭成一个几何体模型,其主视图与左视图如图所示,则该立方体的俯视图不可能是( ??) www.21-cn-jy.com
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?【版权所有:21教育】
4.如图是一个表面写有数字的正方体,其表面展开图可能是(??? )
A.???????????????????????B.???????????????????????C.???????????????????????D.?21教育名师原创作品
5.如图所示几何体的左视图是( )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
6.如图所示的几何体,从上面看得到的图形是(?? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
7.下列几何体的主视图、俯视图和左视图都是长方形的是( ??)
A.??????????????????B.??????????????????C.??????????????????D.?
8.如图,某剧院舞台上的照明灯P射出的光线成“锥体”,其“锥体”面图的“锥角”是60°.已知舞台ABCD是边长为6 m的正方形,要使灯光能照射到整个舞台,则灯P的悬挂高度是(???? ) 【来源:21·世纪·教育·网】
A.?m?????????????????????????????B.?3 m?????????????????????????????C.?3 m?????????????????????????????D.?4 m
9.不同长度的物体在同一时刻同一地点的太阳光下得到的投影是(??? )
A.?相等??????????????????????????????B.?长的较长??????????????????????????????C.?短的较长??????????????????????????????D.?不能确定
10.下列现象属于中心投影的有(?? )
①小孔成像; ②皮影戏;③手影; ④放电影.
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
11.下列投影中,投射线与投影面垂直的有(?? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题
12.小明的身高为1.6米,他在阳光下的影长为0.8米,同一时刻,测得校园的旗杆的影长为4.5米,则该旗杆的高为________米. 21*cnjy*com
13.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为________cm.
三、综合题
14.如图是一个正方体的平面展开图,标注了字母M的是正方体的正面,如果正方体的左面与右面标注的式子相等.
(1)求x的值;
(2)求正方体的上面和底面的数字和.
15.把边长为1的10个相同正方体摆成如图的形式.
(1)画出该几何体的主视图、左视图、俯视图;
(2)试求出其表面积(包括向下的面);
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加________个小正方体.
16.已知一纸板的形状为正方形ABC D(如图),其边长为10cm,AD、BC与投影面β平行,AB、C D与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1 , 若∠AB B1=45°,求正投影A1B 1C1D1的面积.
答案解析部分
一、单选题
1. B
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“x”与“y”是相对面,
“5”与“-5”是相对面,
“-4”与“3x-2”是相对面,
∵相对面上所标的两个数互为相反数,
∴3x-2+(-4)=0,
x+y=0,
解得x=2,y=-2.
∴2x﹣y=6.
故答案为:B.
分析正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点确定出相对面,再求出x、y、z的值,然后代入代数式计算即可得解.21教育网
2. B
从图中左边第一个是三棱锥;
第二个是三棱柱;
第三个是四棱锥;
第四个是三棱柱,
故答案为:B.
分析根据已知图形和多面体的特点分析各图案的能围成的几何体,熟记三棱锥、三棱柱的定义与区别解答.
3. D
解:由主视图可得此组合几何体有两列,左边第一列出现2层;由左视图可得此组合几何体有2行,从上面第一行出现2层,综上所述可得左边数第一列,上面数第一行小正方体的个数一定是2个,选项中只有D的是1个,故答案为:D. 21·世纪*教育网
分析主视图和左视图将决定组合几何体的层数,列数及行数.
4. B
解:根据原正方体可得标有数字4,6,8三个面为邻面,不是对面关系,而A选项展开图标有数字4,8两面为对面关系,C选项展开图标有数字6,8两面为对面关系,D选项展开图标有数字6,8两面为对面关系,B选项展开图符合原正方体,是正方体的展开图. 21cnjy.com
故答案为:B
分析根据正方体的展开图相隔一个正方形是对面关系判断即可.
5. B
从左边看是:
故答案为:B.
分析根据左视图是从左边看得到的图形,可得答案.
6. D
解:从上边往下看为:正六边形,中间有一个圆,如图所示:
故答案为:D.
分析根据从上边看得到的图形是俯视图,即可可得答案.
7. B
解:A、主视图和左视图为矩形,俯视图为圆,故答案为:错误,不符合题意;
B、主视图为矩形,俯视图和左视图都为矩形,故答案为:正确,符合题意;
C、主视图和左视图为等腰梯形,俯视图为圆环,故答案为:错误,不符合题意;
D、主视图和左视图为三角形,俯视图为有对角线的矩形,故答案为:错误,不符合题意.
故答案为:B.
分析主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的正投影,找到各个几何体的三视图即可作出判断.21世纪教育网版权所有
8.C
解:连接AC,
∵∠APC=60°,
∴∠PAC=∠PCA=60°,
∵ABCD是边长为6m的正方形,
∴AC=6 ,OC=3
∴PC=6 ,
∴PO=3 ,
故答案为:C
分析连接AC,根据圆锥体的性质及∠APC=60°,可以判断出三角形PAC是一个等边三角形,根据正方形的性质利用勾股定理算出AC的长,进而得出OC的长,根据圆锥的高,母线,底面圆的半径刚好围成一个直角三角形,利用勾股定理即可算出PO的长。21·cn·jy·com
9. D
解:在同一时刻,同一地点, 不同长度的物体所摆放的相对位置不确定, 所以无法比较物体投影的长度. 故答案为D。2·1·c·n·j·y
分析由于一个物体在一个地点相对地面的位置不同,投影的长度也不一定相同,更何况不同长度的物体,据此分析即可。www-2-1-cnjy-com
10.D
解:根据中心投影的定义可知答案为:D, 故答案为:D.
分析中心投影:若一束光线是从一点发出的,像这样的光线照射在物体上所形成的投影,叫做中心投影。这个“点”就是中心,生活中能形成中心投影的点光源主要有手电筒、路灯、台灯、投影仪的灯光、放映机的灯光等。由此可得出答案.2-1-c-n-j-y
11. B
解:依题可得:图三,图四是投射线与投影面垂直, 故答案为:B.
分析垂直投影:按y轴方向的投影,由此定义一一分析即可得出答案.
二、填空题
12. 9
设旗杆为xm,根据题意得:
,
解得:x=9.
所以旗杆为9米.
故答案为:9.
分析设旗杆为xm,根据在同一时刻物高与影长的比相等得到 ,然后利用比例性质求出x即可.
13.18
如图,
∵DE∥BC,∴△AED∽△ABC,∴ ,设屏幕上的小树高是x,则 ,解得x=18cm.故答案为:18.21*cnjy*com
分析根据实际情景抽象出数学图形,很容易证出△AED∽△ABC,根据相似三角形的对应边成比例即可建立方程,求解即可。【来源:21cnj*y.co*m】
三、综合题
14. (1)解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“M”与“x”是相对面,
“-2”与“-3”是相对面,
“4x”与“2x+3”是相对面,
∵正方体的左面与右面标注的式子相等,
∴4x=2x+3,
解得x=1.5
(2)解:∵标注了A字母的是正方体的正面,左面与右面标注的式子相等,
∴上面和底面上的两个数字-2和-3,
∴-2-3=-5.
分析(1)正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,然后列出方程求解即可;(2)确定出上面和底面上的两个数字-2和-3,然后相加即可.【出处:21教育名师】
15. (1)如图所示: (2)解:表面积为:6×2+6×2+6×2+2=38; (3)4
解:(3)最多可以添加4个小小正方体. 故答案为:4. 分析(1)直接利用三视图的画法进而得出答案; (2)利用几何体的形状进而得出其表面积; (3)利用左视图和俯视图不变,得出可以添加的位置.
16.解:过A作AEBB1 , 交于点E, 因为∠ABB1=45°, 所以AE=BE=cm 因为四边形ABCD是正方形,AD、BC与投影面β平行, 所以A1D1=B1C1=AD=BC=10cm, 所以正投影A1B 1C1D1的面积=10×=(cm2)
分析AD、BC与投影面β平行,则A1D1=B1C1=AD=BC,而且四边形ABCD是正方形,可得正投影A1B 1C1D1是正方形,求出A1B1的长即可(根据∠ABB1=45°可求得)。
