2020春北师大版八下数学4.2提公因式法教学课件(共21张)
文档属性
| 名称 | 2020春北师大版八下数学4.2提公因式法教学课件(共21张) |  | |
| 格式 | zip | ||
| 文件大小 | 197.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-01 18:19:55 | ||
图片预览







文档简介
课件21张PPT。4.2提公因式法
请把下列多项式写成整式的乘积的形式:
(1) x2+x=______;
(2)x2 – 1= ________.x(x+1)(x+1)(x-1) 像上面我们把一个多项式化成几个整式的乘积的形式,这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.回顾
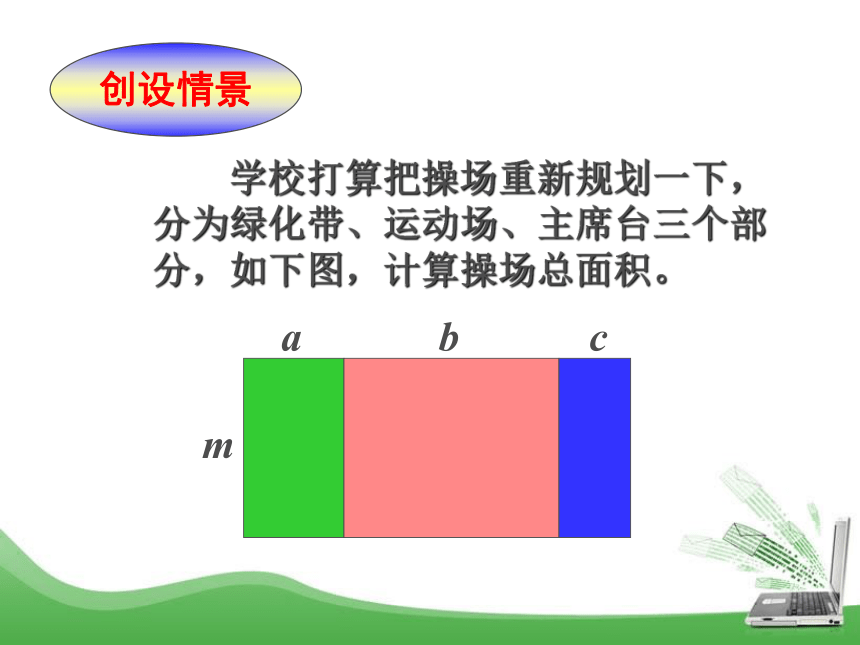
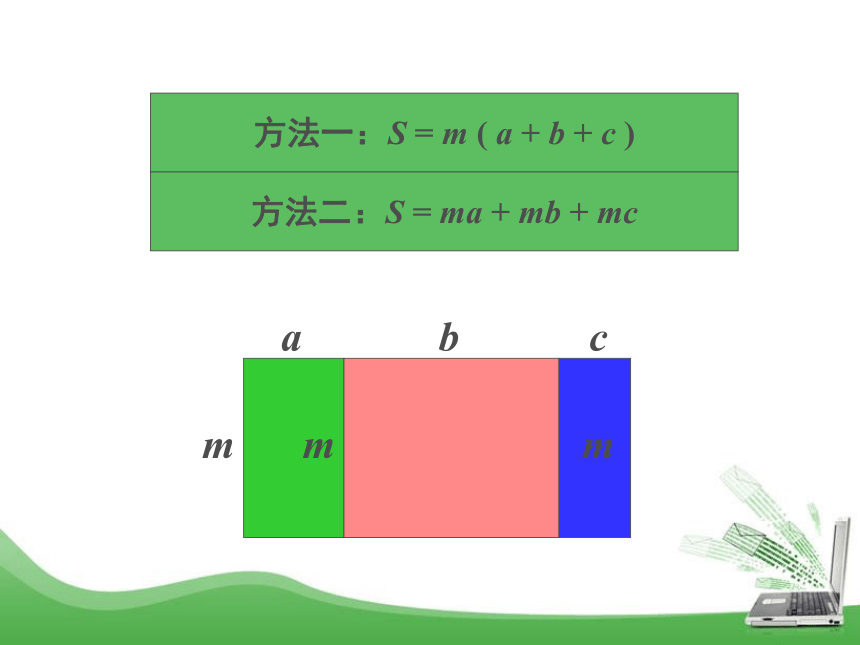
(3) a2- b2 =(a + b) (a-b) (a+b) (a-b)a2 - b2整式乘法因式分解因式分解和整式乘法是相反方向的变形:a2+2ab+b2(a+b)2因式分解整式乘法深入理解创设情景 学校打算把操场重新规划一下,分为绿化带、运动场、主席台三个部分,如下图,计算操场总面积。abcm方法一:S = m ( a + b + c )方法二:S = ma + mb + mcmm方法一:S = m ( a + b + c )方法二:S = ma + mb + mc 在式子ma + mb + mc中,m是这个多项式中每一个项都含有的相同因式,叫做 。公因式ma + mb + mc = m ( a + b + c )如果多项式的各项有公因式,可以把这个公因式提出来,将多项式写成公因式与另一个因式的乘积的形式。这种分解因式的方法叫做提公因式法。提公因式法:提公因式法的一般步骤 :1、确定公因式; 2、提取公因式。将原多项式式除以公因式,得到一个新多项式,归纳总结ma + mb + mc = m ( a + b + c )3、把新多项式与公因式相乘。议一议中各项的公因式是什么? ①多项式②你能尝试将多项式因式分解吗?③多项式 中各项的公因式是什么?
你认为怎样确定一个多项式的公因式?结论:(1)各项系数是整数,系数的最大公约数是公因式的系数;
(2)各项都含有的字母的最低次幂的积是公因式的字母部分;
(3)公因式的系数与公因式字母部分的积是这个多项式的公因式. 正确找出多项式各项公因式的关键是什么?1、定系数:公因式的系数是多项式各项系数 的最大公约数。 2、定字母:字母取多项式中各项都含有的相同字母。
3、定指数:指数取相同字母指数的最低次幂.
4、多项式各项的公因式可以是单项式,也 可以是多项式.例: 找 3 x 2 – 6 x 的公因式。系数:最大
公约数。3字母:相同字母
x 所以,公因式是指数:最低次幂13 x原式=3x(x-2)例题精讲最大公因数为3= 3a的最低指数为1ab的最低指数为1b(3a–5bc)= – 4st2(3s2–2t+1)pq(5q+7p+3)1.注意:首项为负,
应提出负号。2.注意:
多项式中,
第三项是 -4st,
提系数后是1;
它在因式分解
时不能漏掉。提公因式法分解因式正确地找出多项式各项的公因式。注意:1、原多项式是几项,提公因式后也剩几项。
2、当多项式的某一项和公因式相同时,提公因式 后剩余的项是1。
3、当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号。
例2 把 9x2– 6xy+3xz 分解因式.=3x·3x - 3x·2y + 3x·z 解:=3x (3x-2y+z)9x2 – 6 x y + 3x z 例3(2)把 -24x3 –12x2 +28x 分解因式.当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号。
解:原式==小颖解的有误吗?
把 8 a 3 b2 –12ab 3 c + ab分解因式.解:8 a3b2 –12ab3c + ab
= ab·8a2b - ab·12b2 c +ab·1
= ab(8a2b - 12b2c) 当多项式的某一项和公因式相同时,提公因式后剩余的项是1。错误议一议1、请说出下列多项式的公因式:(1) ma + mb
(2) 4kx - 8ky
(3) 5y3+20y2(4) a2b-2ab2+ab
(5) 4x2-8ax+2x
(6) 3(a+b)2-6(a+b)3m4k5y2ab2x3(a+b)2深入理解2、请将下列多项式分解因式:(1) ma + mb
(2) 4kx - 8ky
(3) 5y3+20y2(4) a2b-2ab2+ab
(5) 4x2-8ax+2x
(6) 3(a+b)2-6(a+b)3m4k5y2ab2x3(a+b)2深入理解m(a+b)4k(x-2y)5y2(y+4)ab(a-2b+1)2x(2x-4a+1)3(a+b)2(1-2a-2b) 怎样知道提出的不是公因式?随堂练习C(1)2x2 + 3x3 + x = x(2x +3x2)(2)a2c - 6a3c = 3a2(c - 2ac)(3)-2s3 + 4s2 - 6s = - s(2s2 + 4s - 6)(4)a2b + 6ab2 - 8a = -2ab(2a-3b) - 8a4.下列的分解因式对吗?如不对,请指出原因:应为: 原式=x(2x +3x2+1)应为: 原式=-2s(s2-2s+3)应为: 原式= a (ab+6b2-8)应为: 原式=a2c(1 -2a)? 25x-5
? 3 x3 -3x2 –9x
? 8a 2c+ 2b c
? -4a 3b3 +6 a2 b-2ab
? a(x-y)+by-bx 5把下列各式分解因式:
=5(5x-1)=3x(x2-x-3)=2c(4a2+b)=-2ab(2a2b2-3a+1)= (x-y)(a-b) =a(x-y)+b(y-x)=a(x-y)-b(x-y)做一做1、习题4.2 1,2,3题小小数学家 已知x3+x2+x+1=0,求1+x+x2+x3+…+x2006的值。聪明的同学,你能得到这个计算结果吗?(课余探索) 2. 思考:
公因式可能是多项式吗?如果可能,那又当如何分解因式呢?举例并尝试。作业
请把下列多项式写成整式的乘积的形式:
(1) x2+x=______;
(2)x2 – 1= ________.x(x+1)(x+1)(x-1) 像上面我们把一个多项式化成几个整式的乘积的形式,这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.回顾
(3) a2- b2 =(a + b) (a-b) (a+b) (a-b)a2 - b2整式乘法因式分解因式分解和整式乘法是相反方向的变形:a2+2ab+b2(a+b)2因式分解整式乘法深入理解创设情景 学校打算把操场重新规划一下,分为绿化带、运动场、主席台三个部分,如下图,计算操场总面积。abcm方法一:S = m ( a + b + c )方法二:S = ma + mb + mcmm方法一:S = m ( a + b + c )方法二:S = ma + mb + mc 在式子ma + mb + mc中,m是这个多项式中每一个项都含有的相同因式,叫做 。公因式ma + mb + mc = m ( a + b + c )如果多项式的各项有公因式,可以把这个公因式提出来,将多项式写成公因式与另一个因式的乘积的形式。这种分解因式的方法叫做提公因式法。提公因式法:提公因式法的一般步骤 :1、确定公因式; 2、提取公因式。将原多项式式除以公因式,得到一个新多项式,归纳总结ma + mb + mc = m ( a + b + c )3、把新多项式与公因式相乘。议一议中各项的公因式是什么? ①多项式②你能尝试将多项式因式分解吗?③多项式 中各项的公因式是什么?
你认为怎样确定一个多项式的公因式?结论:(1)各项系数是整数,系数的最大公约数是公因式的系数;
(2)各项都含有的字母的最低次幂的积是公因式的字母部分;
(3)公因式的系数与公因式字母部分的积是这个多项式的公因式. 正确找出多项式各项公因式的关键是什么?1、定系数:公因式的系数是多项式各项系数 的最大公约数。 2、定字母:字母取多项式中各项都含有的相同字母。
3、定指数:指数取相同字母指数的最低次幂.
4、多项式各项的公因式可以是单项式,也 可以是多项式.例: 找 3 x 2 – 6 x 的公因式。系数:最大
公约数。3字母:相同字母
x 所以,公因式是指数:最低次幂13 x原式=3x(x-2)例题精讲最大公因数为3= 3a的最低指数为1ab的最低指数为1b(3a–5bc)= – 4st2(3s2–2t+1)pq(5q+7p+3)1.注意:首项为负,
应提出负号。2.注意:
多项式中,
第三项是 -4st,
提系数后是1;
它在因式分解
时不能漏掉。提公因式法分解因式正确地找出多项式各项的公因式。注意:1、原多项式是几项,提公因式后也剩几项。
2、当多项式的某一项和公因式相同时,提公因式 后剩余的项是1。
3、当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号。
例2 把 9x2– 6xy+3xz 分解因式.=3x·3x - 3x·2y + 3x·z 解:=3x (3x-2y+z)9x2 – 6 x y + 3x z 例3(2)把 -24x3 –12x2 +28x 分解因式.当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号。
解:原式==小颖解的有误吗?
把 8 a 3 b2 –12ab 3 c + ab分解因式.解:8 a3b2 –12ab3c + ab
= ab·8a2b - ab·12b2 c +ab·1
= ab(8a2b - 12b2c) 当多项式的某一项和公因式相同时,提公因式后剩余的项是1。错误议一议1、请说出下列多项式的公因式:(1) ma + mb
(2) 4kx - 8ky
(3) 5y3+20y2(4) a2b-2ab2+ab
(5) 4x2-8ax+2x
(6) 3(a+b)2-6(a+b)3m4k5y2ab2x3(a+b)2深入理解2、请将下列多项式分解因式:(1) ma + mb
(2) 4kx - 8ky
(3) 5y3+20y2(4) a2b-2ab2+ab
(5) 4x2-8ax+2x
(6) 3(a+b)2-6(a+b)3m4k5y2ab2x3(a+b)2深入理解m(a+b)4k(x-2y)5y2(y+4)ab(a-2b+1)2x(2x-4a+1)3(a+b)2(1-2a-2b) 怎样知道提出的不是公因式?随堂练习C(1)2x2 + 3x3 + x = x(2x +3x2)(2)a2c - 6a3c = 3a2(c - 2ac)(3)-2s3 + 4s2 - 6s = - s(2s2 + 4s - 6)(4)a2b + 6ab2 - 8a = -2ab(2a-3b) - 8a4.下列的分解因式对吗?如不对,请指出原因:应为: 原式=x(2x +3x2+1)应为: 原式=-2s(s2-2s+3)应为: 原式= a (ab+6b2-8)应为: 原式=a2c(1 -2a)? 25x-5
? 3 x3 -3x2 –9x
? 8a 2c+ 2b c
? -4a 3b3 +6 a2 b-2ab
? a(x-y)+by-bx 5把下列各式分解因式:
=5(5x-1)=3x(x2-x-3)=2c(4a2+b)=-2ab(2a2b2-3a+1)= (x-y)(a-b) =a(x-y)+b(y-x)=a(x-y)-b(x-y)做一做1、习题4.2 1,2,3题小小数学家 已知x3+x2+x+1=0,求1+x+x2+x3+…+x2006的值。聪明的同学,你能得到这个计算结果吗?(课余探索) 2. 思考:
公因式可能是多项式吗?如果可能,那又当如何分解因式呢?举例并尝试。作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
