人教版高中物理必修二第六章6.3 万有定律课件(共24张PPT)
文档属性
| 名称 | 人教版高中物理必修二第六章6.3 万有定律课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-01 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
6.3万有引力定律
复习:写出太阳与行星之间引力的表达式
一、牛顿的月、地印证:
1、问题提出:月亮绕地球做圆周运动的向心力、地面上物体的重力,都是地球对它们的吸引力,地球对月球的吸引力,地球对地面上物体的吸引力和太阳对行星的吸引力,是不是同种性质的引力?是否满足同样的规律?如何验证?
2、当时已知的数据:
地表重力加速度g = 9.8m/s2、地球半径R =6400km、月求公转周期T = 27.3天≈2.36×106s、月球轨道半径:r ≈ 60R。 请大家列出验证表达式:
验证式
G:叫为引力常量,
G=6.67259×10-11N·m2/kg2≈6.67×10-11N·m2/kg2
2、表达式:
二、万有引力定律
1、内容:
自然界中任何两个物体都是相互吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比。
r:为两物体的中心距离。通常把天体看做质量均匀分布的球体,r为两天体球心间的距离。
3、对万有引力定律的理解
⑴适用条件
①格地讲,万有引力只有适用于质点间的相互作用,即两物体间的距离远大于物体的大小。
②两个质量分布均匀的球体或球壳间的相互作用,也可用万有引力定律来计算,其中r是两个球体球心间的距离。
说明:①当两物体不能看作质点时,必须把物体分割成许多微小的物体,两物体间的引力为各微小物体间的引力的矢量和。
②当r→0时,两物体不能看做质点,故公式不适用。
⑵万有引力的相互性:两个物体相互作用的引力是一对作用力和反作用力,他们大小相等,方向相反,分别作用在两个物体上。
⑶万有引力的普适性:宇宙中任何有质量的物体之间的都存在相互吸的引力,它是自然界中物质之间的基本相互作用之一。
⑷引力的方向:在两物体中心的连线上。
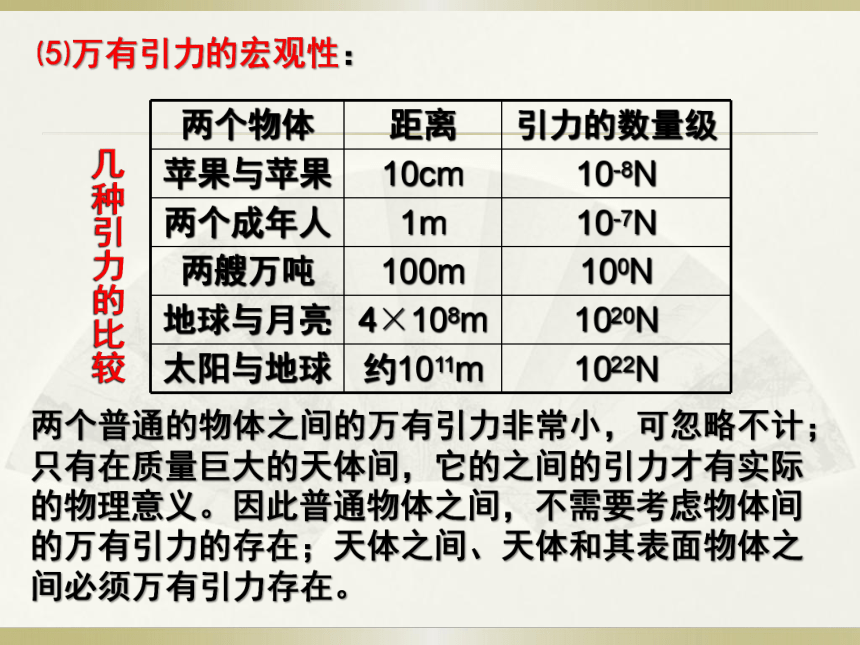
⑸万有引力的宏观性:
几种引力的比较
两个普通的物体之间的万有引力非常小,可忽略不计;只有在质量巨大的天体间,它的之间的引力才有实际的物理意义。因此普通物体之间,不需要考虑物体间的万有引力的存在;天体之间、天体和其表面物体之间必须万有引力存在。
两个物体 距离 引力的数量级
苹果与苹果 10cm 10-8N
两个成年人 1m 10-7N
两艘万吨 100m 100N
地球与月亮 4×108m 1020N
太阳与地球 约1011m 1022N
三、引力常量的测量——扭秤实验
物理学的许多重大发现是在该实验室做出的走,从这里走出20多名诺贝尔奖获得者。
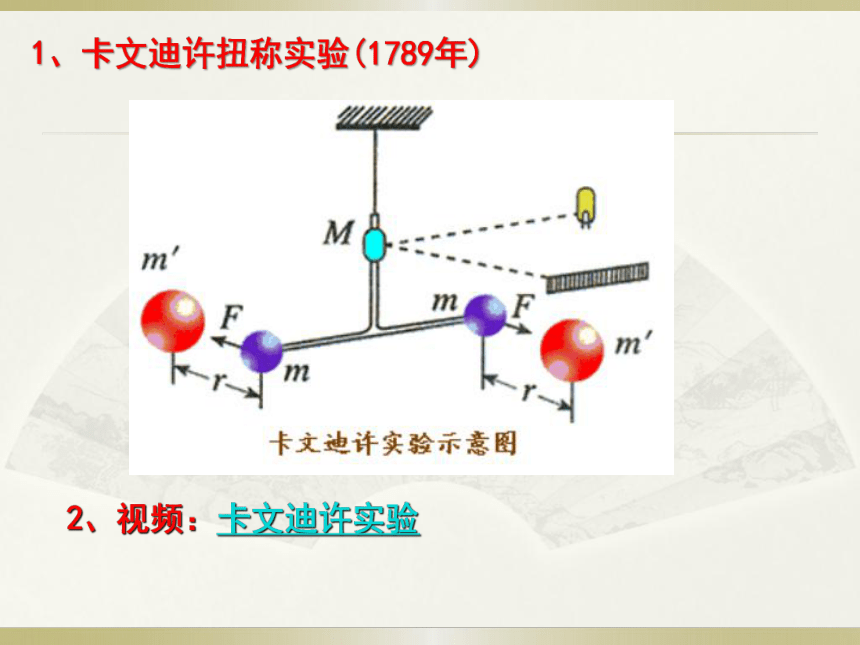
1、卡文迪许扭称实验(1789年)
2、视频:卡文迪许实验
3、卡文迪许扭称实验的意义
①证明了万有引力的存在,使万有引力定律进入了真正实用的时代。
②开创了微小量测量的先河,使科学放大思想得到推广。
③卡文迪许被称为“第一个称量地球质量的人”为什么?
④G值的物理含义:两个质量为1kg的物体相距1m时,它们之间万有引力为6.67×10-11 N
四、地球对物体引力与物体的重力的区别
1、地面附近的物体:
⑴重力与引力的关系
地球对地面上物体的吸引力产生两个作用效果:一、是提供物体随地球自转所需的向心力;二、是使物体对地面有压力作用(大小即为物体的重力)。故:除地球两极外,重力是引力的一个分力。
⑵重力与引力的方向:
引力指向地心,重力竖直向下;在两极和赤道,重力与引力都是指向地心的。
若地球看做均质的圆,引力方向与地球表面垂直,地球表面的切面不是水平面,重力方向跟地球表面的切面不垂直。如图所示
⑶重力与引力的大小:
①向心力随纬度的增加而减小;重力随纬度的增加而增大;向心力始终远小于重力;重力非常接近引力。在两极重力就是引力。且重力、引力都随高度的增大而减小。
②大小关系:mg ≤ F引
⑷地面上的物体受力分析问题:
①对不考虑地球自转,把地面看做静止不动的问题:对地面上的物体进行受力分析时,均认为物体受重力作用,不说物体受引力作用,且认为重力大小近似为引力大小。可通过万有引力定律来计算重力的大小。即: mg≈GMm/R2(R为地球半径)
②对考虑地球自转的问题:对地面上的物体进行受力分物体随地析时,则认为物体受引力作用,重力是引力的一个分力。物体在引力、支持力作用下随地球做匀速圆周运动。
③考虑地球自转时,引力与重力的关系:
在两极:F引=mg 在赤道:
注:只有在分析物体的重力、重力加速度随地理位置变化时,才考虑地球自转,其他情况地面都看做静止。
2、高空的卫星:
由于高空(高度与地球的半径相当)的物体,不受地球自转的影响。重力就是引力,引力就是重力。即:F引=mg
对卫星受力分析时,通常说物体受引力作用,一般不讲受重力作用。实际上,重力的概念是对地面上物体的引入的,对高空的卫星只有引力概念,重力只是引力的代名词。
五、例题:
例題1:⑴太空人乘坐火箭离开地球,当其体重减半时,火箭离地高度为地球半径之几倍?
⑵两个大小相同的实心小铁球紧靠在一起时,它们之间的万有引力为F。若半径为原来两倍的实心大铁球紧靠在一起时,则它们之间的万有引力为:( )
A、4F B、2F
C、F D、16F
D
例題2:某星球其平均密度与地球相同,半径为地球两倍,在地球上重量为 640N的人到该星球上时,其重量为:( )
A、160N B、320N
C、1280N D、2560N。
C
例题3:如图所示,阴影区域是质量为M、半径为R的均质球体挖去一个小球后剩余部分。所挖去的小球的半径为R/2,其球心0/与大球球心0间的距离为R/2。求大球剩余部分对位于0/0的延长线上,离球心0的距离为2R,质量为m的质点P的引力的大小。
例题4:在一个质量均匀分布,密度为ρ的无限大的空间内,有两个质量分别为M、m,半径分别为R、r的均质球体,两球体球心间的距离为d。求两球所受的万有引力各多大。
例题5:如图所示,在火箭的平台上放有一测试仪,火箭从地面启动后,以加速度:a=g/2竖直向上做匀加速运动(g为地球表面的重力加速度),当火箭上升到某一高度时,测试仪对平台的压力为启动前的17/18。地球的半径为R,求此时火箭离地面的高度。
解:设仪器的质量为m,对测试仪
在地面上:
在升降机上:
由题意有:
解上述4式得:
例题6:某行星的质量为M,半径为R。在该行星的表面,把一物体从行星的两极移到赤道时,物体的重力减小了1%。万有引力常量为G。求
⑴求该行星自转的周期。
⑵设该行星自转的角速度逐渐增大,则自转的角速度为多大时赤道上的物体将会飘起来。
例题7:理论和实际证明:放在均质球壳内任意一点的质点,球壳对质点万有引力为零。试利用此结论求:
⑴一个实心的均质球,质量为M,半径为R 。在均质球内,距球心r 处有一质量为m的质点。求质点所受的万有引力的大小(万有引力常量为G)。
⑵假定地球为均质的球体,地球表面的重力加速度为g,地球半径为R。求距地球表面h深处的重力加速度。
例题8:已知地球的半径为R,地球表面的重力加速度为g,地球的平均密度为ρ0。若地球内部某区域有一密度为ρ(ρ< ρ0),半径为r(rr)。由于该煤矿区的存在,会造成的该区域表面重力加速度的减小。求该区域重力加速度减小量的最大值。
6.3万有引力定律
复习:写出太阳与行星之间引力的表达式
一、牛顿的月、地印证:
1、问题提出:月亮绕地球做圆周运动的向心力、地面上物体的重力,都是地球对它们的吸引力,地球对月球的吸引力,地球对地面上物体的吸引力和太阳对行星的吸引力,是不是同种性质的引力?是否满足同样的规律?如何验证?
2、当时已知的数据:
地表重力加速度g = 9.8m/s2、地球半径R =6400km、月求公转周期T = 27.3天≈2.36×106s、月球轨道半径:r ≈ 60R。 请大家列出验证表达式:
验证式
G:叫为引力常量,
G=6.67259×10-11N·m2/kg2≈6.67×10-11N·m2/kg2
2、表达式:
二、万有引力定律
1、内容:
自然界中任何两个物体都是相互吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比。
r:为两物体的中心距离。通常把天体看做质量均匀分布的球体,r为两天体球心间的距离。
3、对万有引力定律的理解
⑴适用条件
①格地讲,万有引力只有适用于质点间的相互作用,即两物体间的距离远大于物体的大小。
②两个质量分布均匀的球体或球壳间的相互作用,也可用万有引力定律来计算,其中r是两个球体球心间的距离。
说明:①当两物体不能看作质点时,必须把物体分割成许多微小的物体,两物体间的引力为各微小物体间的引力的矢量和。
②当r→0时,两物体不能看做质点,故公式不适用。
⑵万有引力的相互性:两个物体相互作用的引力是一对作用力和反作用力,他们大小相等,方向相反,分别作用在两个物体上。
⑶万有引力的普适性:宇宙中任何有质量的物体之间的都存在相互吸的引力,它是自然界中物质之间的基本相互作用之一。
⑷引力的方向:在两物体中心的连线上。
⑸万有引力的宏观性:
几种引力的比较
两个普通的物体之间的万有引力非常小,可忽略不计;只有在质量巨大的天体间,它的之间的引力才有实际的物理意义。因此普通物体之间,不需要考虑物体间的万有引力的存在;天体之间、天体和其表面物体之间必须万有引力存在。
两个物体 距离 引力的数量级
苹果与苹果 10cm 10-8N
两个成年人 1m 10-7N
两艘万吨 100m 100N
地球与月亮 4×108m 1020N
太阳与地球 约1011m 1022N
三、引力常量的测量——扭秤实验
物理学的许多重大发现是在该实验室做出的走,从这里走出20多名诺贝尔奖获得者。
1、卡文迪许扭称实验(1789年)
2、视频:卡文迪许实验
3、卡文迪许扭称实验的意义
①证明了万有引力的存在,使万有引力定律进入了真正实用的时代。
②开创了微小量测量的先河,使科学放大思想得到推广。
③卡文迪许被称为“第一个称量地球质量的人”为什么?
④G值的物理含义:两个质量为1kg的物体相距1m时,它们之间万有引力为6.67×10-11 N
四、地球对物体引力与物体的重力的区别
1、地面附近的物体:
⑴重力与引力的关系
地球对地面上物体的吸引力产生两个作用效果:一、是提供物体随地球自转所需的向心力;二、是使物体对地面有压力作用(大小即为物体的重力)。故:除地球两极外,重力是引力的一个分力。
⑵重力与引力的方向:
引力指向地心,重力竖直向下;在两极和赤道,重力与引力都是指向地心的。
若地球看做均质的圆,引力方向与地球表面垂直,地球表面的切面不是水平面,重力方向跟地球表面的切面不垂直。如图所示
⑶重力与引力的大小:
①向心力随纬度的增加而减小;重力随纬度的增加而增大;向心力始终远小于重力;重力非常接近引力。在两极重力就是引力。且重力、引力都随高度的增大而减小。
②大小关系:mg ≤ F引
⑷地面上的物体受力分析问题:
①对不考虑地球自转,把地面看做静止不动的问题:对地面上的物体进行受力分析时,均认为物体受重力作用,不说物体受引力作用,且认为重力大小近似为引力大小。可通过万有引力定律来计算重力的大小。即: mg≈GMm/R2(R为地球半径)
②对考虑地球自转的问题:对地面上的物体进行受力分物体随地析时,则认为物体受引力作用,重力是引力的一个分力。物体在引力、支持力作用下随地球做匀速圆周运动。
③考虑地球自转时,引力与重力的关系:
在两极:F引=mg 在赤道:
注:只有在分析物体的重力、重力加速度随地理位置变化时,才考虑地球自转,其他情况地面都看做静止。
2、高空的卫星:
由于高空(高度与地球的半径相当)的物体,不受地球自转的影响。重力就是引力,引力就是重力。即:F引=mg
对卫星受力分析时,通常说物体受引力作用,一般不讲受重力作用。实际上,重力的概念是对地面上物体的引入的,对高空的卫星只有引力概念,重力只是引力的代名词。
五、例题:
例題1:⑴太空人乘坐火箭离开地球,当其体重减半时,火箭离地高度为地球半径之几倍?
⑵两个大小相同的实心小铁球紧靠在一起时,它们之间的万有引力为F。若半径为原来两倍的实心大铁球紧靠在一起时,则它们之间的万有引力为:( )
A、4F B、2F
C、F D、16F
D
例題2:某星球其平均密度与地球相同,半径为地球两倍,在地球上重量为 640N的人到该星球上时,其重量为:( )
A、160N B、320N
C、1280N D、2560N。
C
例题3:如图所示,阴影区域是质量为M、半径为R的均质球体挖去一个小球后剩余部分。所挖去的小球的半径为R/2,其球心0/与大球球心0间的距离为R/2。求大球剩余部分对位于0/0的延长线上,离球心0的距离为2R,质量为m的质点P的引力的大小。
例题4:在一个质量均匀分布,密度为ρ的无限大的空间内,有两个质量分别为M、m,半径分别为R、r的均质球体,两球体球心间的距离为d。求两球所受的万有引力各多大。
例题5:如图所示,在火箭的平台上放有一测试仪,火箭从地面启动后,以加速度:a=g/2竖直向上做匀加速运动(g为地球表面的重力加速度),当火箭上升到某一高度时,测试仪对平台的压力为启动前的17/18。地球的半径为R,求此时火箭离地面的高度。
解:设仪器的质量为m,对测试仪
在地面上:
在升降机上:
由题意有:
解上述4式得:
例题6:某行星的质量为M,半径为R。在该行星的表面,把一物体从行星的两极移到赤道时,物体的重力减小了1%。万有引力常量为G。求
⑴求该行星自转的周期。
⑵设该行星自转的角速度逐渐增大,则自转的角速度为多大时赤道上的物体将会飘起来。
例题7:理论和实际证明:放在均质球壳内任意一点的质点,球壳对质点万有引力为零。试利用此结论求:
⑴一个实心的均质球,质量为M,半径为R 。在均质球内,距球心r 处有一质量为m的质点。求质点所受的万有引力的大小(万有引力常量为G)。
⑵假定地球为均质的球体,地球表面的重力加速度为g,地球半径为R。求距地球表面h深处的重力加速度。
例题8:已知地球的半径为R,地球表面的重力加速度为g,地球的平均密度为ρ0。若地球内部某区域有一密度为ρ(ρ< ρ0),半径为r(r
