人教版数学八年级下册 18.1 平行四边形 同步练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册 18.1 平行四边形 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 126.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-01 00:00:00 | ||
图片预览

文档简介
平行四边形 同步练习
一.选择题(共12小题)
1.下列结论正确的是( )
A.平行四边形是轴对称图形
B.平行四边形的对角线相等
C.平行四边形的对边平行且相等
D.平行四边形的对角互补,邻角相等
2.平行四边形的边长为5,则它的对角线长可能是( )
A.4和6 B.2和12 C.4和8 D.4和3
3.平面直角坐标系中一个平行四边形的三个顶点的坐标分别(0,0),(3,0),(1,3),则第四个顶点的坐标可能是下列坐标:①(4,3)②(-2,3)③(-1,-3)④(2,-3)中的哪几个( )
A.①②③ B.②③④ C.①②④ D.①③④
4.如图,在?ABCD中,∠B=60°,AB=4,对角线AC⊥AB,则?ABCD的面积为( )
A.6
B.12
C.12
D.16
5.如图,在△ABC中,D是AC边的中点,且BD⊥AC,ED∥BC,ED交AB于点E,若AC=4,BC=6,则△ADE的周长为( )
A.6 B.8 C.10 D.12
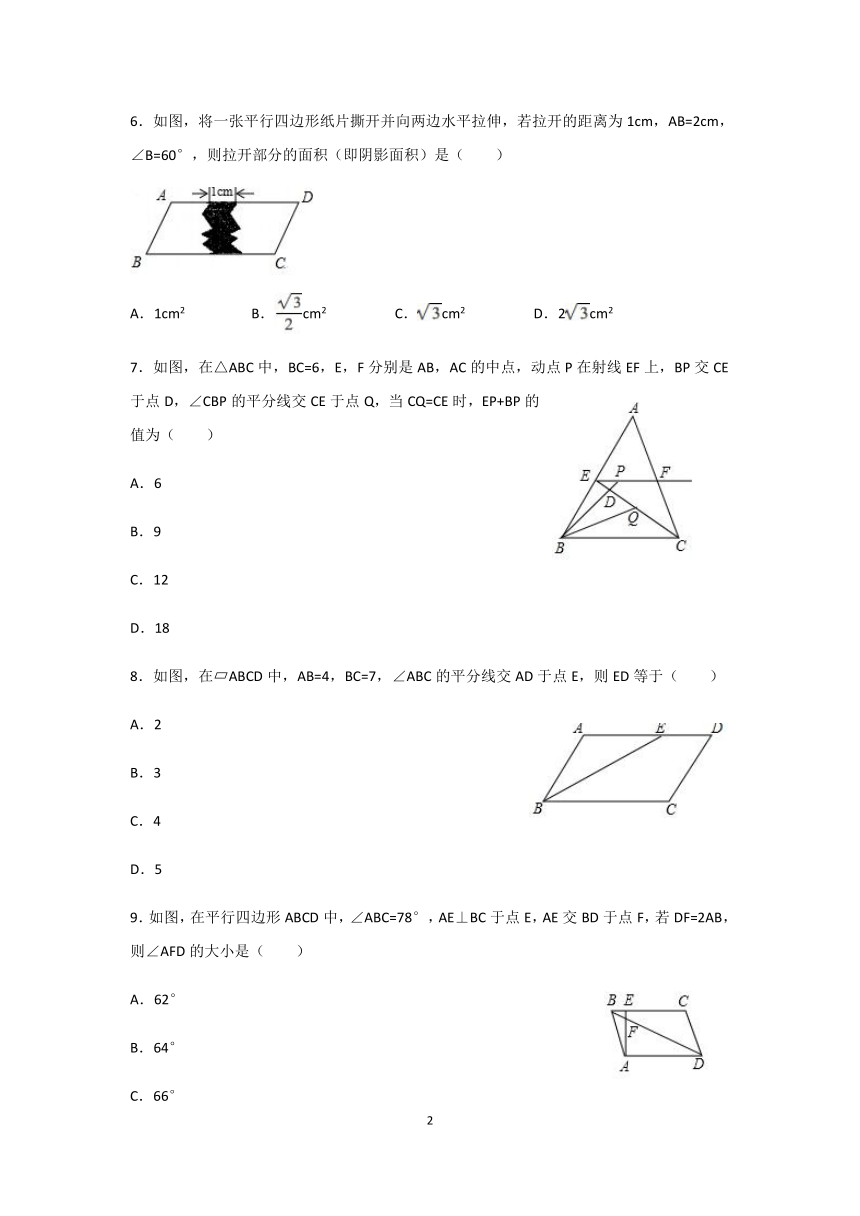
6.如图,将一张平行四边形纸片撕开并向两边水平拉伸,若拉开的距离为1cm,AB=2cm,∠B=60°,则拉开部分的面积(即阴影面积)是( )
A.1cm2 B.cm2 C.cm2 D.2cm2
7.如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=CE时,EP+BP的值为( )
A.6
B.9
C.12
D.18
8.如图,在?ABCD中,AB=4,BC=7,∠ABC的平分线交AD于点E,则ED等于( )
A.2
B.3
C.4
D.5
9.如图,在平行四边形ABCD中,∠ABC=78°,AE⊥BC于点E,AE交BD于点F,若DF=2AB,则∠AFD的大小是( )
A.62°
B.64°
C.66°
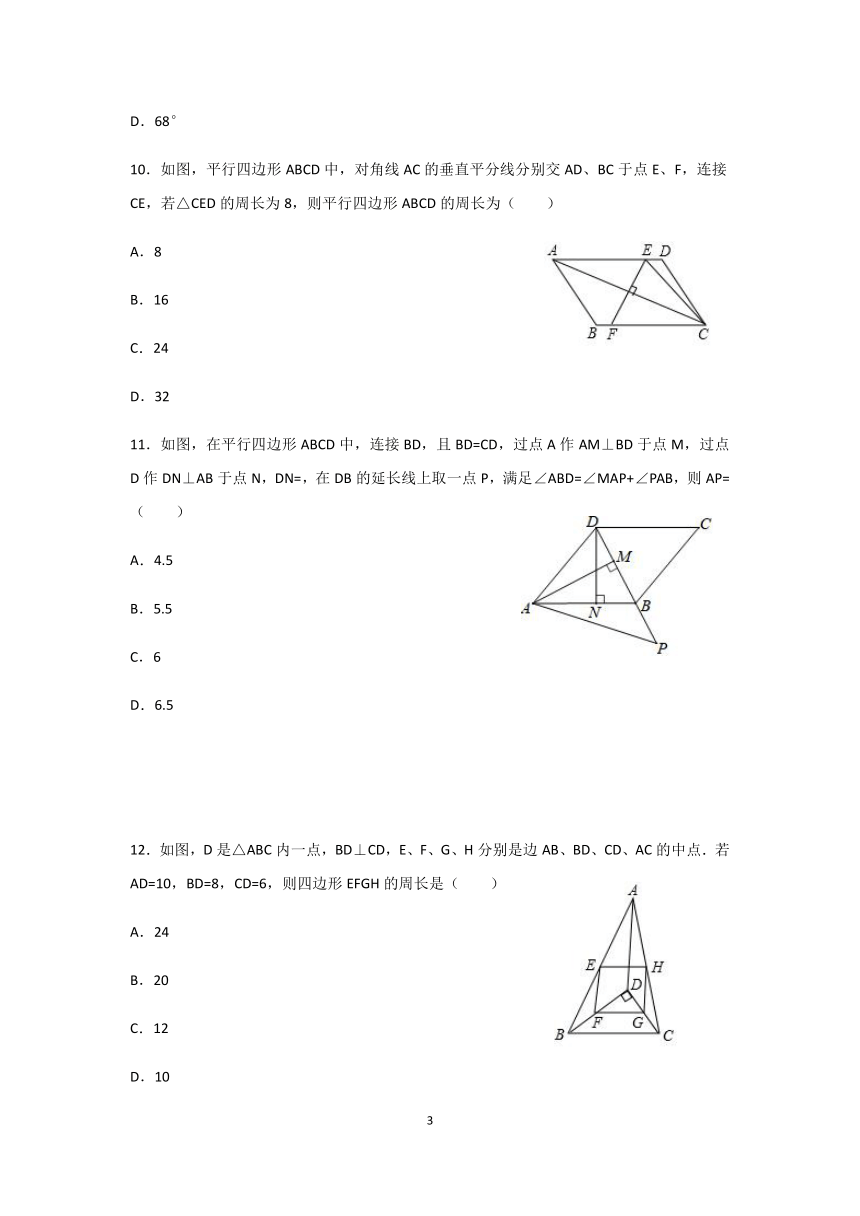
D.68°
10.如图,平行四边形ABCD中,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,若△CED的周长为8,则平行四边形ABCD的周长为( )
A.8
B.16
C.24
D.32
11.如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,DN=,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=( )
A.4.5
B.5.5
C.6
D.6.5
12.如图,D是△ABC内一点,BD⊥CD,E、F、G、H分别是边AB、BD、CD、AC的中点.若AD=10,BD=8,CD=6,则四边形EFGH的周长是( )
A.24
B.20
C.12
D.10
二.填空题(共6小题)
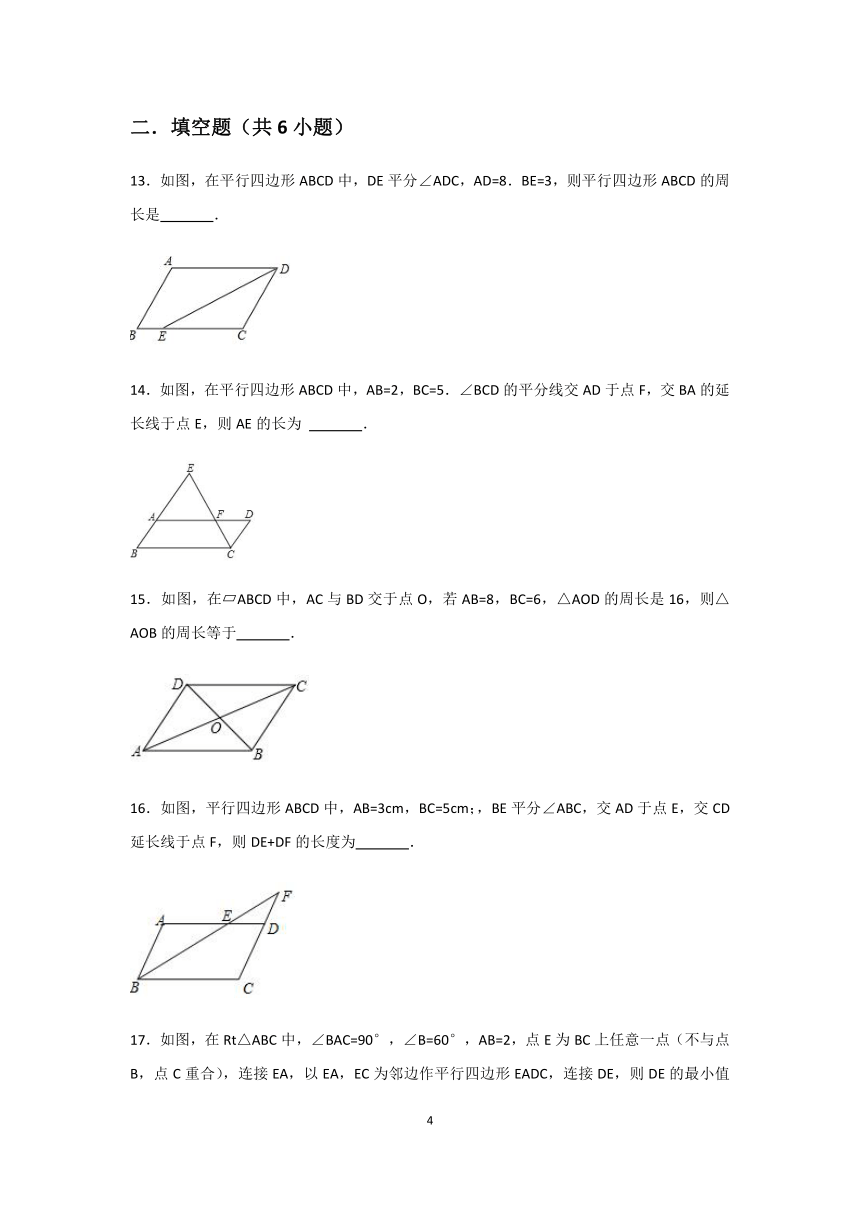
13.如图,在平行四边形ABCD中,DE平分∠ADC,AD=8.BE=3,则平行四边形ABCD的周长是 .
14.如图,在平行四边形ABCD中,AB=2,BC=5.∠BCD的平分线交AD于点F,交BA的延长线于点E,则AE的长为 .
15.如图,在?ABCD中,AC与BD交于点O,若AB=8,BC=6,△AOD的周长是16,则△AOB的周长等于 .
16.如图,平行四边形ABCD中,AB=3cm,BC=5cm;,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为 .
17.如图,在Rt△ABC中,∠BAC=90°,∠B=60°,AB=2,点E为BC上任意一点(不与点B,点C重合),连接EA,以EA,EC为邻边作平行四边形EADC,连接DE,则DE的最小值为 .
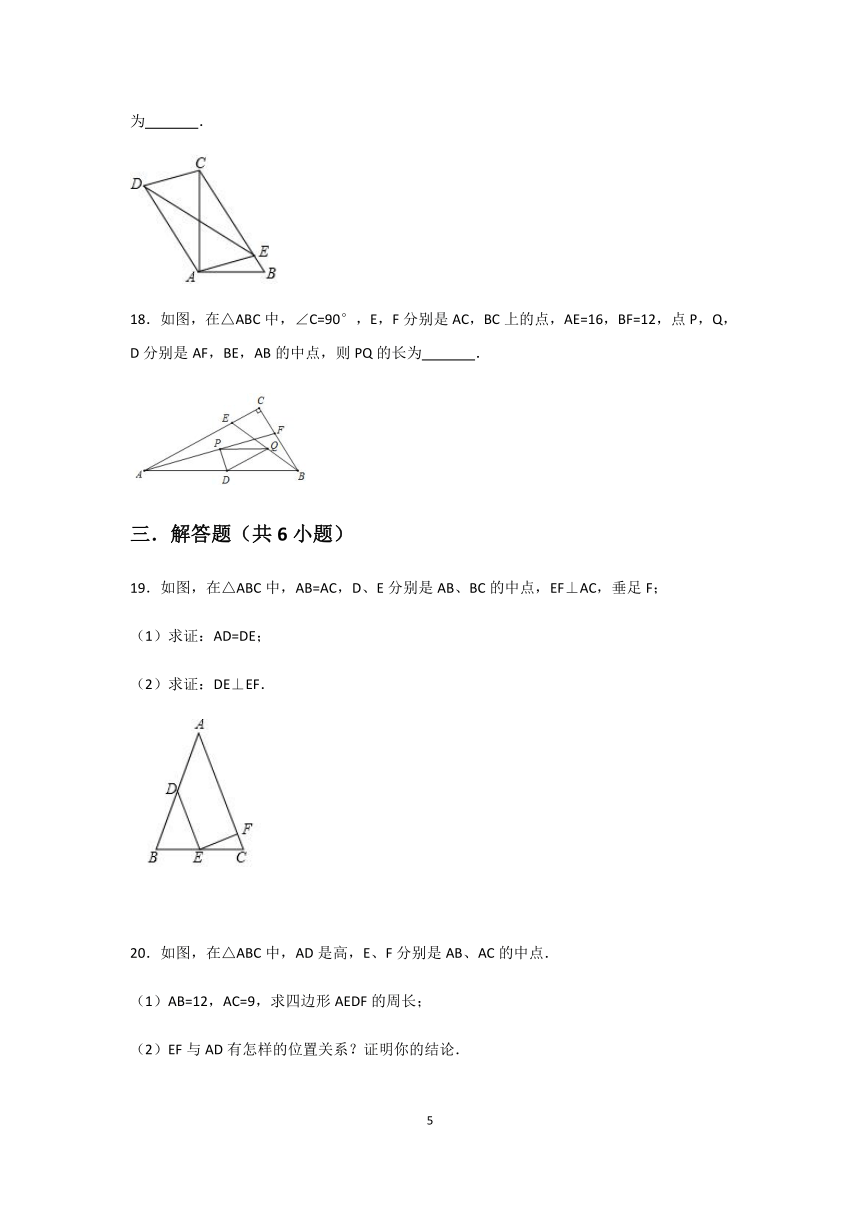
18.如图,在△ABC中,∠C=90°,E,F分别是AC,BC上的点,AE=16,BF=12,点P,Q,D分别是AF,BE,AB的中点,则PQ的长为 .
三.解答题(共6小题)
19.如图,在△ABC中,AB=AC,D、E分别是AB、BC的中点,EF⊥AC,垂足F;
(1)求证:AD=DE;
(2)求证:DE⊥EF.
20.如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)AB=12,AC=9,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系?证明你的结论.
21.如图所示平行四边形ABCD中,EF分别是边AD,BC上的点,且AE=CF.
(1)求证:BE=DF;
(2)连结AF,若AD=DF,∠ADF=40°,求∠AFB的度数.
22.如图所示,在△ABC中,点D在BC上且CD=CA,CF平分∠ACB,AE=EB,求证:EF=BD.
23.已知,如图,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
24.如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠E=∠F,AD=BC.
(1)求证:O是线段AC的中点:
(2)连接AF、EC,证明四边形AFCE是平行四边形.
参考答案
1-5:CCCDB 6-10:CCBBB 11-12:CB
13、26
14、3
15、18
16、4
10
19、:(1)∵AB=AC,
∴∠B=∠C,
∵D、E分别是AB、BC的中点,
∴AD=AB,DE=AC,
∴AD=DE;
(2)∵D、E分别是AB、BC的中点,
∴DE∥AC,
∵EF⊥AC,
∴DE⊥EF.
20、:(1)∵AD是高,
∴∠ADB=∠ADC=90°,
∵E、F分别是AB、AC的中点,
∴ED=EB=AB,DF=FC=AC,
∵AB=12,AC=9,
∴AE+ED=12,AF+DF=9,
∴四边形AEDF的周长为12+9=21;
(2)EF⊥AD,
理由:∵DE=AE,DF=AF,
∴点E、F在线段AD的垂直平分线上,
∴EF⊥AD.
21、(1)证明:在平行四边形ABCD中,AD∥BC,AD=BC,
∵AE=CF,
∴DE∥BF,DE=BF
∴四边形BEDF是平行四边形
∴BE=DF.
(2)∵AD=DF,∠ADF=40°
∴∠DAF=∠AFD=70°
∵AD∥BC
∴∠AFB=∠FAD=70°.
22、证明:∵CD=CA,CF平分∠ACB,
∴F是AD中点,
∵AE=EB,
∴E是AB中点,∴EF是△ABD的中位线,
∴EF=BD
23、:(1)四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∴∠EAM=∠FCN,
又∵AD∥BC,
∴∠E=∠F.
∵在△AEM与△CFN中,
∴△AEM≌△CFN(ASA);
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD
又由(1)得AM=CN,
∴BM=DN,BM∥DN,
∴四边形BMDN是平行四边形.
24、证明:(1)∵∠E=∠F,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴AC,BD互相平分;
即O是线段AC的中点.
(2)∵AD∥BC,
∴∠EAC=∠FCA,
在△OAE和△OCF中,
∴△OAE≌△OCF(ASA).
∴OE=OF,
∴四边形AFCE是平行四边形
一.选择题(共12小题)
1.下列结论正确的是( )
A.平行四边形是轴对称图形
B.平行四边形的对角线相等
C.平行四边形的对边平行且相等
D.平行四边形的对角互补,邻角相等
2.平行四边形的边长为5,则它的对角线长可能是( )
A.4和6 B.2和12 C.4和8 D.4和3
3.平面直角坐标系中一个平行四边形的三个顶点的坐标分别(0,0),(3,0),(1,3),则第四个顶点的坐标可能是下列坐标:①(4,3)②(-2,3)③(-1,-3)④(2,-3)中的哪几个( )
A.①②③ B.②③④ C.①②④ D.①③④
4.如图,在?ABCD中,∠B=60°,AB=4,对角线AC⊥AB,则?ABCD的面积为( )
A.6
B.12
C.12
D.16
5.如图,在△ABC中,D是AC边的中点,且BD⊥AC,ED∥BC,ED交AB于点E,若AC=4,BC=6,则△ADE的周长为( )
A.6 B.8 C.10 D.12
6.如图,将一张平行四边形纸片撕开并向两边水平拉伸,若拉开的距离为1cm,AB=2cm,∠B=60°,则拉开部分的面积(即阴影面积)是( )
A.1cm2 B.cm2 C.cm2 D.2cm2
7.如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=CE时,EP+BP的值为( )
A.6
B.9
C.12
D.18
8.如图,在?ABCD中,AB=4,BC=7,∠ABC的平分线交AD于点E,则ED等于( )
A.2
B.3
C.4
D.5
9.如图,在平行四边形ABCD中,∠ABC=78°,AE⊥BC于点E,AE交BD于点F,若DF=2AB,则∠AFD的大小是( )
A.62°
B.64°
C.66°
D.68°
10.如图,平行四边形ABCD中,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,若△CED的周长为8,则平行四边形ABCD的周长为( )
A.8
B.16
C.24
D.32
11.如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,DN=,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=( )
A.4.5
B.5.5
C.6
D.6.5
12.如图,D是△ABC内一点,BD⊥CD,E、F、G、H分别是边AB、BD、CD、AC的中点.若AD=10,BD=8,CD=6,则四边形EFGH的周长是( )
A.24
B.20
C.12
D.10
二.填空题(共6小题)
13.如图,在平行四边形ABCD中,DE平分∠ADC,AD=8.BE=3,则平行四边形ABCD的周长是 .
14.如图,在平行四边形ABCD中,AB=2,BC=5.∠BCD的平分线交AD于点F,交BA的延长线于点E,则AE的长为 .
15.如图,在?ABCD中,AC与BD交于点O,若AB=8,BC=6,△AOD的周长是16,则△AOB的周长等于 .
16.如图,平行四边形ABCD中,AB=3cm,BC=5cm;,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为 .
17.如图,在Rt△ABC中,∠BAC=90°,∠B=60°,AB=2,点E为BC上任意一点(不与点B,点C重合),连接EA,以EA,EC为邻边作平行四边形EADC,连接DE,则DE的最小值为 .
18.如图,在△ABC中,∠C=90°,E,F分别是AC,BC上的点,AE=16,BF=12,点P,Q,D分别是AF,BE,AB的中点,则PQ的长为 .
三.解答题(共6小题)
19.如图,在△ABC中,AB=AC,D、E分别是AB、BC的中点,EF⊥AC,垂足F;
(1)求证:AD=DE;
(2)求证:DE⊥EF.
20.如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)AB=12,AC=9,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系?证明你的结论.
21.如图所示平行四边形ABCD中,EF分别是边AD,BC上的点,且AE=CF.
(1)求证:BE=DF;
(2)连结AF,若AD=DF,∠ADF=40°,求∠AFB的度数.
22.如图所示,在△ABC中,点D在BC上且CD=CA,CF平分∠ACB,AE=EB,求证:EF=BD.
23.已知,如图,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
24.如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠E=∠F,AD=BC.
(1)求证:O是线段AC的中点:
(2)连接AF、EC,证明四边形AFCE是平行四边形.
参考答案
1-5:CCCDB 6-10:CCBBB 11-12:CB
13、26
14、3
15、18
16、4
10
19、:(1)∵AB=AC,
∴∠B=∠C,
∵D、E分别是AB、BC的中点,
∴AD=AB,DE=AC,
∴AD=DE;
(2)∵D、E分别是AB、BC的中点,
∴DE∥AC,
∵EF⊥AC,
∴DE⊥EF.
20、:(1)∵AD是高,
∴∠ADB=∠ADC=90°,
∵E、F分别是AB、AC的中点,
∴ED=EB=AB,DF=FC=AC,
∵AB=12,AC=9,
∴AE+ED=12,AF+DF=9,
∴四边形AEDF的周长为12+9=21;
(2)EF⊥AD,
理由:∵DE=AE,DF=AF,
∴点E、F在线段AD的垂直平分线上,
∴EF⊥AD.
21、(1)证明:在平行四边形ABCD中,AD∥BC,AD=BC,
∵AE=CF,
∴DE∥BF,DE=BF
∴四边形BEDF是平行四边形
∴BE=DF.
(2)∵AD=DF,∠ADF=40°
∴∠DAF=∠AFD=70°
∵AD∥BC
∴∠AFB=∠FAD=70°.
22、证明:∵CD=CA,CF平分∠ACB,
∴F是AD中点,
∵AE=EB,
∴E是AB中点,∴EF是△ABD的中位线,
∴EF=BD
23、:(1)四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∴∠EAM=∠FCN,
又∵AD∥BC,
∴∠E=∠F.
∵在△AEM与△CFN中,
∴△AEM≌△CFN(ASA);
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD
又由(1)得AM=CN,
∴BM=DN,BM∥DN,
∴四边形BMDN是平行四边形.
24、证明:(1)∵∠E=∠F,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴AC,BD互相平分;
即O是线段AC的中点.
(2)∵AD∥BC,
∴∠EAC=∠FCA,
在△OAE和△OCF中,
∴△OAE≌△OCF(ASA).
∴OE=OF,
∴四边形AFCE是平行四边形
