高中数学人教A版必修5第2章第1节《数列的概念与简单表示法》课件(共29张PPT)
文档属性
| 名称 | 高中数学人教A版必修5第2章第1节《数列的概念与简单表示法》课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 312.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-02 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
2.1 数列的概念与
简单表示法
(1)人们在1740年发现了一颗彗星,并推算出这颗彗星每隔83年出现一次,那么从发现那次算起,这颗彗星出现的年份依次为
(2)四名同学在5次考试中的成绩:
甲:60,70,80,90,100
乙:80,80,80,80,80
丙:100,90,80,70,60
丁:90,100,90,100,90
1、考察下面的问题
1740,1823,1960,1989,2072,…
问题创设
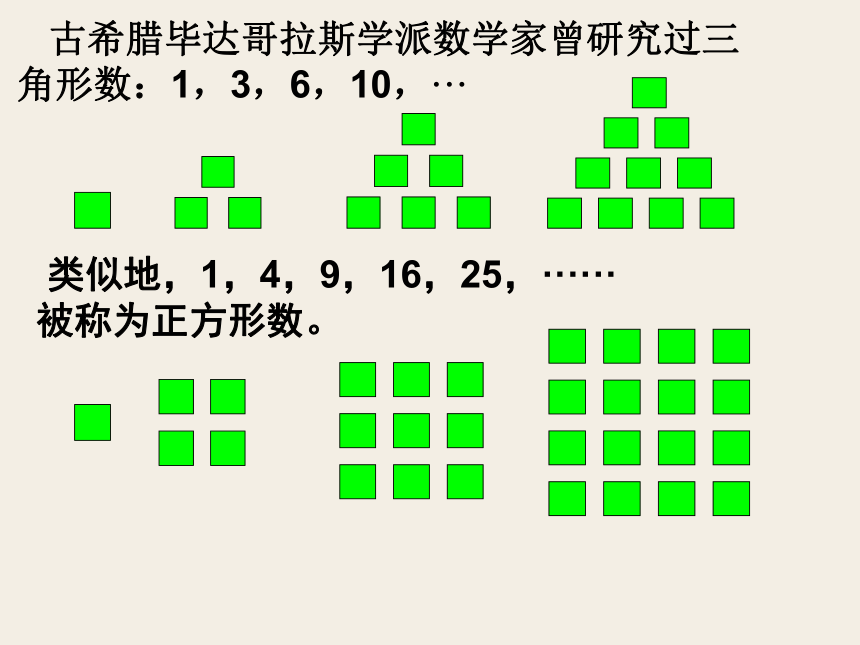
古希腊毕达哥拉斯学派数学家曾研究过三角形数:1,3,6,10,···
类似地,1,4,9,16,25,······
被称为正方形数。
一、数列的概念:
按照一定顺序排列着的一列数称为数列
注意:(1)数列有顺序,但不一定要有规律.
(2)数列中的项是确定的,且可以重复。
(3){an}表示一个数列:a1,a2,a3,…,an,….
an表示数列{an}中的第n项
数列中的每一个数叫做这个数列的项
各项依次叫做这个数列的第1项(或首项),
第2项,…,第n项.
数列的一般形式写成
a1,a2,a3,…,an,…. (n∈N*)
简记作{an} 。读作:数列an
知识巩固1.下列数列的关系是 ( )
①1,4,9,16,25;
②25,16,9,4,1;
③9,4,1,16,25;
A.都是同一个数列 B.都不相同
C.①②是同一个数列 D.②③是同一个数列
B
1740,1823,1960,1989,2072,…
1,3,6,10,···
1,4,9,16,25,······
四名同学在5次考试中的成绩:
甲:60,70,80,90,100
乙:80,80,80,80,80
丙:100,90,80,70,60
丁:90,100,90,100,90
二、数列的分类:
1、按项数来分类:
(1)有穷数列:
(2)无穷数列:
项数有限的数列
项数无限的数列
2、按各项的大小关系(单调性)来分类:
甲:60,70,80,90,100
丙:100,90,80,70,60
二、数列的分类:
(1)递增数列:
从第2项起,每一项都大于它的前一项
的数列 ;
记作:an+1>an
从第2项起,每一项都小于它的前一项
的数列 ;
记作:an+1(2)递减数列:
(3)常 数 列:
(4)摆动数列:
各项都相等的数列
从第2项起,有些项大于它的前一项,
有些项小于它的前一项的数列
2、按各项的大小关系(单调性)来分类:
丁:90,100,90,100,90
二、数列的分类:
乙:80,80,80,80,80
三、数列的表示方法:
(1)列举法:
a1,a2,a3,…,an,…. 简记作{an}
(2)列表法:
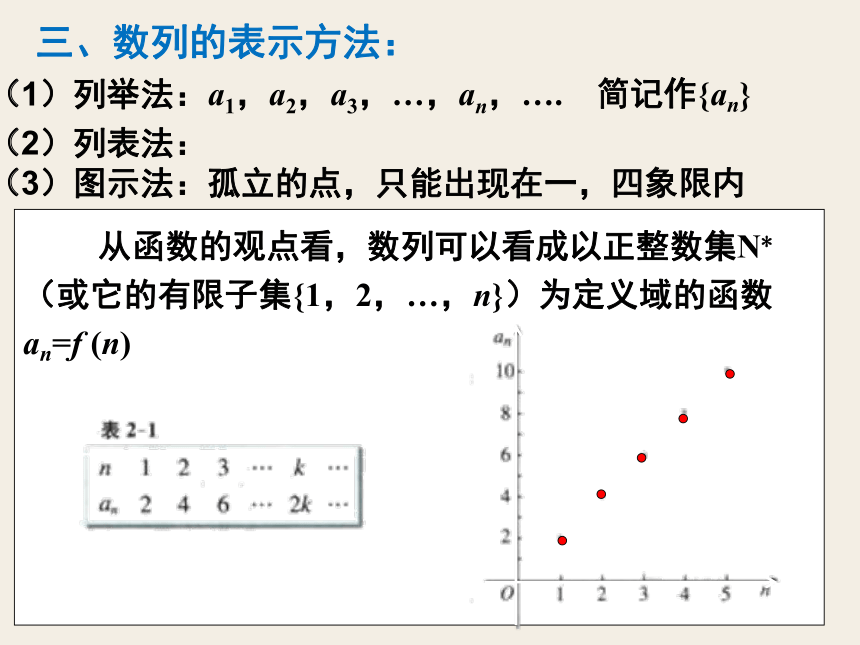
(3)图示法:孤立的点,只能出现在一,四象限内
从函数的观点看,数列可以看成以正整数集N*
(或它的有限子集{1,2,…,n})为定义域的函数
an=f (n)
如:数列2,4,6,8,......
an=2n (n∈N*)
(4)通项公式法:
三、数列的表示方法:
数列的第n项an与序号n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式,简称通项
题型一:通项公式
知识巩固3.试写出下面数列的一个通项公式,使它的
前4项分别是下列各数:
(1)1,3,5,7....... (2)1,2,4,8......
(3)1,4,9,16....... (4)2,6,12,20,30.......
(5)9,99,999,9999,...... (6)3,33,333,3333,......
题型一:通项公式
知识巩固3.试写出下面数列的一个通项公式,使它的
前4项分别是下列各数:
题型一:通项公式
知识巩固3.试写出下面数列的一个通项公式,使它的
前4项分别是下列各数:
(9)-1,1,-1,1,..... (10)1,-2,3,-4,...
(11)2,0,2,0,.......
注意:①通项公式的主要作用是“知序号可求项”
如:数列{n2}的第11项是_______
②一些数列的通项公式不是唯一的;
③不是每一个数列都能写出它的通项公式。
如:1,24,8,3,19
121
题型一:通项公式
学生练习:数列1,3,6,10,.....的一个通项公式为( )
C
(5)递推公式法:数列的项与项之间的关系可以用一个式子来表示,这个式子叫做这个数列的递推公式。
三、数列的表示方法:
1,3,5,7,9,......
题型二:递推公式
知识巩固4.写出下面数列{an}的前5项:
题型二:递推公式
知识巩固5
题型三:数列的单调性
知识巩固6.判断并证明以下数列的单调性
题型三:数列的单调性
知识巩固6.判断并证明以下数列的单调性
总结:
判断并证明数列单调性的方法:
(1)作差法;
(2)作商法(各项为正数时);
(3)利用对应函数的单调性;
四、数列的前n项和:
一般地,我们称 为数列{an} 的前n项和 ,用 Sn 表示,
即
拓展:数列的前n项积:
一般地,我们称 为数列{an} 的前n项和 ,用 Tn 表示,
即
题型四:数列的前n项和
知识巩固7.
变式:
课堂总结:
通项公式
数列的概念
表示方法
分类
列表
图象
项数
有穷数列
无穷数列
递增
数列
递减
数列
摆动
数列
常
数列
大小
函数
数列
本课结束
2.1 数列的概念与
简单表示法
(1)人们在1740年发现了一颗彗星,并推算出这颗彗星每隔83年出现一次,那么从发现那次算起,这颗彗星出现的年份依次为
(2)四名同学在5次考试中的成绩:
甲:60,70,80,90,100
乙:80,80,80,80,80
丙:100,90,80,70,60
丁:90,100,90,100,90
1、考察下面的问题
1740,1823,1960,1989,2072,…
问题创设
古希腊毕达哥拉斯学派数学家曾研究过三角形数:1,3,6,10,···
类似地,1,4,9,16,25,······
被称为正方形数。
一、数列的概念:
按照一定顺序排列着的一列数称为数列
注意:(1)数列有顺序,但不一定要有规律.
(2)数列中的项是确定的,且可以重复。
(3){an}表示一个数列:a1,a2,a3,…,an,….
an表示数列{an}中的第n项
数列中的每一个数叫做这个数列的项
各项依次叫做这个数列的第1项(或首项),
第2项,…,第n项.
数列的一般形式写成
a1,a2,a3,…,an,…. (n∈N*)
简记作{an} 。读作:数列an
知识巩固1.下列数列的关系是 ( )
①1,4,9,16,25;
②25,16,9,4,1;
③9,4,1,16,25;
A.都是同一个数列 B.都不相同
C.①②是同一个数列 D.②③是同一个数列
B
1740,1823,1960,1989,2072,…
1,3,6,10,···
1,4,9,16,25,······
四名同学在5次考试中的成绩:
甲:60,70,80,90,100
乙:80,80,80,80,80
丙:100,90,80,70,60
丁:90,100,90,100,90
二、数列的分类:
1、按项数来分类:
(1)有穷数列:
(2)无穷数列:
项数有限的数列
项数无限的数列
2、按各项的大小关系(单调性)来分类:
甲:60,70,80,90,100
丙:100,90,80,70,60
二、数列的分类:
(1)递增数列:
从第2项起,每一项都大于它的前一项
的数列 ;
记作:an+1>an
从第2项起,每一项都小于它的前一项
的数列 ;
记作:an+1
(3)常 数 列:
(4)摆动数列:
各项都相等的数列
从第2项起,有些项大于它的前一项,
有些项小于它的前一项的数列
2、按各项的大小关系(单调性)来分类:
丁:90,100,90,100,90
二、数列的分类:
乙:80,80,80,80,80
三、数列的表示方法:
(1)列举法:
a1,a2,a3,…,an,…. 简记作{an}
(2)列表法:
(3)图示法:孤立的点,只能出现在一,四象限内
从函数的观点看,数列可以看成以正整数集N*
(或它的有限子集{1,2,…,n})为定义域的函数
an=f (n)
如:数列2,4,6,8,......
an=2n (n∈N*)
(4)通项公式法:
三、数列的表示方法:
数列的第n项an与序号n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式,简称通项
题型一:通项公式
知识巩固3.试写出下面数列的一个通项公式,使它的
前4项分别是下列各数:
(1)1,3,5,7....... (2)1,2,4,8......
(3)1,4,9,16....... (4)2,6,12,20,30.......
(5)9,99,999,9999,...... (6)3,33,333,3333,......
题型一:通项公式
知识巩固3.试写出下面数列的一个通项公式,使它的
前4项分别是下列各数:
题型一:通项公式
知识巩固3.试写出下面数列的一个通项公式,使它的
前4项分别是下列各数:
(9)-1,1,-1,1,..... (10)1,-2,3,-4,...
(11)2,0,2,0,.......
注意:①通项公式的主要作用是“知序号可求项”
如:数列{n2}的第11项是_______
②一些数列的通项公式不是唯一的;
③不是每一个数列都能写出它的通项公式。
如:1,24,8,3,19
121
题型一:通项公式
学生练习:数列1,3,6,10,.....的一个通项公式为( )
C
(5)递推公式法:数列的项与项之间的关系可以用一个式子来表示,这个式子叫做这个数列的递推公式。
三、数列的表示方法:
1,3,5,7,9,......
题型二:递推公式
知识巩固4.写出下面数列{an}的前5项:
题型二:递推公式
知识巩固5
题型三:数列的单调性
知识巩固6.判断并证明以下数列的单调性
题型三:数列的单调性
知识巩固6.判断并证明以下数列的单调性
总结:
判断并证明数列单调性的方法:
(1)作差法;
(2)作商法(各项为正数时);
(3)利用对应函数的单调性;
四、数列的前n项和:
一般地,我们称 为数列{an} 的前n项和 ,用 Sn 表示,
即
拓展:数列的前n项积:
一般地,我们称 为数列{an} 的前n项和 ,用 Tn 表示,
即
题型四:数列的前n项和
知识巩固7.
变式:
课堂总结:
通项公式
数列的概念
表示方法
分类
列表
图象
项数
有穷数列
无穷数列
递增
数列
递减
数列
摆动
数列
常
数列
大小
函数
数列
本课结束
