第18章 勾股定理复习课课件 (共24张PPT)
文档属性
| 名称 | 第18章 勾股定理复习课课件 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-02 09:03:01 | ||
图片预览







文档简介
(共24张PPT)
第18章 勾股定理复习课
沪科版 八年级下
新知导入
问题1.请叙述勾股定理的内容?
勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
问题2.请叙述勾股定理逆定理的内容?
勾股定理的逆定理:如果三角形的三边长a 、b 、c 满足 a2+b2=c2
那么这个三角形是直角三角形.
问题3.你知道几组勾股数?
(3,4,5)(6,8,10)(5,12,13)(8,15,17)(9,12,15)等等.
新知讲解
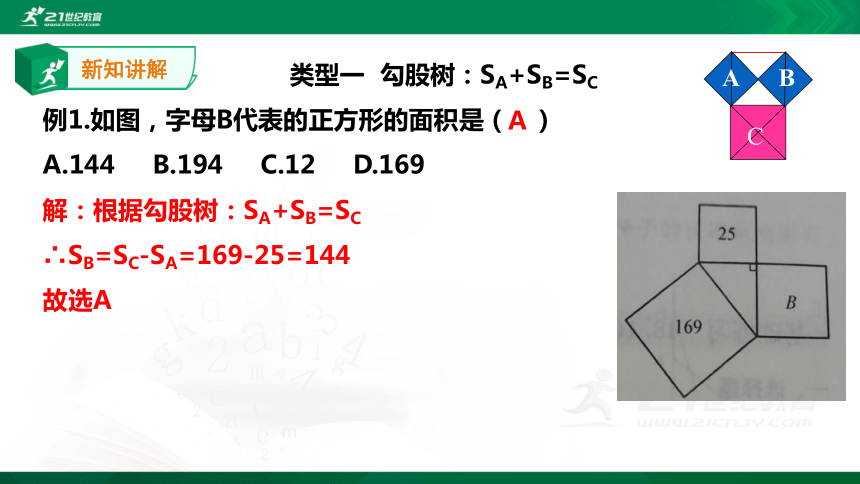
类型一 勾股树:SA+SB=SC
例1.如图,字母B代表的正方形的面积是( )
A.144 B.194 C.12 D.169
解:根据勾股树:SA+SB=SC
∴SB=SC-SA=169-25=144
故选A
A
新知讲解
变式练习1.如图,以Rt△ABC三边为直径分别向形外作半圆,S1,S2,S3分别是这三个半圆的面积,若S1=10,S2=8,则S3=( )
A. B.2 C. D.6
解:根据勾股树:SA+SB=SC
∴S3=S1-S2=10-8=2
故选B
B
新知讲解
类型二 梯子问题(关键点:梯子的长度不变)
例2.一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
(3)当梯子的顶端下滑的距离与梯子的底端在水平方向滑动的距离相等时,这时这个梯子的顶端距地面有多高?
新知讲解
解:(1)在Rt△AOB中,根据勾股定理:
AO2=AB2-OB2=252-72=576,
又∵AO>0,∴AO=24.
答:这个梯子的顶端距地面24米.
(2)在Rt△A'OB'中,根据勾股定理:
B'O2=A'B'2-A'O2=252-202=225,
又∵B'O>0,∴B'O=15.∴BB'=OB'-OB=15-7=8米
答:梯子的底端在水平方向滑动了8米.
新知讲解
(3)设AA'=BB'=x米
在Rt△A‘OB’中,根据勾股定理:
A‘B'2=OA'2+OB'2=(24-x)2+(7+x)2=252,
∴x1=17,x2=0(舍去)
∴OA'=OA-AA'=24-17=7米
答:这时梯子的顶端距地面7米.
新知讲解
变式练习1.如图,长为5米的梯子靠在墙上,梯子的底端A到墙根O的距离为2米,现将梯子的底端A向外移动1米到A',同时梯子的顶端B下降至B',那么BB'的长度应①等于1米;②大于1米;③小于1米.其中正确的结论的序号是———.
③
新知讲解
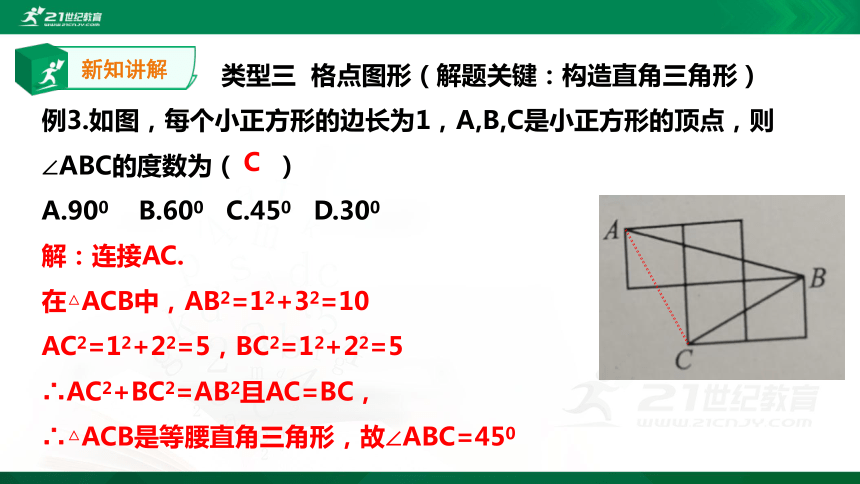
类型三 格点图形(解题关键:构造直角三角形)
例3.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则
∠ABC的度数为( )
A.900 B.600 C.450 D.300
解:连接AC.
在△ACB中,AB2=12+32=10
AC2=12+22=5,BC2=12+22=5
∴AC2+BC2=AB2且AC=BC,
∴△ACB是等腰直角三角形,故∠ABC=450
C
新知讲解
变式练习1.如图,每个小正方形的边长为1,则图中的
四边形的周长是( )
变式练习2.如图,每个小正方形的边长为1,求BC边
上的高.
解:连接AO,并延长AO交BC于M点。
根据题意得:AB=AC=
又OB=OC,
故AM垂直平分BC
O
M
新知讲解
由勾股定理得: BC=
∴BM=
在Rt△ABM中,根据勾股定理:
AM2=AB2-BM2=( )2-( )2= ,
∴AM=
新知讲解
类型四 立体图形的展开图
例4.有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B 处,问梯子最短需多少米(已知油罐的底面半径是2 m,高AB 是5 m,π取3)?
B
A
B
A
B'
A'
新知讲解
解:油罐的展开图如图,则AB'为梯子的最短距离.
∵AA'=2×3×2=12, A'B'=5,
∴AB'=13. 即梯子最短需13米.
数学思想:
立体图形
转化
展开
平面图形
新知讲解
【变式题】看到小蚂蚁终于喝到饮料的兴奋劲儿,小明又灵光乍现,拿出了牛奶盒,把小蚂蚁放在了点A处,并在点B 处放上了点儿火腿肠粒,你能帮小蚂蚁找到完成任务的最短路程么?
牛奶盒
A
B
10cm
6cm
8cm
新知讲解
A
B
B1
B2
B3
解:由题意知有三种展开方法,如图.由勾股定理得
AB12 =102 +(6+8)2 =296,
AB22= 82 +(10+6)2 =320,
AB32= 62 +(10+8)2 =360,
∴AB1<AB2<AB3.
∴小蚂蚁完成任务的最短路程为AB1,长为 .
课堂练习
1.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D面积分别为9,25, 1, 9,则最大正方形E的边长是( )
A.12 B.44
C. D.无法确定
C
课堂练习
2.如图,每个小正方形的边长为1,?ABC的三边a,b,c的大小关系式
为( )
A. aC. c
C
拓展提高
3.如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
解:在Rt△ABC中,根据勾股定理得
OB2=AB2-OA2=2.62-2.42=1,∴OB=1.
在Rt△COD中,根据勾股定理得
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,
∴梯子的顶端沿墙下滑0.5m时,
梯子底端并不是也外移0.5m,而是外移约0.77m.
中考链接
4.(无锡中考)如图,是一个边长为1的正方体硬纸盒,现在A处有一只蚂蚁,想沿着正方体的外表面到达B 处吃食物,求蚂蚁爬行的最短距离是多少.
解:由题意得AC =2,BC=1,
在Rt△ABC 中,由勾股定理得 :AB ?= AC ?+ BC ?=2?+1?=5
∴AB= ,即最短路程为 .
A
B
转化成平面图形
课堂总结
本节课你有什么收获?
本节课我们主要学习了勾股定理四种类型的应用:
类型一 勾股树:SA+SB=SC
类型二 梯子问题(关键点:梯子的长度不变)
类型三 格点图形(解题关键:构造直角三角形)
类型四 立体图形的展开图
板书设计
第18章 勾股定理的复习课
1.类型一 勾股树:SA+SB=SC
2.类型二 梯子问题(关键点:梯子的长度不变)
3.类型三 格点图形(解题关键:构造直角三角形)
4.类型四 立体图形的展开图
作业布置
课 本 P65 页
习 题 5--8 题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第18章 勾股定理复习课
沪科版 八年级下
新知导入
问题1.请叙述勾股定理的内容?
勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
问题2.请叙述勾股定理逆定理的内容?
勾股定理的逆定理:如果三角形的三边长a 、b 、c 满足 a2+b2=c2
那么这个三角形是直角三角形.
问题3.你知道几组勾股数?
(3,4,5)(6,8,10)(5,12,13)(8,15,17)(9,12,15)等等.
新知讲解
类型一 勾股树:SA+SB=SC
例1.如图,字母B代表的正方形的面积是( )
A.144 B.194 C.12 D.169
解:根据勾股树:SA+SB=SC
∴SB=SC-SA=169-25=144
故选A
A
新知讲解
变式练习1.如图,以Rt△ABC三边为直径分别向形外作半圆,S1,S2,S3分别是这三个半圆的面积,若S1=10,S2=8,则S3=( )
A. B.2 C. D.6
解:根据勾股树:SA+SB=SC
∴S3=S1-S2=10-8=2
故选B
B
新知讲解
类型二 梯子问题(关键点:梯子的长度不变)
例2.一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
(3)当梯子的顶端下滑的距离与梯子的底端在水平方向滑动的距离相等时,这时这个梯子的顶端距地面有多高?
新知讲解
解:(1)在Rt△AOB中,根据勾股定理:
AO2=AB2-OB2=252-72=576,
又∵AO>0,∴AO=24.
答:这个梯子的顶端距地面24米.
(2)在Rt△A'OB'中,根据勾股定理:
B'O2=A'B'2-A'O2=252-202=225,
又∵B'O>0,∴B'O=15.∴BB'=OB'-OB=15-7=8米
答:梯子的底端在水平方向滑动了8米.
新知讲解
(3)设AA'=BB'=x米
在Rt△A‘OB’中,根据勾股定理:
A‘B'2=OA'2+OB'2=(24-x)2+(7+x)2=252,
∴x1=17,x2=0(舍去)
∴OA'=OA-AA'=24-17=7米
答:这时梯子的顶端距地面7米.
新知讲解
变式练习1.如图,长为5米的梯子靠在墙上,梯子的底端A到墙根O的距离为2米,现将梯子的底端A向外移动1米到A',同时梯子的顶端B下降至B',那么BB'的长度应①等于1米;②大于1米;③小于1米.其中正确的结论的序号是———.
③
新知讲解
类型三 格点图形(解题关键:构造直角三角形)
例3.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则
∠ABC的度数为( )
A.900 B.600 C.450 D.300
解:连接AC.
在△ACB中,AB2=12+32=10
AC2=12+22=5,BC2=12+22=5
∴AC2+BC2=AB2且AC=BC,
∴△ACB是等腰直角三角形,故∠ABC=450
C
新知讲解
变式练习1.如图,每个小正方形的边长为1,则图中的
四边形的周长是( )
变式练习2.如图,每个小正方形的边长为1,求BC边
上的高.
解:连接AO,并延长AO交BC于M点。
根据题意得:AB=AC=
又OB=OC,
故AM垂直平分BC
O
M
新知讲解
由勾股定理得: BC=
∴BM=
在Rt△ABM中,根据勾股定理:
AM2=AB2-BM2=( )2-( )2= ,
∴AM=
新知讲解
类型四 立体图形的展开图
例4.有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B 处,问梯子最短需多少米(已知油罐的底面半径是2 m,高AB 是5 m,π取3)?
B
A
B
A
B'
A'
新知讲解
解:油罐的展开图如图,则AB'为梯子的最短距离.
∵AA'=2×3×2=12, A'B'=5,
∴AB'=13. 即梯子最短需13米.
数学思想:
立体图形
转化
展开
平面图形
新知讲解
【变式题】看到小蚂蚁终于喝到饮料的兴奋劲儿,小明又灵光乍现,拿出了牛奶盒,把小蚂蚁放在了点A处,并在点B 处放上了点儿火腿肠粒,你能帮小蚂蚁找到完成任务的最短路程么?
牛奶盒
A
B
10cm
6cm
8cm
新知讲解
A
B
B1
B2
B3
解:由题意知有三种展开方法,如图.由勾股定理得
AB12 =102 +(6+8)2 =296,
AB22= 82 +(10+6)2 =320,
AB32= 62 +(10+8)2 =360,
∴AB1<AB2<AB3.
∴小蚂蚁完成任务的最短路程为AB1,长为 .
课堂练习
1.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D面积分别为9,25, 1, 9,则最大正方形E的边长是( )
A.12 B.44
C. D.无法确定
C
课堂练习
2.如图,每个小正方形的边长为1,?ABC的三边a,b,c的大小关系式
为( )
A. a
C
拓展提高
3.如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
解:在Rt△ABC中,根据勾股定理得
OB2=AB2-OA2=2.62-2.42=1,∴OB=1.
在Rt△COD中,根据勾股定理得
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,
∴梯子的顶端沿墙下滑0.5m时,
梯子底端并不是也外移0.5m,而是外移约0.77m.
中考链接
4.(无锡中考)如图,是一个边长为1的正方体硬纸盒,现在A处有一只蚂蚁,想沿着正方体的外表面到达B 处吃食物,求蚂蚁爬行的最短距离是多少.
解:由题意得AC =2,BC=1,
在Rt△ABC 中,由勾股定理得 :AB ?= AC ?+ BC ?=2?+1?=5
∴AB= ,即最短路程为 .
A
B
转化成平面图形
课堂总结
本节课你有什么收获?
本节课我们主要学习了勾股定理四种类型的应用:
类型一 勾股树:SA+SB=SC
类型二 梯子问题(关键点:梯子的长度不变)
类型三 格点图形(解题关键:构造直角三角形)
类型四 立体图形的展开图
板书设计
第18章 勾股定理的复习课
1.类型一 勾股树:SA+SB=SC
2.类型二 梯子问题(关键点:梯子的长度不变)
3.类型三 格点图形(解题关键:构造直角三角形)
4.类型四 立体图形的展开图
作业布置
课 本 P65 页
习 题 5--8 题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
