18.1.1平行四边形的性质
图片预览






文档简介
(共30张PPT)
华师大版 初中数学
18.1 平行四边形的性质
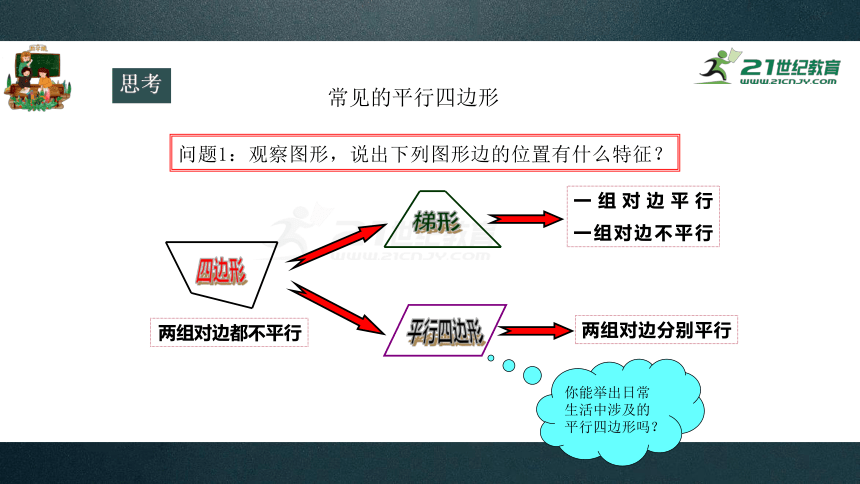
问题1:观察图形,说出下列图形边的位置有什么特征?
两组对边都不平行
一组对边平行
一组对边不平行
四边形
梯形
平行四边形
两组对边分别平行
你能举出日常生活中涉及的平行四边形吗?
思考
常见的平行四边形
生活中的平行四边形
新知导入
例如
平行四边形的定义:两组对边分别平行的四边形是平行四边形。
A
D
C
B
如图:四边形ABCD是平行四边形
记作:□ABCD
读作:平行四边形ABCD
温馨提示
(1)平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线;
(2)平行四边形相对的边称为对边;相对的角称为对角;
(3)平行四边形是特殊的四边形,特殊在两组对边分别平行哟!
平行四边形
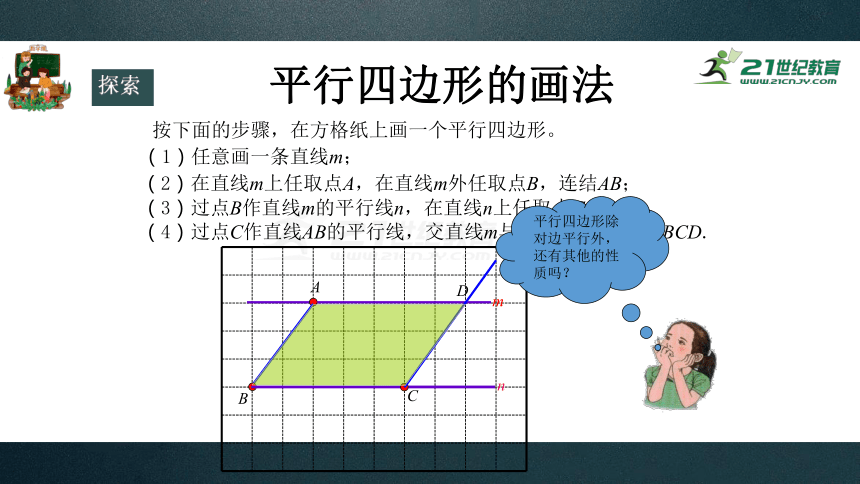
按下面的步骤,在方格纸上画一个平行四边形。
m
A
B
C
D
n
(1)任意画一条直线m;
(2)在直线m上任取点A,在直线m外任取点B,连结AB;
(3)过点B作直线m的平行线n,在直线n上任取点C;
(4)过点C作直线AB的平行线,交直线m与点D,就得到□ABCD.
平行四边形除对边平行外,还有其他的性质吗?
平行四边形的画法
探索
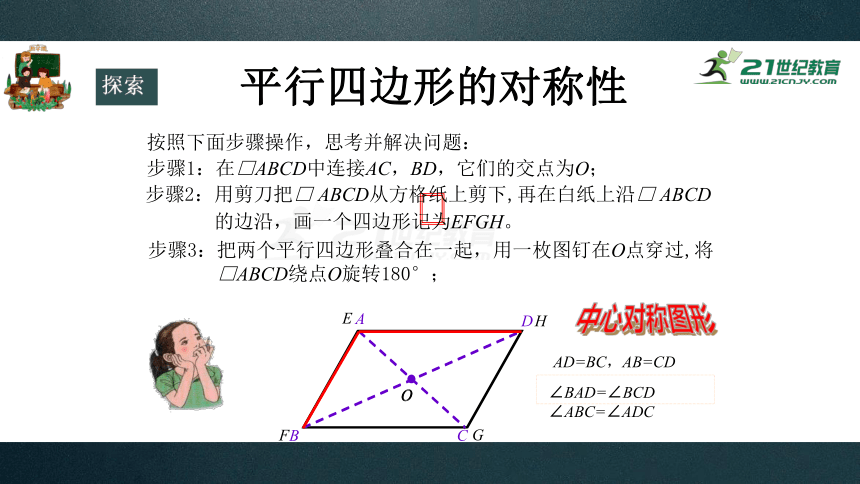
按照下面步骤操作,思考并解决问题:
步骤1:在□ABCD中连接AC,BD,它们的交点为O;
步骤3:把两个平行四边形叠合在一起,用一枚图钉在O点穿过,将
□ABCD绕点O旋转180°;
步骤2:用剪刀把□ ABCD从方格纸上剪下,再在白纸上沿□ ABCD
的边沿,画一个四边形记为EFGH。
A
B
C
D
O
E
H
G
F
O
中心对称图形
AD=BC,AB=CD
∠BAD=∠BCD
∠ABC=∠ADC
平行四边形的对称性
探索
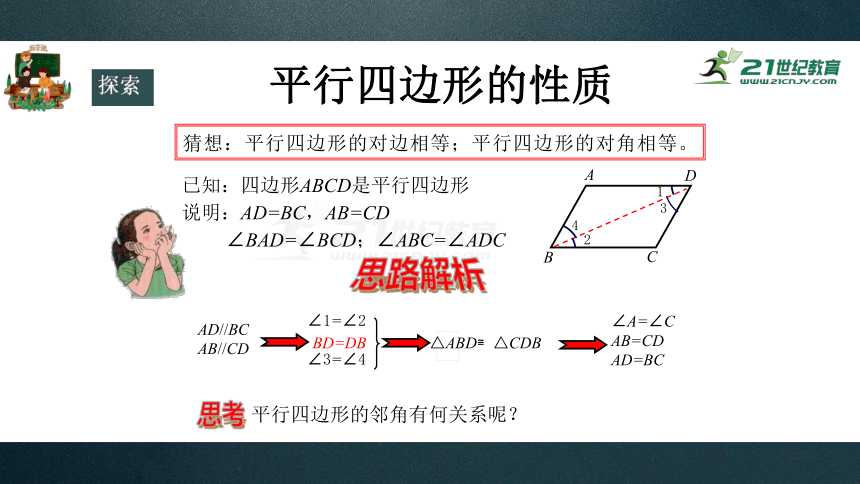
猜想:平行四边形的对边相等;平行四边形的对角相等。
A
B
C
D
已知:四边形ABCD是平行四边形
说明:AD=BC,AB=CD
∠BAD=∠BCD;∠ABC=∠ADC
1
2
3
4
BD=DB
∠1=∠2
∠3=∠4
思路解析
AD//BC
AB//CD
△ABD≌△CDB
∠A=∠C
AB=CD
AD=BC
思考
平行四边形的邻角有何关系呢?
平行四边形的性质
探索
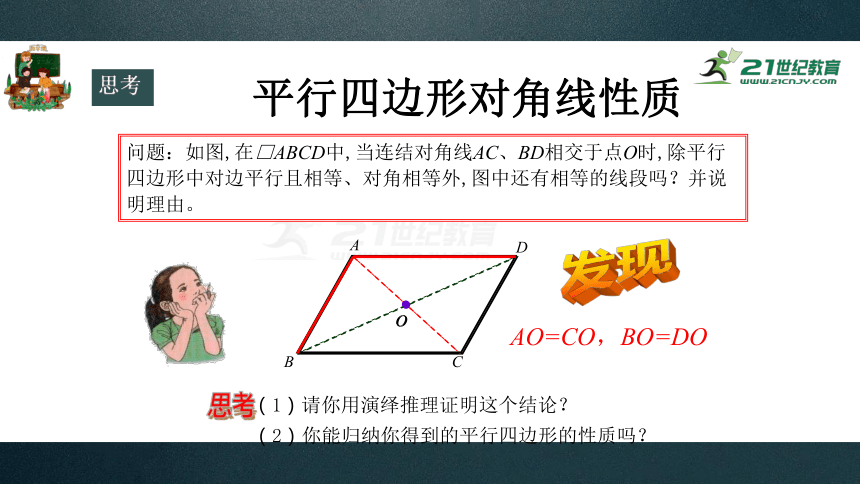
问题:如图,在□ABCD中,当连结对角线AC、BD相交于点O时,除平行四边形中对边平行且相等、对角相等外,图中还有相等的线段吗?并说明理由。
A
B
C
D
O
O
发现
AO=CO,BO=DO
思考
(1)请你用演绎推理证明这个结论?
(2)你能归纳你得到的平行四边形的性质吗?
平行四边形对角线性质
思考
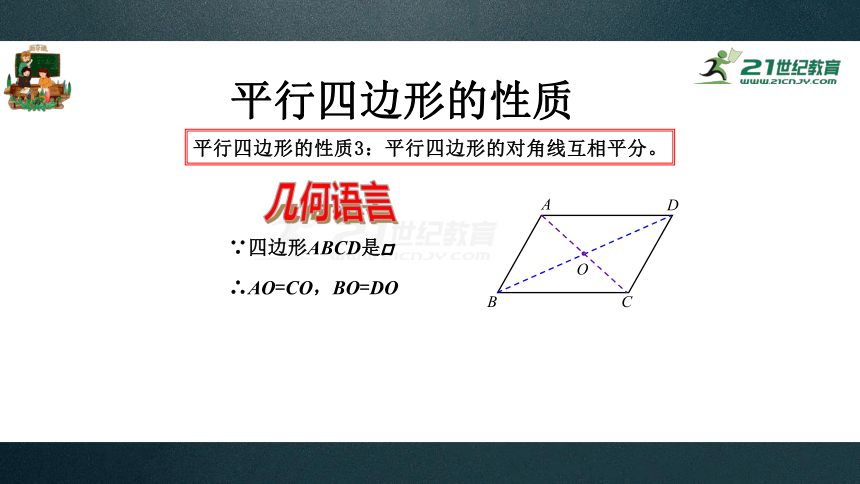
平行四边形的性质3:平行四边形的对角线互相平分。
A
B
C
D
O
几何语言
∴AO=CO,BO=DO
∵四边形ABCD是□
平行四边形的性质
例1 在□ABCD中,∠A=40 °,求其他各内角的大小.
解:在□ABCD中, ∠A=∠C,∠B=∠D(平行四边形的对角相等).
∵ ∠A=40°(已知),
∴ ∠C=40°.
又∵AD∥BC(平行四边形的对边平行),
∴∠A+∠B=180°(两直线平行,同旁内角互补).
∴∠B= 180 -∠A= 180?- 40°=140 °,
∠D= ∠B= 140 °.
新知讲解
例2 如图,在□ABCD中,AB=8,周长等于24.求其余三条边的长.
解: 在□ ABCD中,
AB=DC,AD=BC(平行四边形的对边相等).
∵AB=8,
∴DC=8,
又∵AB+BC+DC+AD=24,
∴ AD=BC= .
新知讲解
在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出平行线之间这些垂线段的长度.你能发现什么结论?试用平行四边形的性质定理加以说明.
两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离.
平行线之间的距离处处相等.
新知讲解
例3 已知平行四边形的周长是24,相邻两边的长度相差4,求该平行四边形相邻两边的长.
解:设AB的长为x,则BC的长为x+4.
根据已知,可得,
2(AB + BC)=24,即2(x +x +4)=24
4 x +8 =24,
解得x=4 .
所以,该平行四边形相邻两边的长分别为4和8 .
新知讲解
例4 已知:如图,在□ABCD中,∠ADC的平分线与AB相交于点E.求证:BE+BC=CD.
证明:∵四边形ABCD是平行四边形,
∴AB=CD(平行四边形的对边相等),
AB∥CD(平行四边形的对边平行),
∴∠CDE=∠AED.
又∵DE是∠ADC的平分线,
∴∠ADE=∠CDE, ∠ADE=∠AED,
∴AD=AE.
又∵AD=BC (平行四边形的对边相等),
∴ AE=BC.
BE+BC= BE+AE= CD.
新知讲解
例5 如图□ ABCD的对角线AC和 BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC与BD的和是多少?
解:在□ ABCD中
∵∴AB=6,AO+BO+AB=15,
∴AO+BO=15-6=9.
又∵AO=OC,BO=OD(平行四边形对角线互相平分),
∴AC+BD=2AO+2BO=2(AO+BO)=9×2=18.
新知讲解
例6 如图□ ABCD的对角线AC和BD相交于点O,EF过点O且与AB,CD相交于点E和点F.求证:OE=OF.
解:∵ABCD是平行四边形,
∴OB=OD(平行四边形对角线互相平分).
又∵AB∥CD,
∴∠EBO=∠FDO.
又∵ ∠EBO=∠DOF,
∴△BEO≌△DFO.
∴OE=OF.
分析:要证明OE=OF,只要证明它们所在的两个三角形全等即可.
新知讲解
例7 如图□ ABCD的对角线AC与BD相交于点O,其周长为16,且△AOB的周长比△BOC的周长小2.求边AB和BC的长.
解:∵四边形ABCD是平行四边形,
∴OA=OC(平行四边形对角线互相平分).
∵ △AOB的周+2= △BOC的周长,
∴AO+BO+AB+2=BO+CO+BC,
即 AB+2=BC.
又∵ □ ABCD的周长=16,
∴2(AB+BC)=16,
即4AB+4=16.
∴AB=3,BC=5.
新知讲解
例8 如图,在□ ABCD中,对角线AC=21cm,BE⊥AC,垂足为E ,且BE=5cm,AD=7cm.求AD和BC之间的距离.
解:设AD和BC之间的距离为x cm ,
则□ ABCD的面积等于AD·x.
∴AD·x=AC·BE,
即7x=21×5,
x=15(cm),
即AD和BC之间的距离为15cm.
新知讲解
边的运算
C
D
A
B
1、如图,在
ABCD中
A 基础知识:
(1)若AB=1㎝,BC=2 ㎝,
则
ABCD的周长=______.
6cm
(2)若AB=4㎝, BC=______.
ABCD的周长为 18,
5cm
B变式训练:
(1)若AB:BC=3:4,AB=6 ㎝,则BC=____,周长=_____.
8cm
28cm
(2)若AB:BC=3:4,周长为14㎝,则CD=——DA=——.
3cm
4cm
1.如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是______.
【解析】∵四边形ABCD是平行四边形,
∴AD BC,AB DC.
∵∠ABE=∠EBC,∴∠ABE=∠AEB,∴AB=AE.
又∵E是AD边上的中点,
∴AD=2AE=4,
∴平行四边形ABCD的周长为AB+BC+CD+AD=2+4+2+4=12.
答案:12
∥
=
∥
=
2.如图,在平面直角坐标系中,□ OBCD的顶点O,B,D的坐标如图所示,则顶点C的坐标为( )
x
y
C
O (0,0)
B(5,0)
D(2,3)
A. (3,7) B. (5,3) C. (7,3) D. (8,2)
C
角的运算
C
D
A
B
1、如图,在
ABCD中,
A:基础知识:
若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______.
50°
130°
50°
B:变式训练:
若∠A+ ∠C= 200°,则∠A=______ 、∠B=______.
100°
80°
2.如图,在□ ABCD中, ∠B=110°,延长AD至点F,延长CD至点E,连结EF,则∠E+∠F的值为( )
A.110° B.30° C.50° D.70°
【解析】选D.在□ABCD中,∠B=110°,∴∠ADC=∠B=110°,∴∠CDF=70°,由三角形外角的性质得,∠E+∠F=70°.
与对角线相关的运算
1、如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长以及□ ABCD的面积.
解:
∴△ABC是直角三角形,
又∵AC⊥BC,
∵四边形ABCD是平行四边形,
∴BC=AD=8,CD=AB=10.
又∵OA=OC ,∴
∴
∴S□ABCD= BC×AC=8×6=48。
8
10
B
C
D
A
●
O
2.如图,在□ ABCD中,AE⊥BD,∠EAD=60°,AE=2 cm,AC+BD=14 cm,则△OBC的周长是____cm.
【解析】在□ABCD中,BC=AD,OA=OC,OB=OD.
∵AE⊥BD,∠EAD=60°,AE=2 cm,∴AD=4 cm,BC=4cm.
∵AC+BD=14 cm,
∴OB+OC=7 (cm),
∴△OBC的周长为OB+OC+BC=11(cm).
答案:11
3.平行四边形ABCD的两条对角线相交于点O,OA,OB,AB的长度分别为3 cm,4 cm,5 cm,求其他各边以及两条对角线的长度.
【解】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,OB=OD.
又∵OA=3 cm,OB=4 cm,AB=5 cm,
∴AC=6 cm,BD=8 cm,CD=5 cm.
∵△AOB中,32+42=52,即AO2+BO2=AB2,
∴∠AOB=90°,∴AC⊥BD,
∴在Rt△AOD中,OA2+OD2=AD2,
∴AD=5 cm,BC=5 cm.
答:这个平行四边形的其他各边长都是5 cm,两条对角线长分别为6 cm和8 cm.
1.如图,在□ ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )
A.3 B.6
C.12 D.24
【解析】选C.观察图形会发现,每一小块阴影三角形都与它相对的三角形全等,则阴影部分的面积等于平行四边形面积的一半.故S阴影= = ×6×4=12.
与对称性相关的运算
1、【2019?贵州】如图,在□ABCD中,已知AC=4 cm,若△ACD的周长为13 cm,则□ABCD的周长为( )
A.26 cm B.24 cm C.20 cm D.18 cm
2、【2019?江苏】如图,在□ABCD中,∠A =70°,DC = DB ,则∠CDB =_________ .
3、【2019?湖北】如图,已知□ABCD的对角线AC、BD交于点O,且AC=8,BD=10,AB=5,则△OCD的周长为_________ .
D
40°
14
中考链接
平行四边形的性质
结论
对称性:平行四边形是中心对称图形;
性质定理1:平行四边形的对边平行且相等;
边
性质定理2:平行四边形的对角相等。
平行四边形邻边之和等于周长的一半。
平行四边形的邻角互补。
A
B
C
D
AD//BC;AB//DC
=
=
角
∠A=∠C;∠B=∠D
https://www.21cnjy.com/help/help_extract.php
华师大版 初中数学
18.1 平行四边形的性质
问题1:观察图形,说出下列图形边的位置有什么特征?
两组对边都不平行
一组对边平行
一组对边不平行
四边形
梯形
平行四边形
两组对边分别平行
你能举出日常生活中涉及的平行四边形吗?
思考
常见的平行四边形
生活中的平行四边形
新知导入
例如
平行四边形的定义:两组对边分别平行的四边形是平行四边形。
A
D
C
B
如图:四边形ABCD是平行四边形
记作:□ABCD
读作:平行四边形ABCD
温馨提示
(1)平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线;
(2)平行四边形相对的边称为对边;相对的角称为对角;
(3)平行四边形是特殊的四边形,特殊在两组对边分别平行哟!
平行四边形
按下面的步骤,在方格纸上画一个平行四边形。
m
A
B
C
D
n
(1)任意画一条直线m;
(2)在直线m上任取点A,在直线m外任取点B,连结AB;
(3)过点B作直线m的平行线n,在直线n上任取点C;
(4)过点C作直线AB的平行线,交直线m与点D,就得到□ABCD.
平行四边形除对边平行外,还有其他的性质吗?
平行四边形的画法
探索
按照下面步骤操作,思考并解决问题:
步骤1:在□ABCD中连接AC,BD,它们的交点为O;
步骤3:把两个平行四边形叠合在一起,用一枚图钉在O点穿过,将
□ABCD绕点O旋转180°;
步骤2:用剪刀把□ ABCD从方格纸上剪下,再在白纸上沿□ ABCD
的边沿,画一个四边形记为EFGH。
A
B
C
D
O
E
H
G
F
O
中心对称图形
AD=BC,AB=CD
∠BAD=∠BCD
∠ABC=∠ADC
平行四边形的对称性
探索
猜想:平行四边形的对边相等;平行四边形的对角相等。
A
B
C
D
已知:四边形ABCD是平行四边形
说明:AD=BC,AB=CD
∠BAD=∠BCD;∠ABC=∠ADC
1
2
3
4
BD=DB
∠1=∠2
∠3=∠4
思路解析
AD//BC
AB//CD
△ABD≌△CDB
∠A=∠C
AB=CD
AD=BC
思考
平行四边形的邻角有何关系呢?
平行四边形的性质
探索
问题:如图,在□ABCD中,当连结对角线AC、BD相交于点O时,除平行四边形中对边平行且相等、对角相等外,图中还有相等的线段吗?并说明理由。
A
B
C
D
O
O
发现
AO=CO,BO=DO
思考
(1)请你用演绎推理证明这个结论?
(2)你能归纳你得到的平行四边形的性质吗?
平行四边形对角线性质
思考
平行四边形的性质3:平行四边形的对角线互相平分。
A
B
C
D
O
几何语言
∴AO=CO,BO=DO
∵四边形ABCD是□
平行四边形的性质
例1 在□ABCD中,∠A=40 °,求其他各内角的大小.
解:在□ABCD中, ∠A=∠C,∠B=∠D(平行四边形的对角相等).
∵ ∠A=40°(已知),
∴ ∠C=40°.
又∵AD∥BC(平行四边形的对边平行),
∴∠A+∠B=180°(两直线平行,同旁内角互补).
∴∠B= 180 -∠A= 180?- 40°=140 °,
∠D= ∠B= 140 °.
新知讲解
例2 如图,在□ABCD中,AB=8,周长等于24.求其余三条边的长.
解: 在□ ABCD中,
AB=DC,AD=BC(平行四边形的对边相等).
∵AB=8,
∴DC=8,
又∵AB+BC+DC+AD=24,
∴ AD=BC= .
新知讲解
在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出平行线之间这些垂线段的长度.你能发现什么结论?试用平行四边形的性质定理加以说明.
两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离.
平行线之间的距离处处相等.
新知讲解
例3 已知平行四边形的周长是24,相邻两边的长度相差4,求该平行四边形相邻两边的长.
解:设AB的长为x,则BC的长为x+4.
根据已知,可得,
2(AB + BC)=24,即2(x +x +4)=24
4 x +8 =24,
解得x=4 .
所以,该平行四边形相邻两边的长分别为4和8 .
新知讲解
例4 已知:如图,在□ABCD中,∠ADC的平分线与AB相交于点E.求证:BE+BC=CD.
证明:∵四边形ABCD是平行四边形,
∴AB=CD(平行四边形的对边相等),
AB∥CD(平行四边形的对边平行),
∴∠CDE=∠AED.
又∵DE是∠ADC的平分线,
∴∠ADE=∠CDE, ∠ADE=∠AED,
∴AD=AE.
又∵AD=BC (平行四边形的对边相等),
∴ AE=BC.
BE+BC= BE+AE= CD.
新知讲解
例5 如图□ ABCD的对角线AC和 BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC与BD的和是多少?
解:在□ ABCD中
∵∴AB=6,AO+BO+AB=15,
∴AO+BO=15-6=9.
又∵AO=OC,BO=OD(平行四边形对角线互相平分),
∴AC+BD=2AO+2BO=2(AO+BO)=9×2=18.
新知讲解
例6 如图□ ABCD的对角线AC和BD相交于点O,EF过点O且与AB,CD相交于点E和点F.求证:OE=OF.
解:∵ABCD是平行四边形,
∴OB=OD(平行四边形对角线互相平分).
又∵AB∥CD,
∴∠EBO=∠FDO.
又∵ ∠EBO=∠DOF,
∴△BEO≌△DFO.
∴OE=OF.
分析:要证明OE=OF,只要证明它们所在的两个三角形全等即可.
新知讲解
例7 如图□ ABCD的对角线AC与BD相交于点O,其周长为16,且△AOB的周长比△BOC的周长小2.求边AB和BC的长.
解:∵四边形ABCD是平行四边形,
∴OA=OC(平行四边形对角线互相平分).
∵ △AOB的周+2= △BOC的周长,
∴AO+BO+AB+2=BO+CO+BC,
即 AB+2=BC.
又∵ □ ABCD的周长=16,
∴2(AB+BC)=16,
即4AB+4=16.
∴AB=3,BC=5.
新知讲解
例8 如图,在□ ABCD中,对角线AC=21cm,BE⊥AC,垂足为E ,且BE=5cm,AD=7cm.求AD和BC之间的距离.
解:设AD和BC之间的距离为x cm ,
则□ ABCD的面积等于AD·x.
∴AD·x=AC·BE,
即7x=21×5,
x=15(cm),
即AD和BC之间的距离为15cm.
新知讲解
边的运算
C
D
A
B
1、如图,在
ABCD中
A 基础知识:
(1)若AB=1㎝,BC=2 ㎝,
则
ABCD的周长=______.
6cm
(2)若AB=4㎝, BC=______.
ABCD的周长为 18,
5cm
B变式训练:
(1)若AB:BC=3:4,AB=6 ㎝,则BC=____,周长=_____.
8cm
28cm
(2)若AB:BC=3:4,周长为14㎝,则CD=——DA=——.
3cm
4cm
1.如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是______.
【解析】∵四边形ABCD是平行四边形,
∴AD BC,AB DC.
∵∠ABE=∠EBC,∴∠ABE=∠AEB,∴AB=AE.
又∵E是AD边上的中点,
∴AD=2AE=4,
∴平行四边形ABCD的周长为AB+BC+CD+AD=2+4+2+4=12.
答案:12
∥
=
∥
=
2.如图,在平面直角坐标系中,□ OBCD的顶点O,B,D的坐标如图所示,则顶点C的坐标为( )
x
y
C
O (0,0)
B(5,0)
D(2,3)
A. (3,7) B. (5,3) C. (7,3) D. (8,2)
C
角的运算
C
D
A
B
1、如图,在
ABCD中,
A:基础知识:
若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______.
50°
130°
50°
B:变式训练:
若∠A+ ∠C= 200°,则∠A=______ 、∠B=______.
100°
80°
2.如图,在□ ABCD中, ∠B=110°,延长AD至点F,延长CD至点E,连结EF,则∠E+∠F的值为( )
A.110° B.30° C.50° D.70°
【解析】选D.在□ABCD中,∠B=110°,∴∠ADC=∠B=110°,∴∠CDF=70°,由三角形外角的性质得,∠E+∠F=70°.
与对角线相关的运算
1、如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长以及□ ABCD的面积.
解:
∴△ABC是直角三角形,
又∵AC⊥BC,
∵四边形ABCD是平行四边形,
∴BC=AD=8,CD=AB=10.
又∵OA=OC ,∴
∴
∴S□ABCD= BC×AC=8×6=48。
8
10
B
C
D
A
●
O
2.如图,在□ ABCD中,AE⊥BD,∠EAD=60°,AE=2 cm,AC+BD=14 cm,则△OBC的周长是____cm.
【解析】在□ABCD中,BC=AD,OA=OC,OB=OD.
∵AE⊥BD,∠EAD=60°,AE=2 cm,∴AD=4 cm,BC=4cm.
∵AC+BD=14 cm,
∴OB+OC=7 (cm),
∴△OBC的周长为OB+OC+BC=11(cm).
答案:11
3.平行四边形ABCD的两条对角线相交于点O,OA,OB,AB的长度分别为3 cm,4 cm,5 cm,求其他各边以及两条对角线的长度.
【解】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,OB=OD.
又∵OA=3 cm,OB=4 cm,AB=5 cm,
∴AC=6 cm,BD=8 cm,CD=5 cm.
∵△AOB中,32+42=52,即AO2+BO2=AB2,
∴∠AOB=90°,∴AC⊥BD,
∴在Rt△AOD中,OA2+OD2=AD2,
∴AD=5 cm,BC=5 cm.
答:这个平行四边形的其他各边长都是5 cm,两条对角线长分别为6 cm和8 cm.
1.如图,在□ ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )
A.3 B.6
C.12 D.24
【解析】选C.观察图形会发现,每一小块阴影三角形都与它相对的三角形全等,则阴影部分的面积等于平行四边形面积的一半.故S阴影= = ×6×4=12.
与对称性相关的运算
1、【2019?贵州】如图,在□ABCD中,已知AC=4 cm,若△ACD的周长为13 cm,则□ABCD的周长为( )
A.26 cm B.24 cm C.20 cm D.18 cm
2、【2019?江苏】如图,在□ABCD中,∠A =70°,DC = DB ,则∠CDB =_________ .
3、【2019?湖北】如图,已知□ABCD的对角线AC、BD交于点O,且AC=8,BD=10,AB=5,则△OCD的周长为_________ .
D
40°
14
中考链接
平行四边形的性质
结论
对称性:平行四边形是中心对称图形;
性质定理1:平行四边形的对边平行且相等;
边
性质定理2:平行四边形的对角相等。
平行四边形邻边之和等于周长的一半。
平行四边形的邻角互补。
A
B
C
D
AD//BC;AB//DC
=
=
角
∠A=∠C;∠B=∠D
https://www.21cnjy.com/help/help_extract.php
