16.2 动量和动量定理 (共36张PPT)
文档属性
| 名称 | 16.2 动量和动量定理 (共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 813.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-02 09:48:07 | ||
图片预览











文档简介
(共36张PPT)
16.2 动量和动量定理
一、动量
1、定义:物体的质量与速度的乘积叫做物体的动量。符号:p。
p=mv。
m:物体的质量;V:物体的瞬时速度。
单位:kg?m/s。
2、物理意义:动量是从动力学的角度描述物体运动状态的物理量。
比较描述物理运动状态的三个量:V、P、Ek。
3、动量的性质:
⑴动量是矢量:某时刻动量的方向与该时刻速度方向相同。
⑵动量是状态量:即动量是物体在某时刻或某位置上的物理量。
⑶动量具有相对性:选取不同的参考系,物体的速度不同,物体的动量也不同。高中阶段均以地面为参考系来确定物体的动量。
问题:试比较一下动量和动能的关系。
①动量和动能都是描述物体运动的状态量。动量是从动力学角度;动能则是从能量的角度。
②动量是矢量,动能是标量
③定量关系:
例题1:关于物体的动能与动量的说法,正确的有:( )
A、物体的动能发生变化时,物体的动量一定变化。
B、物体的动量发生变化时,物体的动能一定变化。
C、物体所受合外力不为零时,物体的动量一定变化。
D、合外力对物体不做功时或做功的代数和为零时,物体的动量不变。
E、物体的动量不变时,物体所受的合外力一定为零。
ACE
3、动量的变化:
⑴、定义:某段时间内,末动量减初动量叫做物体在该段时间内动量的变化。符号:Δp
Δp= pt-p0= m(vt-v0)= mΔv。
⑵理解:
①Δp为 pt、p0的矢量差。
当vt、v0 在同一直线上时,规定正方向后,Δp=pt-p0为代数和的形式。
当vt、v0 不在同一直线上时,必须利用平行四边形定则求解。
②动量的变化也是矢量,求动量的变化时,不仅要确定大小,还要确定方向, Δp的方向与Δv的方向一致。
例题2:求下列碰撞中,小球动量的变化。
⑴质量m=0.1kg的小球,以v0=8m/s的速度向北运动,与在运动方向上的另一小球碰撞后,以6m/s的速度继续向北运动。
⑵质量m=0.1kg的小球,以v0=8m/s的速度向北运动,与在运动方向上的另一小球碰撞后,以6m/s的速度向南运动。
⑶质量m=0.1kg的小球,以v0=8m/s的速度向北运动,与在运动方向上的另一小球碰撞后,以6m/s的速度向西运动。
⑷质量m=0.1kg的小球,以v0=8m/s的速度向北运动,与在运动方向上的另一小球碰撞后,以5m/s的速度向东偏南530方向运动。
ΔP=0.2kg · m/s,向南
ΔP=1.4kg · m/s,向南
ΔP=1.0kg · m/s,西偏南530
ΔP=3√17kg · m/s,南偏东θ,tanθ=1/4
二、冲量
1、定义:力与力的作用时间的乘积叫做力的冲量。符号:I。
定义式: I=Ft;单位:N?s。
2、冲量的性质
⑴冲量是矢量,当力的方向不变时,冲量的方向与力的方向相同;当力的方向改变时,冲量的方向与对应过程中速度变化的方向相同。
⑵冲量是过程量,冲量是力对时间的累积效应。
注:力作用在物体上的三种作用效果:力产生加速度;力对物体做的功;对物体的冲量。
3、冲量的计算
⑴恒力冲量的计算:I=Ft,方向与F同向
⑵变力冲量的求解:
方法一:微元法:
将力作用时间分割成许多微小的时间间隔,在每个微小的时间内,将力看作恒力,先求出各微小的时间内力的冲量再求各冲量的矢量和。
方法二:利用动量定理间接求解法。
⑶特殊变力的冲量:
当力的方向不变,而力的大小随时间均匀变化。
I=F平t=(Ft+F0)t/2
例题3:从同一高度以相同的速率抛出质量相同的三个小球,a球竖直上抛,b球竖直下抛,c球水平抛出,不计空气阻力,下列说法中正确的是:( )
A、三球落地时的动量相同。
B、三球落地时的动能相同。
C、运动过程中,三球受到的冲量相同。
D、运动过程中,三球动量变化的大小相同。
B
主意动量大小的变化和动量变化的大小的区别
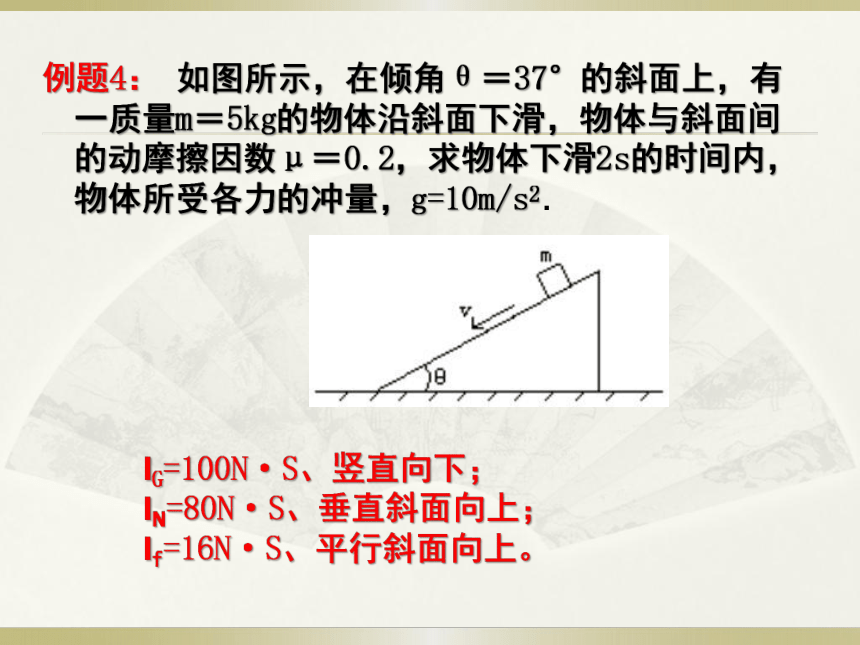
例题4: 如图所示,在倾角θ=37°的斜面上,有一质量m=5kg的物体沿斜面下滑,物体与斜面间的动摩擦因数μ=0.2,求物体下滑2s的时间内,物体所受各力的冲量,g=10m/s2.
IG=100N·S、竖直向下;
IN=80N·S、垂直斜面向上;
If=16N·S、平行斜面向上。
三、动量定理:
1、动量定理的推导:
(学生根据牛顿第二定律推导出动量定理)
2、动量定理:
在任意过程中,物体动量的变化等于在这一过程中所受的合外力的冲量。
3、对定理的理解
⑴动量定理对任意过程的都成立,即不管过程中物体如何运动,受恒力还是变力,受多少个力,单一过程还是多阶段组成的复杂过程。
⑵动量定理的表达式是一个矢量方程,方程两边不仅大小相等,方向也相同。对作用前后在同一直线上的问题,列方程时必须规定好矢量的正方向。
⑶动量定理的研究对象可以是单个的物体,也可以是多个物体组成的系统(各物体的速度可不同)。由于内力总是成对出现,产生的冲量总是等大反向的。故系统内相互作用的内力产生冲量矢量和一定为零。系统动量的变化也只决定于系统所受合外力的冲量。
4、牛顿第二定律、动能定理、动量定理三个规律的比较。
牛二定律 动能定理 动量定理
方程 F合=ma F合S cosθ=Ekt-Ek0 F合t=Pt-P0
方程性质 矢量方程
瞬时方程 标量方程
过程方程 矢量方程
过程方程
研究对象 单个物体
(高中) 单个物体
(高中) 单个物体
或物体系
适用条件 低速运动
宏观物体 低速运动
宏观物体 各种情况
例题5:物体在运动过程中只受到力F的作用,F随时间变化的图象如图所示,已知在t=1 s时刻,物体的速度为零.则下列论述错误的是:( )
A.0~3s内,力F所做的功等
于零,冲量也等于零。
B.0~4s内,力F所做的功等
于零,冲量也等于零。
C.第1s内和第2s内的速度方向
相同,加速度方向相反。
D.第3s内和第4s内的速度方向
相同,加速度方向相同。
B
例题6:物体的质量为m=2.5 kg,静止在水平地面上。物体与地面间滑动摩擦系数μ=0.2,物体受到与地面平行的拉力F作用,F方向不变,大小随时间变化规律如图所示,那么下述判断正确的是:( )
A、前2 s物体静止不动,因拉力F小于摩擦力
B、6 s内,拉力F对物体的冲量大小等于50N·s
C、6 s内,摩擦力对物体的冲量大小等于30N·s
D、6 s末物体的速度大小是12m/s
D
三、动量定理的应用
1、用动量定理定性的解析物理现象
⑴由动量定理:Ft=ΔP有:F= ΔP/ t。当物体的动量变化一定时,作用时间t越长,F越小;作用时间越短,作用力越大。
⑵由动量定理: ΔP=Ft,可知作用力一定时,t越大, ΔP越大,物体动量的变化越大,对原来的静止的物体获得的速度越大。
注:作用时间的长短与作用过程中物体的形变大小有关。同一物体,形变越大作用时间越长;形变越小,作用时间越短。
例题7:请用动量定理解析下列现象:
⑴ 玻璃器皿掉在水泥地上易碎,而掉在泥地上不易碎。
⑵搬运电器和易碎品时,为什么都要用泡沫塑料进行包装。
⑶气功表演中,在人的身上放置大石板,用大锤猛砸石板,石板被打碎,而人安然无恙。
⑷篮球运动员接球时,手为什么要顺势收回?足球运动员可头顶球,能否用头顶在空中运动的铅球。
⑸在水平桌面上放一纸带,在纸带上一砝码,缓慢拉动纸带时,砝码会掉在地面上,迅速抽动纸带,砝码在几乎不动。
动画:足球与铅球
例题8:如图所示,用两根完全相同的细绳系在一重球上,并将球悬挂在天花板上。当用力缓慢拉球下面的细绳时,上、下那根细绳会断?若用力迅猛拉下端细绳时,又是那根的细绳被拉断?并解析这种现象。
2、用动量定理进行定量求解问题
应用动量定理解题的基本步骤:
第一步:选择研究对象。
动量定律的研究对象可以是单个的物体,也可以是几个物体组成的物体系
第二步:选择研究过程,确定过程的初、末状态,并求出初、末状态物体的动量。
研究过程可以是单一的过程,也可以是多个阶段组成的复合过程。
第三步:分析物体的受力情况,求出各力的冲量。
对物体系,只需分析物体系所受的外力,求外力的冲量,与内力及其冲量无关。
第四步:选取正方向,根据动量定理列方程。
动量定理的表达式:
单个物体单一过程:
单个物体多阶段的过程:
多个物体组成的物体系:
第五步:根据题意,列出辅助方程。
第六步:解方程组求解未知量。
注:⑴对作用时间极短、作用力很大的:打击、碰撞、爆炸等过程,重力的冲量可忽略不计。
⑵对方向未知量,均先假定为正方向,最后根据结果的正负判断具体的方向。
例题9:质量为m的运动员从下蹲状态向上起跳,经Δt时间身体伸直并刚好以速度v离开地面,设此人在起跳过程中,重心升高了h。求此在此过程中地面对运动员的冲量和地面对他做的功。
I=mv+mgΔt;W=0
题型一:单个物体
例题10:质量为4kg的小球,从h1=3.2m高处自由下落,掉到水平地板上后,弹起的高度为1.8m。已知小球从开始下落到弹到最高点所经历的时间t=1.5s,g取10m/s2。求小球与地板碰撞时,对地板弹力有多大?
FN=600N
例题11:如图所示,质量为m=2 kg的物体,在水平力F=16 N的作用下,由静止开始沿水平面向右运动。已知物体与水平面间的动摩擦因数μ=0.2.若F作用t1=2 s后撤去,撤去F后又经t2=2 s物体与竖直墙壁相碰,若物体与墙壁作用时间t3=0.1 s,碰撞后反向弹回的速度v=6 m/s,求墙壁对物体的平均作用力.(g取10 m/s2)
F=280N
例题12:水平推力F1和F2(F1>F2)分别作用在置于同一水平地面上完全相同的两个物体上,使两物体由静止开始运动。F1和F2各自作用一段时间后撤去,两物体最终都停止运动。如果两物体运动过程中的位移相同,两次相比较下列说法中正确的是:( )
A、F1 的冲量较大。
B、F1 做的功较多。
C、推力F2那次,摩擦力的冲量较大。
D、推力F2那次,物体获得的最大速度较大。
C
例题13:如图所示,质量分别为mA=2kg、 mB=1kg的A、B两物体,相隔一定的距离。已知两物体与水平地面之间的动摩擦因素均为0.1。A物体以10m/s的水平初速度。向静止的B物体运动,A、B碰撞后分开以不同的速度均向右运动,已知A物体碰前、后运动的总时间为6s,若不计碰撞时间,g=10m/s2。求碰后B物体的运动时间。
tB=8s
题型二:物体系
13、解:因碰撞过程中系统无动量损失,整个过程中,系统动量的变化等于A、B两物体所受摩擦力的冲量。取向右为正方向,对A、B组成的系统,在全过程中由动量定理有:
- μAmAtA - μBmBtB= 0 -mAV0。
解得:tB=8s
例题14:用细线将质量分别为M、m的金属块与木块连在一起浸在水中,开始时木块的上表面刚好与水面相平,如图所示。现从静止释放后,系统以加速度a加速下沉,经t1时间细线突然断裂,又经t2时间木块回到初始位置,且具有向上的速度v。求此时金属块的速度。
14、解:取向下为正方向,
对两物体组成的系统所受的合外力:
F=(M+m)a
对整个过程由系统的动量动量有:
F(t1+t2)=(MVM-mV)-0
故有:
例题15:高压采煤水枪出水口的截面积为s,喷出水的速度为v,水的密度为ρ。若水枪正对着煤层近距离喷射,且假设水射到煤层上后速度变为零。求水对煤层的冲击力。
题型三:流体
例题16:一股水流以10m/s的速度从水枪的喷嘴喷出,喷嘴的截面积为0.5cm2。有一质量为0.32kg的球,因水对其下侧的冲击而悬空。假设水全部冲击到小球上,且冲击后水的速度变为零。求小球因水的冲击悬停在离喷嘴多高处。
h=2.95m
方法归纳:
⑴基本方法:用动量定理解决流体问题,一般采用微元法:即:取一个很短时间Δt,对Δt内流出液体Δm用动量定理。
⑵解题的关键:
①确定Δm与Δt、液体的速度、密度等的关系。
②确定Δm作用前后速度的变化。
③ Δt趋近零时, Δm很小,所受的重力均不计。
⑶特点:⑴对水枪喷射问题,当空中水柱稳定后,空中水的体积不变,任何时间内从枪口射出的水等于射向墙壁或物体的水。
⑵若水柱不散开,水柱的横截面积与水的速度成反比。
例题17:如图所示,自动称米机已在许多大粮店广泛使用.买者认为:因为米流落到容器中时对容器有向下的冲力而不划算;卖者则认为:当预定米的质量达到要求时,自动装置即刻切断米流,此刻有一些米仍在空中,这些米是多给买者的,因而双方争执起来.下列说法正确的是( )
A.买者说的对
B.卖者说的对
C.公平交易
D.具有随机性,无法判断
C
解:设米流的流量为q,它是恒定的,米流在出口处速度很小可视为零,若切断米流后,设盛米的容器中静止的那部分米的质量为m1,空中还在下落的米的质量为m2,落到已静止的米堆上的一小部分米的质量为Δm。在极短 时间Δt内,取Δm为研究对象,这部分米很少,Δm=q·Δt,设其落到米堆上之前的速度为v,经Δt时间静止,如图所示,取竖直向上为正方向,由动量定理得(F-Δmg)Δt=Δmv,F=qv+q·Δt·g,因Δt很小,故F=qv,根据牛顿第三定律知F=F′,称米机的读数应为M=(m1g+F′ )/g=m1+qv/g,因切断米流后空中尚有t=v/g时间内对应的米流在空中,故qv/g=m2,可见,称米机读数包含了静止在
袋中的那部分米的质量m1,也包含了尚在空中
的下落的米的质量m2,即自动称米机是准确的。
例题18:一艘帆船在静水中由于风力的推动做匀速直线运动,风帆的面积为S,风速为V0,空气的密度为ρ。若帆船在水中航行受到水的阻力与帆船在水中航行的速度成正比,比例系数为k。试确定帆船航行的速度V与S、V、ρ、k的关系式。
例题19:一密闭的真空容器,上面有一个面积很小的装有阀门k的进气孔,如图所示。已知容器所在空间的大气压为p,空气密度为ρ。求打开滑门的瞬间,空气进入容器的速度。
例题20:如图所示,一根长度为L,质量为m的粗细均匀的柔软的细绳,堆放在水平桌面上,现用手提起细绳的一端,使绳子竖直向上以速度V匀速运动。求当所提端离水平面的距离为x(x
16.2 动量和动量定理
一、动量
1、定义:物体的质量与速度的乘积叫做物体的动量。符号:p。
p=mv。
m:物体的质量;V:物体的瞬时速度。
单位:kg?m/s。
2、物理意义:动量是从动力学的角度描述物体运动状态的物理量。
比较描述物理运动状态的三个量:V、P、Ek。
3、动量的性质:
⑴动量是矢量:某时刻动量的方向与该时刻速度方向相同。
⑵动量是状态量:即动量是物体在某时刻或某位置上的物理量。
⑶动量具有相对性:选取不同的参考系,物体的速度不同,物体的动量也不同。高中阶段均以地面为参考系来确定物体的动量。
问题:试比较一下动量和动能的关系。
①动量和动能都是描述物体运动的状态量。动量是从动力学角度;动能则是从能量的角度。
②动量是矢量,动能是标量
③定量关系:
例题1:关于物体的动能与动量的说法,正确的有:( )
A、物体的动能发生变化时,物体的动量一定变化。
B、物体的动量发生变化时,物体的动能一定变化。
C、物体所受合外力不为零时,物体的动量一定变化。
D、合外力对物体不做功时或做功的代数和为零时,物体的动量不变。
E、物体的动量不变时,物体所受的合外力一定为零。
ACE
3、动量的变化:
⑴、定义:某段时间内,末动量减初动量叫做物体在该段时间内动量的变化。符号:Δp
Δp= pt-p0= m(vt-v0)= mΔv。
⑵理解:
①Δp为 pt、p0的矢量差。
当vt、v0 在同一直线上时,规定正方向后,Δp=pt-p0为代数和的形式。
当vt、v0 不在同一直线上时,必须利用平行四边形定则求解。
②动量的变化也是矢量,求动量的变化时,不仅要确定大小,还要确定方向, Δp的方向与Δv的方向一致。
例题2:求下列碰撞中,小球动量的变化。
⑴质量m=0.1kg的小球,以v0=8m/s的速度向北运动,与在运动方向上的另一小球碰撞后,以6m/s的速度继续向北运动。
⑵质量m=0.1kg的小球,以v0=8m/s的速度向北运动,与在运动方向上的另一小球碰撞后,以6m/s的速度向南运动。
⑶质量m=0.1kg的小球,以v0=8m/s的速度向北运动,与在运动方向上的另一小球碰撞后,以6m/s的速度向西运动。
⑷质量m=0.1kg的小球,以v0=8m/s的速度向北运动,与在运动方向上的另一小球碰撞后,以5m/s的速度向东偏南530方向运动。
ΔP=0.2kg · m/s,向南
ΔP=1.4kg · m/s,向南
ΔP=1.0kg · m/s,西偏南530
ΔP=3√17kg · m/s,南偏东θ,tanθ=1/4
二、冲量
1、定义:力与力的作用时间的乘积叫做力的冲量。符号:I。
定义式: I=Ft;单位:N?s。
2、冲量的性质
⑴冲量是矢量,当力的方向不变时,冲量的方向与力的方向相同;当力的方向改变时,冲量的方向与对应过程中速度变化的方向相同。
⑵冲量是过程量,冲量是力对时间的累积效应。
注:力作用在物体上的三种作用效果:力产生加速度;力对物体做的功;对物体的冲量。
3、冲量的计算
⑴恒力冲量的计算:I=Ft,方向与F同向
⑵变力冲量的求解:
方法一:微元法:
将力作用时间分割成许多微小的时间间隔,在每个微小的时间内,将力看作恒力,先求出各微小的时间内力的冲量再求各冲量的矢量和。
方法二:利用动量定理间接求解法。
⑶特殊变力的冲量:
当力的方向不变,而力的大小随时间均匀变化。
I=F平t=(Ft+F0)t/2
例题3:从同一高度以相同的速率抛出质量相同的三个小球,a球竖直上抛,b球竖直下抛,c球水平抛出,不计空气阻力,下列说法中正确的是:( )
A、三球落地时的动量相同。
B、三球落地时的动能相同。
C、运动过程中,三球受到的冲量相同。
D、运动过程中,三球动量变化的大小相同。
B
主意动量大小的变化和动量变化的大小的区别
例题4: 如图所示,在倾角θ=37°的斜面上,有一质量m=5kg的物体沿斜面下滑,物体与斜面间的动摩擦因数μ=0.2,求物体下滑2s的时间内,物体所受各力的冲量,g=10m/s2.
IG=100N·S、竖直向下;
IN=80N·S、垂直斜面向上;
If=16N·S、平行斜面向上。
三、动量定理:
1、动量定理的推导:
(学生根据牛顿第二定律推导出动量定理)
2、动量定理:
在任意过程中,物体动量的变化等于在这一过程中所受的合外力的冲量。
3、对定理的理解
⑴动量定理对任意过程的都成立,即不管过程中物体如何运动,受恒力还是变力,受多少个力,单一过程还是多阶段组成的复杂过程。
⑵动量定理的表达式是一个矢量方程,方程两边不仅大小相等,方向也相同。对作用前后在同一直线上的问题,列方程时必须规定好矢量的正方向。
⑶动量定理的研究对象可以是单个的物体,也可以是多个物体组成的系统(各物体的速度可不同)。由于内力总是成对出现,产生的冲量总是等大反向的。故系统内相互作用的内力产生冲量矢量和一定为零。系统动量的变化也只决定于系统所受合外力的冲量。
4、牛顿第二定律、动能定理、动量定理三个规律的比较。
牛二定律 动能定理 动量定理
方程 F合=ma F合S cosθ=Ekt-Ek0 F合t=Pt-P0
方程性质 矢量方程
瞬时方程 标量方程
过程方程 矢量方程
过程方程
研究对象 单个物体
(高中) 单个物体
(高中) 单个物体
或物体系
适用条件 低速运动
宏观物体 低速运动
宏观物体 各种情况
例题5:物体在运动过程中只受到力F的作用,F随时间变化的图象如图所示,已知在t=1 s时刻,物体的速度为零.则下列论述错误的是:( )
A.0~3s内,力F所做的功等
于零,冲量也等于零。
B.0~4s内,力F所做的功等
于零,冲量也等于零。
C.第1s内和第2s内的速度方向
相同,加速度方向相反。
D.第3s内和第4s内的速度方向
相同,加速度方向相同。
B
例题6:物体的质量为m=2.5 kg,静止在水平地面上。物体与地面间滑动摩擦系数μ=0.2,物体受到与地面平行的拉力F作用,F方向不变,大小随时间变化规律如图所示,那么下述判断正确的是:( )
A、前2 s物体静止不动,因拉力F小于摩擦力
B、6 s内,拉力F对物体的冲量大小等于50N·s
C、6 s内,摩擦力对物体的冲量大小等于30N·s
D、6 s末物体的速度大小是12m/s
D
三、动量定理的应用
1、用动量定理定性的解析物理现象
⑴由动量定理:Ft=ΔP有:F= ΔP/ t。当物体的动量变化一定时,作用时间t越长,F越小;作用时间越短,作用力越大。
⑵由动量定理: ΔP=Ft,可知作用力一定时,t越大, ΔP越大,物体动量的变化越大,对原来的静止的物体获得的速度越大。
注:作用时间的长短与作用过程中物体的形变大小有关。同一物体,形变越大作用时间越长;形变越小,作用时间越短。
例题7:请用动量定理解析下列现象:
⑴ 玻璃器皿掉在水泥地上易碎,而掉在泥地上不易碎。
⑵搬运电器和易碎品时,为什么都要用泡沫塑料进行包装。
⑶气功表演中,在人的身上放置大石板,用大锤猛砸石板,石板被打碎,而人安然无恙。
⑷篮球运动员接球时,手为什么要顺势收回?足球运动员可头顶球,能否用头顶在空中运动的铅球。
⑸在水平桌面上放一纸带,在纸带上一砝码,缓慢拉动纸带时,砝码会掉在地面上,迅速抽动纸带,砝码在几乎不动。
动画:足球与铅球
例题8:如图所示,用两根完全相同的细绳系在一重球上,并将球悬挂在天花板上。当用力缓慢拉球下面的细绳时,上、下那根细绳会断?若用力迅猛拉下端细绳时,又是那根的细绳被拉断?并解析这种现象。
2、用动量定理进行定量求解问题
应用动量定理解题的基本步骤:
第一步:选择研究对象。
动量定律的研究对象可以是单个的物体,也可以是几个物体组成的物体系
第二步:选择研究过程,确定过程的初、末状态,并求出初、末状态物体的动量。
研究过程可以是单一的过程,也可以是多个阶段组成的复合过程。
第三步:分析物体的受力情况,求出各力的冲量。
对物体系,只需分析物体系所受的外力,求外力的冲量,与内力及其冲量无关。
第四步:选取正方向,根据动量定理列方程。
动量定理的表达式:
单个物体单一过程:
单个物体多阶段的过程:
多个物体组成的物体系:
第五步:根据题意,列出辅助方程。
第六步:解方程组求解未知量。
注:⑴对作用时间极短、作用力很大的:打击、碰撞、爆炸等过程,重力的冲量可忽略不计。
⑵对方向未知量,均先假定为正方向,最后根据结果的正负判断具体的方向。
例题9:质量为m的运动员从下蹲状态向上起跳,经Δt时间身体伸直并刚好以速度v离开地面,设此人在起跳过程中,重心升高了h。求此在此过程中地面对运动员的冲量和地面对他做的功。
I=mv+mgΔt;W=0
题型一:单个物体
例题10:质量为4kg的小球,从h1=3.2m高处自由下落,掉到水平地板上后,弹起的高度为1.8m。已知小球从开始下落到弹到最高点所经历的时间t=1.5s,g取10m/s2。求小球与地板碰撞时,对地板弹力有多大?
FN=600N
例题11:如图所示,质量为m=2 kg的物体,在水平力F=16 N的作用下,由静止开始沿水平面向右运动。已知物体与水平面间的动摩擦因数μ=0.2.若F作用t1=2 s后撤去,撤去F后又经t2=2 s物体与竖直墙壁相碰,若物体与墙壁作用时间t3=0.1 s,碰撞后反向弹回的速度v=6 m/s,求墙壁对物体的平均作用力.(g取10 m/s2)
F=280N
例题12:水平推力F1和F2(F1>F2)分别作用在置于同一水平地面上完全相同的两个物体上,使两物体由静止开始运动。F1和F2各自作用一段时间后撤去,两物体最终都停止运动。如果两物体运动过程中的位移相同,两次相比较下列说法中正确的是:( )
A、F1 的冲量较大。
B、F1 做的功较多。
C、推力F2那次,摩擦力的冲量较大。
D、推力F2那次,物体获得的最大速度较大。
C
例题13:如图所示,质量分别为mA=2kg、 mB=1kg的A、B两物体,相隔一定的距离。已知两物体与水平地面之间的动摩擦因素均为0.1。A物体以10m/s的水平初速度。向静止的B物体运动,A、B碰撞后分开以不同的速度均向右运动,已知A物体碰前、后运动的总时间为6s,若不计碰撞时间,g=10m/s2。求碰后B物体的运动时间。
tB=8s
题型二:物体系
13、解:因碰撞过程中系统无动量损失,整个过程中,系统动量的变化等于A、B两物体所受摩擦力的冲量。取向右为正方向,对A、B组成的系统,在全过程中由动量定理有:
- μAmAtA - μBmBtB= 0 -mAV0。
解得:tB=8s
例题14:用细线将质量分别为M、m的金属块与木块连在一起浸在水中,开始时木块的上表面刚好与水面相平,如图所示。现从静止释放后,系统以加速度a加速下沉,经t1时间细线突然断裂,又经t2时间木块回到初始位置,且具有向上的速度v。求此时金属块的速度。
14、解:取向下为正方向,
对两物体组成的系统所受的合外力:
F=(M+m)a
对整个过程由系统的动量动量有:
F(t1+t2)=(MVM-mV)-0
故有:
例题15:高压采煤水枪出水口的截面积为s,喷出水的速度为v,水的密度为ρ。若水枪正对着煤层近距离喷射,且假设水射到煤层上后速度变为零。求水对煤层的冲击力。
题型三:流体
例题16:一股水流以10m/s的速度从水枪的喷嘴喷出,喷嘴的截面积为0.5cm2。有一质量为0.32kg的球,因水对其下侧的冲击而悬空。假设水全部冲击到小球上,且冲击后水的速度变为零。求小球因水的冲击悬停在离喷嘴多高处。
h=2.95m
方法归纳:
⑴基本方法:用动量定理解决流体问题,一般采用微元法:即:取一个很短时间Δt,对Δt内流出液体Δm用动量定理。
⑵解题的关键:
①确定Δm与Δt、液体的速度、密度等的关系。
②确定Δm作用前后速度的变化。
③ Δt趋近零时, Δm很小,所受的重力均不计。
⑶特点:⑴对水枪喷射问题,当空中水柱稳定后,空中水的体积不变,任何时间内从枪口射出的水等于射向墙壁或物体的水。
⑵若水柱不散开,水柱的横截面积与水的速度成反比。
例题17:如图所示,自动称米机已在许多大粮店广泛使用.买者认为:因为米流落到容器中时对容器有向下的冲力而不划算;卖者则认为:当预定米的质量达到要求时,自动装置即刻切断米流,此刻有一些米仍在空中,这些米是多给买者的,因而双方争执起来.下列说法正确的是( )
A.买者说的对
B.卖者说的对
C.公平交易
D.具有随机性,无法判断
C
解:设米流的流量为q,它是恒定的,米流在出口处速度很小可视为零,若切断米流后,设盛米的容器中静止的那部分米的质量为m1,空中还在下落的米的质量为m2,落到已静止的米堆上的一小部分米的质量为Δm。在极短 时间Δt内,取Δm为研究对象,这部分米很少,Δm=q·Δt,设其落到米堆上之前的速度为v,经Δt时间静止,如图所示,取竖直向上为正方向,由动量定理得(F-Δmg)Δt=Δmv,F=qv+q·Δt·g,因Δt很小,故F=qv,根据牛顿第三定律知F=F′,称米机的读数应为M=(m1g+F′ )/g=m1+qv/g,因切断米流后空中尚有t=v/g时间内对应的米流在空中,故qv/g=m2,可见,称米机读数包含了静止在
袋中的那部分米的质量m1,也包含了尚在空中
的下落的米的质量m2,即自动称米机是准确的。
例题18:一艘帆船在静水中由于风力的推动做匀速直线运动,风帆的面积为S,风速为V0,空气的密度为ρ。若帆船在水中航行受到水的阻力与帆船在水中航行的速度成正比,比例系数为k。试确定帆船航行的速度V与S、V、ρ、k的关系式。
例题19:一密闭的真空容器,上面有一个面积很小的装有阀门k的进气孔,如图所示。已知容器所在空间的大气压为p,空气密度为ρ。求打开滑门的瞬间,空气进入容器的速度。
例题20:如图所示,一根长度为L,质量为m的粗细均匀的柔软的细绳,堆放在水平桌面上,现用手提起细绳的一端,使绳子竖直向上以速度V匀速运动。求当所提端离水平面的距离为x(x
