青岛版八年级下册6.3 特殊的平行四边形(4)菱形的判定定理课件(共15张PPT)
文档属性
| 名称 | 青岛版八年级下册6.3 特殊的平行四边形(4)菱形的判定定理课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-02 10:06:59 | ||
图片预览




文档简介
(共15张PPT)
第6章 平行四边形
6.3 特殊的平行四边形(4)
——菱形的判定定理
A
D
C
B
O
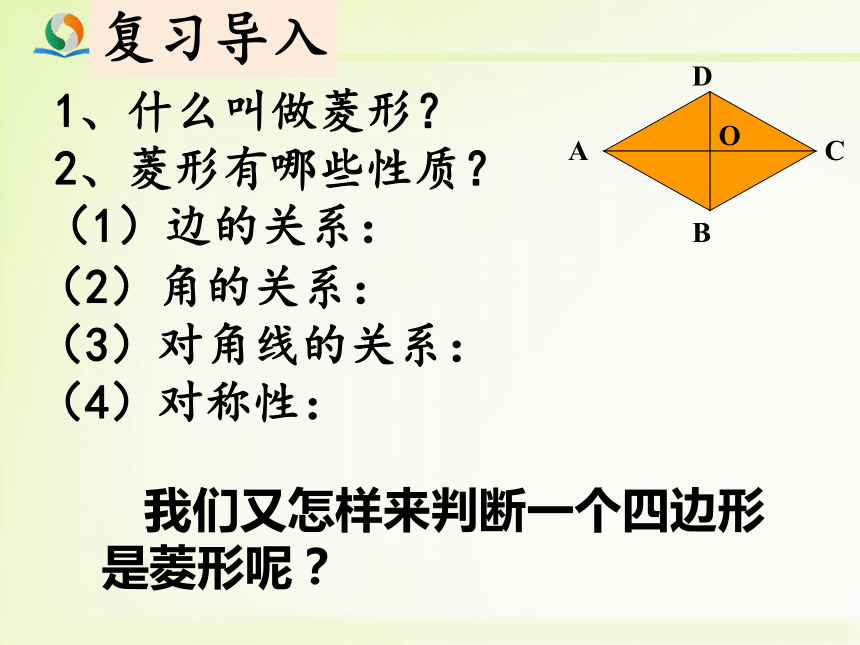
复习导入
1、什么叫做菱形?
2、菱形有哪些性质?
(1)边的关系:
(2)角的关系:
(3)对角线的关系:
(4)对称性:
我们又怎样来判断一个四边形
是菱形呢?
1、定义法:
一组邻边相等的平行四边形是菱形。
三、菱形的判定方法
A
B
C
D
几何语言
∵四边形ABCD是
平行四边形
AB=BC
∴四边形ABCD是菱形
A
B
C
D
探索(一)
已知:在四边形ABCD中,AB=BC
=CD=DA.
求证:四边形ABCD是菱形。
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
1、定义法:
三、菱形的判定方法
2、判定定理1
有四条边相等的四边形是菱形.
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
几何语言
A
B
C
D
O
∟
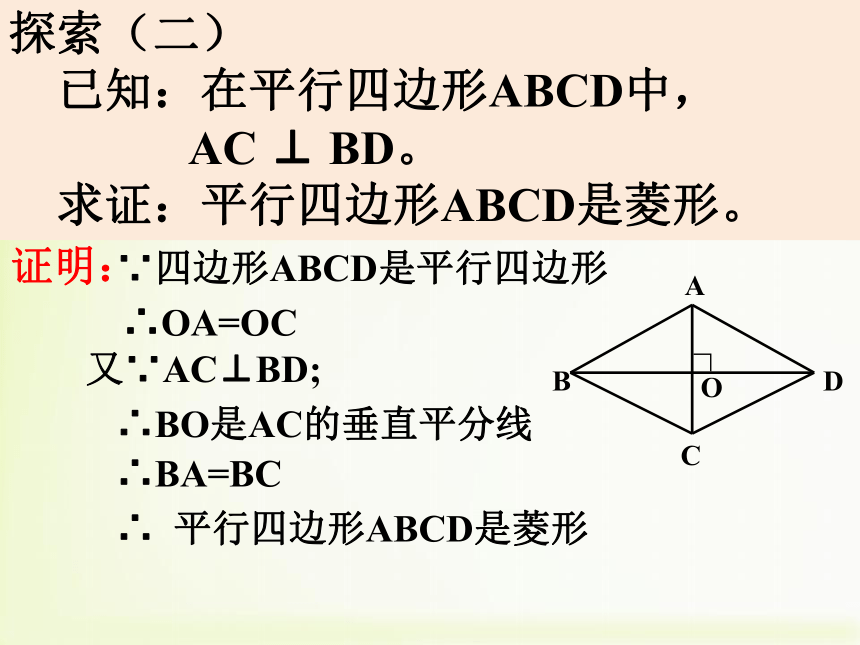
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴ 平行四边形ABCD是菱形
探索(二)
已知:在平行四边形ABCD中,
AC ⊥ BD。
求证:平行四边形ABCD是菱形。
∴BO是AC的垂直平分线
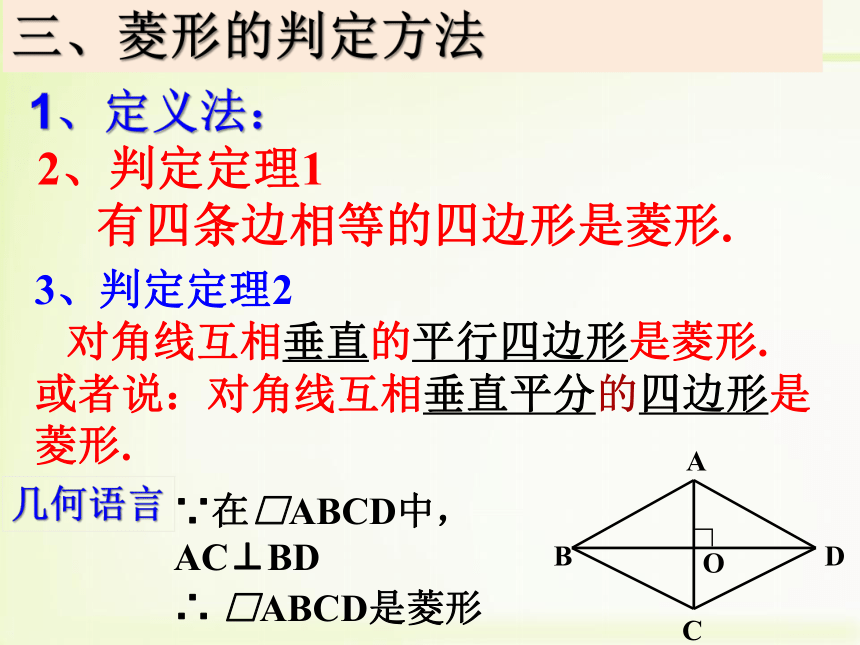
3、判定定理2
对角线互相垂直的平行四边形是菱形.
1、定义法:
三、菱形的判定方法
2、判定定理1
有四条边相等的四边形是菱形.
A
B
C
D
O
∟
几何语言
∵在□ABCD中,
AC⊥BD
∴ □ABCD是菱形
或者说:对角线互相垂直平分的四边形是菱形.
例题精讲
例1.已知:如图,CE是△ABC的外角
∠ACD的平分线,AF∥CD交CE
于点F,FG∥AC交CD于点G.
求证:四边形ACGF是菱形。
A
B
C
D
E
F
G
1
2
3
4
例2、已知:AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F,求证:四边形AEDF是菱形。
例题精讲
A
B
C
D
E
F
1
2
3
4
例3、已知:AD是△ABC的角平分线,点E、F分别在边AB、AC上,且EF垂直平分AD,垂足为点O。
求证:四边形AEDF是菱形。
A
B
C
D
E
F
1
2
O
例题精讲
例4.已知:如图,□ABCD的对角线AC的垂直平分线与边AD、BC分别相交于点E、F。
求证:四边形AFCE是菱形。
C
F
B
A
E
D
O
例题精讲
有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可. 你知道其中的道理吗?
走进生活
能力提升
6.如图,在□ABCD中,E为BC上的一点,连接AE,BD,且AB=AE。
(1)求证:∠ABE=∠EAD。
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形。
A
B
C
D
E
3、判定定理2
对角线互相垂直的平行四边形是菱形.
1、定义法:
三、菱形的判定方法
2、判定定理1
有四条边相等的四边形是菱形.
或者说:对角线互相垂直平分的四边形是菱形.
回顾小结
成功就是99%的血汗,加上1%的灵感。
——爱迪生
再见!
第6章 平行四边形
6.3 特殊的平行四边形(4)
——菱形的判定定理
A
D
C
B
O
复习导入
1、什么叫做菱形?
2、菱形有哪些性质?
(1)边的关系:
(2)角的关系:
(3)对角线的关系:
(4)对称性:
我们又怎样来判断一个四边形
是菱形呢?
1、定义法:
一组邻边相等的平行四边形是菱形。
三、菱形的判定方法
A
B
C
D
几何语言
∵四边形ABCD是
平行四边形
AB=BC
∴四边形ABCD是菱形
A
B
C
D
探索(一)
已知:在四边形ABCD中,AB=BC
=CD=DA.
求证:四边形ABCD是菱形。
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
1、定义法:
三、菱形的判定方法
2、判定定理1
有四条边相等的四边形是菱形.
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
几何语言
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴ 平行四边形ABCD是菱形
探索(二)
已知:在平行四边形ABCD中,
AC ⊥ BD。
求证:平行四边形ABCD是菱形。
∴BO是AC的垂直平分线
3、判定定理2
对角线互相垂直的平行四边形是菱形.
1、定义法:
三、菱形的判定方法
2、判定定理1
有四条边相等的四边形是菱形.
A
B
C
D
O
∟
几何语言
∵在□ABCD中,
AC⊥BD
∴ □ABCD是菱形
或者说:对角线互相垂直平分的四边形是菱形.
例题精讲
例1.已知:如图,CE是△ABC的外角
∠ACD的平分线,AF∥CD交CE
于点F,FG∥AC交CD于点G.
求证:四边形ACGF是菱形。
A
B
C
D
E
F
G
1
2
3
4
例2、已知:AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F,求证:四边形AEDF是菱形。
例题精讲
A
B
C
D
E
F
1
2
3
4
例3、已知:AD是△ABC的角平分线,点E、F分别在边AB、AC上,且EF垂直平分AD,垂足为点O。
求证:四边形AEDF是菱形。
A
B
C
D
E
F
1
2
O
例题精讲
例4.已知:如图,□ABCD的对角线AC的垂直平分线与边AD、BC分别相交于点E、F。
求证:四边形AFCE是菱形。
C
F
B
A
E
D
O
例题精讲
有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可. 你知道其中的道理吗?
走进生活
能力提升
6.如图,在□ABCD中,E为BC上的一点,连接AE,BD,且AB=AE。
(1)求证:∠ABE=∠EAD。
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形。
A
B
C
D
E
3、判定定理2
对角线互相垂直的平行四边形是菱形.
1、定义法:
三、菱形的判定方法
2、判定定理1
有四条边相等的四边形是菱形.
或者说:对角线互相垂直平分的四边形是菱形.
回顾小结
成功就是99%的血汗,加上1%的灵感。
——爱迪生
再见!
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
