冀教版数学八年级下册22.2平行四边形的判定(一)课件(17张PPT)
文档属性
| 名称 | 冀教版数学八年级下册22.2平行四边形的判定(一)课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-02 18:20:55 | ||
图片预览




文档简介
(共17张PPT)
两组对边分别平行的四边形是平行四边形.
平行四边形的定义是什么?
复习回顾
几何语言
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形
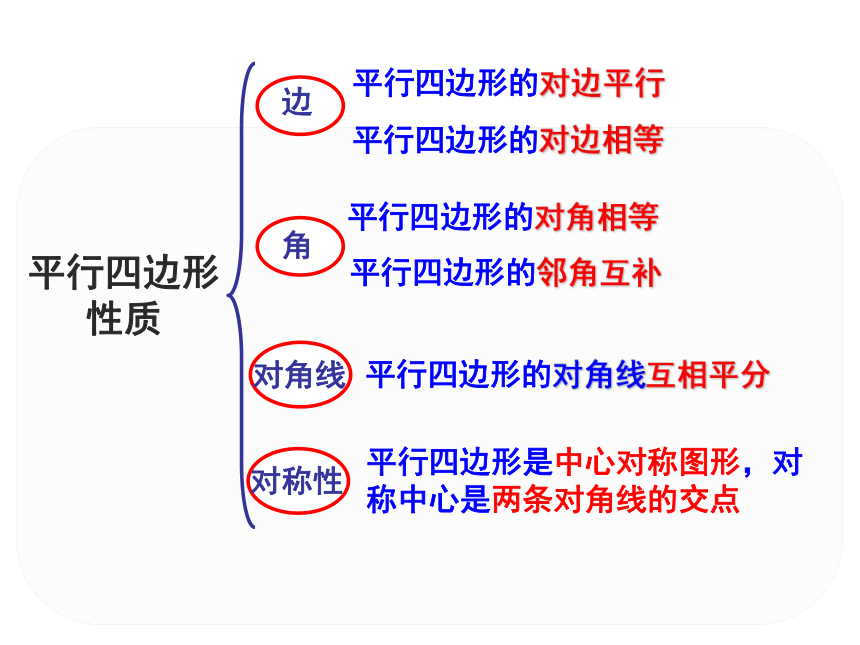
平行四边形 性质
平行四边形的对角线互相平分
平行四边形是中心对称图形,对称中心是两条对角线的交点
两组对边分别平行的四边形是平行四边形.
平行四边形的定义是什么?
温故知新
几何语言
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形
定义既是性质,也是判定.
条件(已知)
条件(已知)
结论(求证)
结论(求证)
22.2 平行四边形的判定(1)
1.掌握平行四边形的判定方法。
2.能根据不同条件灵活选取适当的平行四边形的 判定方法和性质进行推理、论证.
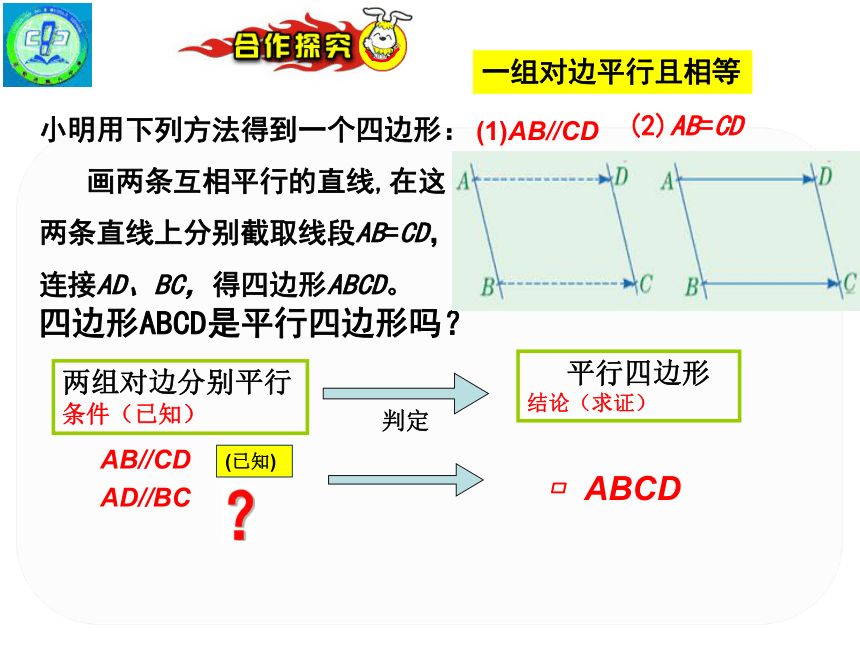
四边形ABCD是平行四边形吗?
小明用下列方法得到一个四边形:
画两条互相平行的直线,在这两条直线上分别截取线段AB=CD,连接AD、BC,得四边形ABCD。
两组对边分别平行 条件(已知)
平行四边形 结论(求证)
判定
AB//CD
AD//BC
?ABCD
(已知)
(1)AB//CD
(2)AB=CD
一组对边平行且相等
四边形问题转化三角形问题
由此发现:
一组对边平行且相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
几何语言:
∵ AD∥BC , AD=BC ,
∴ 四边形ABCD是平行四边形.
平行四边形的判定定理
A
B
C
D
条件(已知)
结论(求证)
已知:在四边形ABCD中,AB//CD,
请你再写出一个条件______,使得
四边形ABCD是平行四边形。
AB=CD
AD//BC
定理法:
一组对边平行且相等
的四边形是平行四边形.
小试牛刀
定义法:
两组对边分别平行
的四边形是平行四边形.
已知:如图所示,在?ABCD 中,E 为BA 延长线上一点,F 为DC 延长线上一点,且AE=CF,连接BF,DE.
求证四边形BFDE 是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵AE=CF,
∴BE=BA+AE=DC+CF=DF,且BE∥DF.
∴四边形BFDE是平行四边形.
例2 求证:平行线间的距离处处相等
已知:如图,EF∥MN,A,B为直线EF上任意两点,AD⊥MN,垂足为D,BC⊥MN,垂足为C.
求证AD=BC.
证明:∵AD⊥MN,BC⊥MN,
∴AD∥BC.
又∵EF∥MN,
∴四边形ADCB是平行四边形.
∴AD=BC.
证明线段相等方法:
平行四边形对边相等。
几何语言:
∵EF∥MN,
AD⊥MN,BC⊥MN,
∴AD=BC.
两组对角分别相等的四边形是平行四边形吗?
已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形。
两组对角分别相等的四边形是平行四边形.
几何语言:
∵ ∠A=∠C,∠B=∠D,
∴ 四边形ABCD是平行四边形.
平行四边形的判定定理
A
B
C
D
条件(已知)
结论(求证)
一、平行四边形的判定方法
1.两组对边分别_____的四边形是平行四边形.
2.一组对边_________的四边形是平行四边形.
3.两组对角分别_____的四边形是平行四边形.
二、平行线间的距离________.
两组对边分别平行的四边形是平行四边形.
平行四边形的定义是什么?
复习回顾
几何语言
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形
平行四边形 性质
平行四边形的对角线互相平分
平行四边形是中心对称图形,对称中心是两条对角线的交点
两组对边分别平行的四边形是平行四边形.
平行四边形的定义是什么?
温故知新
几何语言
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形
定义既是性质,也是判定.
条件(已知)
条件(已知)
结论(求证)
结论(求证)
22.2 平行四边形的判定(1)
1.掌握平行四边形的判定方法。
2.能根据不同条件灵活选取适当的平行四边形的 判定方法和性质进行推理、论证.
四边形ABCD是平行四边形吗?
小明用下列方法得到一个四边形:
画两条互相平行的直线,在这两条直线上分别截取线段AB=CD,连接AD、BC,得四边形ABCD。
两组对边分别平行 条件(已知)
平行四边形 结论(求证)
判定
AB//CD
AD//BC
?ABCD
(已知)
(1)AB//CD
(2)AB=CD
一组对边平行且相等
四边形问题转化三角形问题
由此发现:
一组对边平行且相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
几何语言:
∵ AD∥BC , AD=BC ,
∴ 四边形ABCD是平行四边形.
平行四边形的判定定理
A
B
C
D
条件(已知)
结论(求证)
已知:在四边形ABCD中,AB//CD,
请你再写出一个条件______,使得
四边形ABCD是平行四边形。
AB=CD
AD//BC
定理法:
一组对边平行且相等
的四边形是平行四边形.
小试牛刀
定义法:
两组对边分别平行
的四边形是平行四边形.
已知:如图所示,在?ABCD 中,E 为BA 延长线上一点,F 为DC 延长线上一点,且AE=CF,连接BF,DE.
求证四边形BFDE 是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵AE=CF,
∴BE=BA+AE=DC+CF=DF,且BE∥DF.
∴四边形BFDE是平行四边形.
例2 求证:平行线间的距离处处相等
已知:如图,EF∥MN,A,B为直线EF上任意两点,AD⊥MN,垂足为D,BC⊥MN,垂足为C.
求证AD=BC.
证明:∵AD⊥MN,BC⊥MN,
∴AD∥BC.
又∵EF∥MN,
∴四边形ADCB是平行四边形.
∴AD=BC.
证明线段相等方法:
平行四边形对边相等。
几何语言:
∵EF∥MN,
AD⊥MN,BC⊥MN,
∴AD=BC.
两组对角分别相等的四边形是平行四边形吗?
已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形。
两组对角分别相等的四边形是平行四边形.
几何语言:
∵ ∠A=∠C,∠B=∠D,
∴ 四边形ABCD是平行四边形.
平行四边形的判定定理
A
B
C
D
条件(已知)
结论(求证)
一、平行四边形的判定方法
1.两组对边分别_____的四边形是平行四边形.
2.一组对边_________的四边形是平行四边形.
3.两组对角分别_____的四边形是平行四边形.
二、平行线间的距离________.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
