沪教版数学八年级2019-2020学年度第二学期20.3一次函数的深度应用之二学案(含答案)
文档属性
| 名称 | 沪教版数学八年级2019-2020学年度第二学期20.3一次函数的深度应用之二学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 546.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-02 00:00:00 | ||
图片预览




文档简介
沪教版(上海)初中数学2019-2020学年度八年级数学同步教学案
一次函数的深度应用之二
【知识梳理】
根据实际问题建立一次函数解析式的方法:
(1)找等量关系;
(2)把已知的条件代入,变化的两个量用变量x,y来表示;
(3)求定义域:既要根据解析式又要根据实际意义求定义域.
【典型类型讲解】
题型一:文字应用
【例1】某商场计划投入一笔资金采购一批紧销商品,经过市场调查发现.如果月初售出,可获利15%,并可用本和利再投资其他商品,到月末又可获利10%;如果月末出售可获利30%.但要付出仓储费700元,请问根据商场的资金状况如何购销获利较多?
【分析】设商场投资x元,要比较两种获利的多少,关键是用x的关系式把两种获利方法表示出来.
【答案】设商场投资x元,在月初售出获利元,在月末售出获利元.
则,
.
(1)当时.,∴x=20 000.
(2)当时.x>20 000.
(3)当时,x<20 000.
即当商场投资两万元时,两种销售方式获利一样多.
当商场投资大于两万元时,第二种销售方式获利多.
当商场投资小于两万元时,第一种销售方式获利多.
【例2】某面粉厂有工人20名,为获取更多利润,增设加工面条项目,用本厂生产的面粉加工成面条(生产1千克面条需用面粉l千克).已知每人每天平均生产面粉600千克,或生产面条400千克.将面粉直接出售每千克可获利润0.2元,加工成面条后出售每干克面条可获利润0.6元,若每个工人一天只能做一项工作,且不计其他因素,设安排x名工人加工面条,
(1)求一天中加工面条所获利润为(元);
(2)求一天中剩余面粉所获利润为(元);
(3)当x为何值时,该厂一天中所获总利润y(元)最大?最大利润为多少元?
【分析】(1)由题意得.
(2)生产面粉的工人有()人,一天共生产面粉量为()600 kg.生产面条用去面粉400xkg,因此每天剩余面粉量应为600()-400x.售面粉获利;
(3)总利润=,注意题中隐含条件:400x≤600().
【答案】(l)..
(2).
(3)由题意,得.又因生产面条的千克数不超过生产面粉的千克数,即400x≤600(),解得x≤l2.因为y=40x+2 400中y随着x的增大而增大.所以当x=12时,总利润y最大,此时y=40×12+2 400=2 880(元).
【借题发挥】
1. 某工程队要招聘甲、乙两种工种的工人150人,甲、乙两种工种的工人的月资分为600元和1000元,现要求乙种工种的人数不少于甲种丁种的人数的2倍,问甲、乙两种工种各招聘多少人时,使每月所付的工资最少?
【答案】设招聘甲种工种的工人为x人,则招聘乙种工种的工人为人.
由题意,得,解得x≤50,
∴0≤x≤50.设所聘请的工人共需付月工资为y元.
则.
∵,∴y随x的增大而减小,∴当时,
y有最小值,最小值为(元).
.
故要使每月所付工资最少,应招聘甲种工人50人,乙种工人100人,这时所付月工资总额为130 000元.
2. 我市某中学要印制本校高中招生的录取通知书,有两个印刷厂前来联系制作业务,甲厂的优惠条件是:按每份定价1.5元的八折收费,另收900元制版费;乙厂的优惠条件是:每份定价1.5元价格不变,而制版费900元则六折优惠,且甲、乙两厂都规定:一次印刷数量至少是500份.
(1)分别求两个印刷厂的收费y(元)与印刷数量x(份)的函数关系式,并指出自变量x的取值范围;
(2)如何根据印刷的数量选择比较合算的方案?如果这个中学要印制2 000份录取通知书,那么应当选择哪一个厂?需要多少费用?
【答案】(l) (x≥500.且x为整数).
(x≥500,且x为整数).
(2)解法一:若,则,所以x<1 200;
若,则.所以x=1 200;
若,则.所以x>1 200;
因为2 000>1 200.所以=1.2×2 000+900=3 300.
综上所述,
当500≤x<1 200份时,选择乙厂比较合算;
当x=1 200份时,两工厂的费用相同;
当x>1 200份时,选择甲厂比较合算.
所以要印制2 000份录取通知书,应选择甲厂,费用是3 300元.
题型二:数形结合
【例3】某地区一种商品的需求量(万件)、供应量(万件)与价格x(元/件)分别近似满足下列函数关系式:.如图20-4-5所示,需求量为0时,即停止供应.当时,该商品的价格称为稳定价格,需求量称为稳定需求量.
(1)求该商品的稳定价格与稳定需求量;
(2)价格在什么范围,该商品的需求量低于供应量?
(3)当需求量高于供应量时,政府常通过对供应方提供价格补贴来提高供货价格,以提高供应量,现若要使稳定需求量增加4万件,政府应对每件商品提供多少元补贴,才能使供应量等于需求量?
【分析】(1)主要考查对稳定价格、稳定需求量的理解.由求出x即为稳定价格,把x代入或即为稳定需求量;(2)由图13-3-12知,当32
解这个方程,得x=32.此时.
所以,该商品的稳定价格为32元/件,稳定需求量为28万件.
(2)因为“需求量为0时,即停止供应”,所以,当时,有x=60.
又由图像,知x>32.
所以,当价格大于32元/件而小于60元/件时,该商品的需求量低于供应量.
(3)设政府部门对该商品每件应提供元补贴.根据题意,得
解得
所以,政府部门对该商品每件应提供6元的补贴.
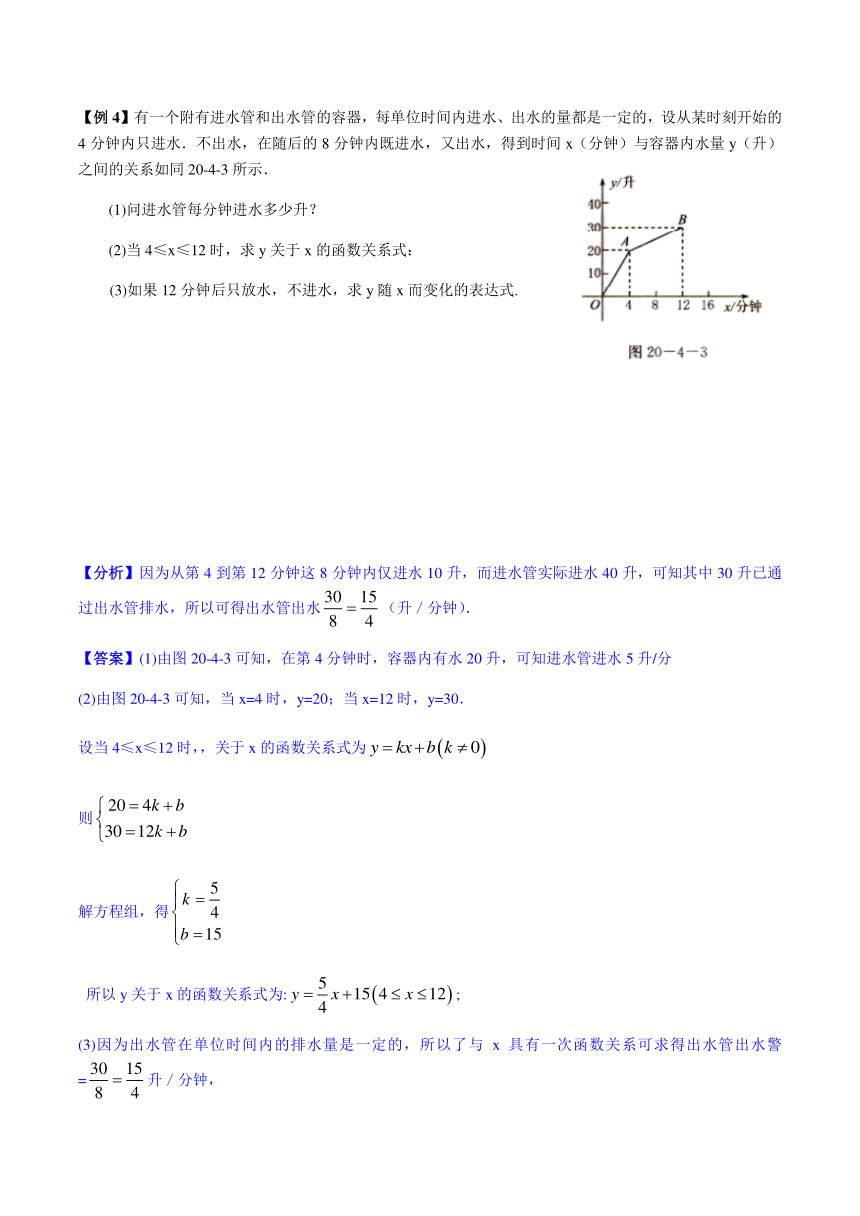
【例4】有一个附有进水管和出水管的容器,每单位时间内进水、出水的量都是一定的,设从某时刻开始的4分钟内只进水.不出水,在随后的8分钟内既进水,又出水,得到时间x(分钟)与容器内水量y(升)之间的关系如同20-4-3所示.
(1)问进水管每分钟进水多少升?
(2)当4≤x≤12时,求y关于x的函数关系式:
(3)如果12分钟后只放水,不进水,求y随x而变化的表达式.
【分析】因为从第4到第12分钟这8分钟内仅进水10升,而进水管实际进水40升,可知其中30升已通过出水管排水,所以可得出水管出水(升/分钟).
【答案】(1)由图20-4-3可知,在第4分钟时,容器内有水20升,可知进水管进水5升/分
(2)由图20-4-3可知,当x=4时,y=20;当x=12时,y=30.
设当4≤x≤12时,,关于x的函数关系式为
则
解方程组,得
所以y关于x的函数关系式为:;
(3)因为出水管在单位时间内的排水量是一定的,所以了与x具有一次函数关系可求得出水管出水警=升/分钟,
设当x≥12时,y关于x的函数关系式为:.
由图20-4-3可知,当x=12时,y= 30.则:.
解方程,得.
因为30升水需分钟排完,所以y关于x的函数关系式为
(12≤x≤20).
【借题发挥】
1. 某图书馆开设两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡.使用这两种方式租书,租书金额y(元)与租书时间x(天)之间的关系如图20-4-4所示,根据图中的信息回答下列问题:
(1)写出两种方式的租书金额y(元)与租书时间x(天)之间的函数关系式;
(2)求出两种租书方式下每天的收费分别是多少元;
(3)若两种卡的使用期限均为一年,则在这一年中如何选取这两种租书方式比较划算?
【答案】(1)设使用租书卡的金额(元)与时间x(天)的函数关系式为,
由图像可知:直线经过(100,50).
所以,所以,即.
设使用会员卡的金额(元)与时间x(天)的函数关系式为.由图像可知:直线经过(0,20),(100,50).
所以,解得所以.
(2)由于使用租书卡每I00天收费50元,所以50÷l00=0.5(元/天);由于使用会员卡每100天收费元,所以30÷100=0.3(元/天).
(3)由图像可知:当x=100时,;当x>100时,在的上方,即;
当x<100时,在的下方,即.
故当时间为100天时,用两种卡一样划算;当时间在100天以内时,用租书卡划算;当时间在100天到一年时,用会员卡划算.
【随堂练习】
1.某人以60 km/h的速度驾驶汽车从A地出发,那么他行驶的距离y( km)和行驶的时间x(h)的函数关系式为_______________________.
2.小王带了5元去购买铅笔,铅笔每支售价0.22元,那么小王剩余的钱款数y(元)关于购买铅笔支数x的函数解析式是____________________.
3.一根蜡烛长20 cm,点燃后每一小时燃烧5 cm,燃烧时剩下的高度 (cm)与燃烧时间t(小时)的函数关系式是__________________.
4.一水库蓄水,从开闸放水起,每小时放水那么水库蓄水量y()关于开闸时间t(时)的函数解析式是____________________.
5.如图,直角三角形ABC中,,BD是角平分线,且,那么y关于x的函数关系式是______________________.
【答案】
1.;
2.(x是整数,且);
3.;
4.;
5..
6.声音在空气中传播速度y( m/s)是气温x(℃)的一次函数,下表列出了一组不同气温时的音速:
气温x(℃) 0 5 10 15 20
音速y(m/s) 331 334 337 340 343
(1)求y与x之间的函数关系式;
(2)当气温为22℃时,某人看到烟花燃放5s后才听到声响,那么此人与燃放烟花所在地约相距多远?
【答案】(1);(2)1721米.
7.某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5
米的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1米污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元.
(1)求出y与x的函数关系式;(纯利润=总收入一总支出)
(2)当y=106000时,求该厂在这个月中生产产品的件数.
【答案】(1);(2)6000件.
8.为了保护学生的视力,课桌椅的高度都是按一定的关系配套设计的,研究表明;假设
椅子的高度(不含靠背)为x( cm),课桌的高度为y( cm),则y应是x的一次函数,下
表列出两套符合条件的课桌椅的高度:
第一套 第二套
椅子高度x(cm) 41 44
桌子高度y(cm) 75 81
(1)试确定y与x之间的函数关系式;
(2)现有一把高42.0cm的椅子和一张高78. 2cm的课桌,它们是否配套?请通过计算说明理由.为什么?
【答案】(1);(2)当时,,所以不配套.
9.某企业有甲、乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图像如图所示,结合图像回答下列问题:
(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式;
(2)求注水多长时间甲、乙两个蓄水池水的深度相同;
(3)求注水多长时间甲、乙两个蓄水池的蓄水量相同.
【答案】(1);
(2)当小时两池水深相等;
(3)当3小时时甲池水全部进入乙池,此时两池的水都在乙池,它的深度为4米,因此当两池水相等时,实际上乙池的水深为2米,所以.
【课堂总结】
【课后作业】
一、基础复习巩固
填空题:
1.已知一次函数.则k=________________.
2.直线与直线相交于y轴,且与直线平行,则直线的解析式为____________________.
3.对于一次函数,当x=___________时,图像在x轴下方.
4.一次函数的图像与坐标轴所围成的三角形面积是______________.
5.已知一次函数的图像不经过第二象限,则正比例函数必定经过第__________象限.
6.若直线和直线的交点坐标为(m,8),则____________.
7.某单位为鼓励职工节约用水,作出了以下规定:每位职工每月用水不超过10立方米的,按每立方米m元水费收费;用水超过10立方米的,超过部分加倍收费.某职工某月缴水费16m元,则该职工这个月实际用水为_______________立方米.
【答案】
1. ;
2.;
3.;
4.4;
5.一,三;
6.16;
7.13.
选择题:
8.下列函数中,y随x的增大而减小的有 ( )
①②⑧④
A. 1个 B.2个 C.3个 I).4个
9.已知一次函数的图像如图所示,则 ( )
A.k>0,b>0
B.k<0,b<0
C.k>0,b<0
D.k<0,b>0
10.弹簧的长度ycm与所挂物体的质量x(kg)的关系是一次函数,图像如图所示,则弹簧不挂物体时的长度是 ( )
A. 9cm B.l0cm C.10.5cm D. 11cm
11.如图,OA,BA分别表示甲、乙两名学生运动的一次函数图像,图中s和t分别表示运动路程和时间,根据图像判断快者的速度比慢者的速度每秒快 ( )
A.2.5米 B.2米 C.1.5米 D. 1米
12.已知函数,当一1
A. B. C. D.
【答案】D;D;B;C;C;A.
14.某移动公司为用户提供两种资费方式拨打市话.甲:拨打和接听市话0. 40元/min,但
每月要交50元月租费;乙:拨打和接听市话0.60元/min,不收月租费.
(l)分别写出两种资费方式下的费用y(元)与拨打或接听电话时间t(min)之间的关系式:
(2)在同一直角坐标系中画出它们的图像;
(3)若某人每月需使用手机通话200min,选择哪种付费方式能合算一些?若某人计划每月花费160元手机话费,选择哪种付费方式能多使用一些时间?
【答案】(1);(2)略;(3)当时,,因此选择乙;当时,元,因此选择甲.
15.某家电集团公司生产某种型号的新家电,前期投资200万元,每生产1台这种新家电后期还需其他投资0.3万元,已知每台新家电可实现产值0.5万元.
(1)分别求总投资(万元)和总利润(万元)关于新家电的总产量x(台)的函数关系式;
(2)当新家电的总产量为900台时,该公司的盈利情况如何?
(3)请你利用第一小题中与x的函数关系式分析该公司的盈亏情况.
(注:总投资=前期投资+后期投资。总利润=总产值一总投资)
【答案】(1);
(2)当时,,因此亏损20万元;
(3)当时盈利,当时持平,当时亏损.
16.某空军加油飞机接到命令,立即给另一架正在飞行的运输机进行空中加油,在加油过程中,设运输飞机的油箱余油量为吨,加油飞机的加油箱余油量为吨,加油时间为t(分), 、与t之间的函数图像如图所示,结合图像回答下列问题:
(1)加油飞机的加油油箱中装载了_______________吨油;将这些油全部加给运输飞机需___________钟;
(2)求加油过程中,运输飞机的余油量(吨)与时间t(分)的函数关系式;
(3)运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用?说明理由
【答案】(1)30吨,10分钟;(2);(3)运输机每小时的耗油量为(吨),因此10小时的耗油量为(吨)<69吨,因此够用.
17.教室里放有一台饮水机,饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的,两个放水管同时打开
时,他们的流量相同,放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:
(1)求出饮水机的存水量y(升)与放水时间x(分钟)(x≥2)的函数关系式;
(2)如果打开第一个水管后,2分钟时恰好有4个同学接水结束,则前22个同学接水结束共需要几分钟?
(3)按(2)的放法,求出在课间10分钟内班级中最多有多少个同学能及时接完水?
【答案】(1);
(2)当时,
(3)时,人.
