人教版(2019版)高一物理必修二第七章第3节万有引力的成就 (共38页)
文档属性
| 名称 | 人教版(2019版)高一物理必修二第七章第3节万有引力的成就 (共38页) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-02 17:48:00 | ||
图片预览











文档简介
(共38张PPT)
第3节 万有引力理论的成就
学习目标定位
1.掌握应用万有引力定律解决问题的基本思路
3.会根据条件计算天体的密度
2.掌握两种计算天体质量的方法
4.了解发现未知天体的基本思路
目录
一、“称量”地球的质量
二、计算天体的质量
三、发现未知天体
四、预言哈雷彗星回归
1、万有引力定律的内容是什么?
2、该定律的适用条件是什么?
3、比例系数G是怎样测量的?
复习回顾
关于万有引力的说明:
(1)普遍性:它是自然界中物质之间的基本的相互作用之一,存在于任何客观存在的两部分有质量之间。
(2)相互性:两个物体相互作用的引力是一对作用力与反作用力。
(3)宏观性:通常情况下,它非常小。只有在质量巨大的天体间,它的存在才有宏观物理意义。
复习回顾
思考: 根据所学的知识你能解释为什么可以不考虑地球自转的影响呢?
结论:向心力远小于重力,万有引力大小近似等于重力。因此一般粗略计算中不考虑(或忽略)地球自转的影响。
R
M
θ
ω
r
m
mg
F向
F引
试求:
质量为1kg的物体静止在赤道上时的向心加速度。(已知地球半径R=6.×106m)
答案:a=0.034m/s2
复习回顾
重力加速度 g 的变化
1)重力是万有引力的分力
万有引力
自转向心力
重 力
3)重力加速度g的大小
在地表球面时
离地面h高处
在赤道时重力最小、两极时最大且等于万有引力。
2)重力加速度g的变化
随纬度增大而增大,随高度增大而减小
R
M
θ
ω
r
m
mg
F向
F引
一、“称量”地球的质量
阿基米德:“给我一个支点,我可以撬动地球”
那是否我们给他一个天平(杠杆)他就能测量地球的质量了呢?
No,地球的质量无法用天平测量
高中物理
问题一:
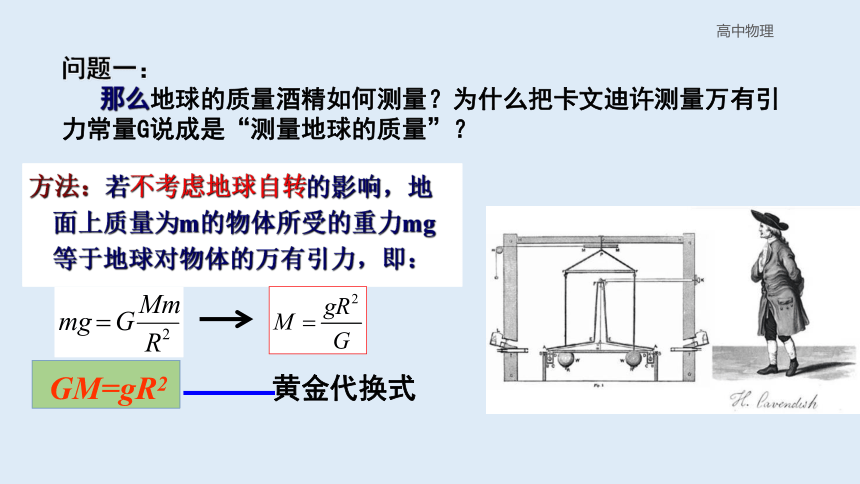
那么地球的质量酒精如何测量?为什么把卡文迪许测量万有引力常量G说成是“测量地球的质量”?
方法:若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的万有引力,即:
GM=gR2
黄金代换式
例1:设地面附近的重力加速度g=9.8 m/s2,地球半径R=6.4×106 m,引力常量G=6.67×10-11 N·m2/kg2,试估算地球的质量.
答案 ME=
忽略地球自转
应用万有引力可算出地球的质量,能否算出其他天体的质量呢?
二、计算天体的质量
方法1、选定一颗绕地球转动的卫星(例如月球),测定卫星的轨道半径和周期。
方法2、若已知卫星绕地球做匀速圆周运动的的半径r和运行的线速度v。
问题二:
你还有其他办法测量出地球的质量吗?需要测量那些物理量呢?
中心天体M
环绕天体m
明确各个物理量
轨道半径r
地球
月球
r是地月轨道半径,T是月球的公转周期
中心天体的半径R
应用万有引力计算天体质量的基本思路:
1.确定中心天体,找出绕该天体作匀速圆周运动的物体;
2.建立天体运动的基本方程;
F万=F向
3.明确方程中各物理量的涵义。
总结
需要条件:线速度v;轨道半径r。
需要条件:角速度ω;轨道半径r
需要条件:公转周期T;轨道半径r
上面三式中,因为线速度与角速度实际操作中不好测量,周期好测量,所以我们用得最多的公式将会是第三个
例2、回答下面3个小问题。
①如果以水星绕太阳做匀速圆周运动为研究对象,需要知道哪些量才能求得太阳的质量?
需要知道水星做匀速圆周运动的公转周期T及公转半径 r
②水星和地球绕太阳做圆周运动的公转周 期T是不一样的,公转半径也是不一样的, 那用公式 求解出来的太阳的质量会是一样的吗?
是一样的,根据开普勒第三定律,对于同一中心天体,所有环绕天体
的值是
有
一样的。所以
③你现在能证明开普勒第三定律
中的k与中心天体有关吗?
1.天体质量及半径求出后,如何得到天体的平均密度?
答案 ρ=
求出天体体积
2.(1)由天体表面的重力加速度g和半径R,求此天体的密度.
(2)若天体的某个行星(或卫星)的轨道半径为r,运行周期为T,中心天体的半径为R,
由mg= 和M=ρ· πR3,得ρ=
由 和M=ρ· πR3,得ρ=
注意 R、r的意义不同,一般地R指中心天体的半径,r指行星或卫星的轨道半径,若绕近地轨道运行,则有R=r,此时ρ
= .
天体密度的计算方法
不同星球表面的力学规律相同,只是重力加速度g不同,在解决其他星球表面上的力学问题时,若要用到重力加速度应该是该星球的重力加速度,如:竖直上抛运动、平抛运动、竖直平面内的圆周运动,都要用该星球的重力加速度。
三、发现未知天体
预见并发现未知行星,是万有引力理论威力和价值的最生动例证.
在1781年发现的第七个行星—天王星的运动轨道,总是同根据万有引力定律计算出来的有一定偏离.当时有人预测,肯定在其轨道外还有一颗未发现的新星,这就是后来发现的第八大行星—海王星.人们称其为“笔尖下发现的行星” 。
海王星
英国的亚当斯和法国的勒维耶
英国剑桥大学的学生,23岁的亚当斯,他根据万有引力定律和天王星的真实轨道逆推,预言了新行星不同时刻所在的位置。同年,法国的勒维列也算出了同样的结果,并把预言的结果寄给了柏林天文学家加勒。当晚(1846.3.14),加勒把望远镜对准勒维列预言的位置,果然发现有一颗新的行星——就是海王星.
海王星发现之后,人们发现它的轨道也与理论计算的不一致。于是几位学者用亚当斯和勒维耶的方法预言另一颗新行星的存在.
在预言提出之后,1930年,汤博发现了太阳系的后来曾被称为第九大行星的冥王星
冥王星和它的卫星
美国宇航局(NASA)提供的冥王星(上者)与它的卫星的画面
九大行星成为了过去史
冥王星
? 国际天文学联合会大会24日投票决定,不再将传统九大行星之一的冥王星视为行星,而将其列入“矮行星”。许多人感到不解,为什么从儿时起就一直熟知的太阳系“九大行星”概念如今要被重新定义,而冥王星又因何被“降级”?
????“行星”这个说法起源于希腊语,原意指太阳系中的“漫游者”。近千年来,人们一直认为水星、金星、地球、火星、木星和土星是太阳系中的标准行星。19世纪后,天文学家陆续发现了天王星、海王星和冥王星,使太阳系的“行星”变成了9颗。此后,“九大行星”成为家喻户晓的说法。
???? 不过,新的天文发现不断使“九大行星”的传统观念受到质疑。天文学家先后发现冥王星与太阳系其他行星的一些不同之处。冥王星所处的轨道在海王星之外,属于太阳系外围的柯伊伯带,这个区域一直是太阳系小行星和彗星诞生的地方。20世纪90年代以来,天文学家发现柯伊伯带有更多围绕太阳运行的大天体。比如,美国天文学家布朗发现的“2003UB313”,就是一个直径和质量都超过冥王星的天体。
??? ?布朗等人的发现使传统行星定义遭遇巨大挑战。国际天文学联合会大会通过的新行星定义,意在弥合传统的行星概念与新发现的差距。
???? 大会通过的决议规定,“行星”指的是围绕太阳运转、自身引力足以克服其刚体力而使天体呈圆球状、能够清除其轨道附近其他物体的天体。在太阳系传统的“九大行星”中,只有水星、金星、地球、火星、木星、土星、天王星和海王星符合这些要求。冥王星由于其轨道与海王星的轨道相交,不符合新的行星定义,因此被自动降级为“矮行星”。
冥王星为什么会被“降级”?
差点KO人类的2019OK小行星,有办法KO它吗?
我们又将如何自救?
https://haokan.baidu.com/v?vid=12352988852599553818&pd=bjh&fr=bjhauthor&type=video
四、预言哈雷彗星回归
在牛顿之前,彗星被看作是一种神秘的现象。英国天文学家哈雷从1337年到1698年的慧星记录中挑选了24颗彗星,依据万有引力定律,用一年时间计算了它们的轨道发现1531年、1607年和1682年出现的这三颗粘星轨道看起来如出一辙,他大胆预言,这三次出现的梦星是同一颗星,周期约为76年,并预言它将于1758年底或1759年初再次回归。1759年3月这颗彎星如期通过了近日点,它最近一次回归是1986年,它的下次回归将在2061年左右。
海王星的发现和哈雷售星的“按时回归”确立了万有引力定律的地位,也成为科学史上的美谈诺贝尔奖获得者物理学家劳厄说:“没有任何东西像牛顿引力理论对行星轨道的计算那样,如此有力地树立起人们对年轻的物理学的尊敬。从此以后,这门自然科学成了巨大的精神工国……”牛顿还用月球和太阳的万有引力解释了潮汐现象、用万有引力定律和其他力学定律,推测地球呈赤道处略为隆起的扁平形状。万有引力定律可以用于分析地球表面重力加速度微小差异的原因,以及指导重力探矿除了上述成就外,万有引力定律的另重要应用将在下节讲述。
你的名字
一、天体质量和密度的计算
典例精析
例1 地球表面的平均重力加速度为g,地球半径为R,引力常量为G,可估算地球的平均密度为( )
A
A. B.
C. D.
例2 假设在半径为R的某天体上发射一颗该天体的卫星.若它贴近该天体的表面做匀速圆周运动的周期为T1,已知万有引力常量为G.
(1)则该天体的密度是多少?
(2)若这颗卫星距该天体表面的高度为h,测得在该处做圆周运动的周期为T2,则该天体的密度又是多少?
典例精析
一、天体质量和密度的计算
(1)设卫星质量为m,天体质量
为M,卫星贴近天体表面运动时
天体的体积为:
故该天体的密度为
例2 假设在半径为R的某天体上发射一颗该天体的卫星.若它贴近该天体的表面做匀速圆周运动的周期为T1,已知万有引力常量为G.
(1)则该天体的密度是多少?
(2)若这颗卫星距该天体表面的高度为h,测得在该处做圆周运动的周期为T2,则该天体的密度又是多少?
典例精析
一、天体质量和密度的计算
(2)卫星距天体表面为h时,忽
略自转有
本课小结
(当卫星在天体表面做近地飞行呢?)
(1)某星体m围绕中心天体M做圆周运动的周期为T,半径为r
(3)中心天体密度
(2)已知中心天体的半径R和表面g
GM=gR2
黄金代换式
万有引力定律的应用
测天体的质量、密度
行星、卫星的运动
宇宙速度
同步卫星
思路一:天体表面重力近似等于万有引力
思路二:天体运动中,万有引力提供物体圆周运动向心力
重力加速度g
自我检测区
1
2
3
1.(天体质量的计算)“嫦娥三号”探月卫星于2013年12月2日凌晨在西昌卫星发射中心发射,实现了“落月”的新阶段.若已知引力常量为G,月球绕地球做圆周运动的半径为r1、周期为T1,“嫦娥三号”探月卫星做圆周运动的环月轨道半径为r2、周期为T2,不计其他天体的影响,根据题目条件可以( )
A.求出“嫦娥三号”探月卫星的质量
B.求出月球的质量
C.得出
D.求出地球的密度
1
2
3
两个模型:
月
月
可求中心天体质量
同
理
周期定律表达形式
条件:中心天体相同
1.(天体质量的计算)“嫦娥三号”探月卫星于2013年12月2日凌晨在西昌卫星发射中心发射,实现了“落月”的新阶段.若已知引力常量为G,月球绕地球做圆周运动的半径为r1、周期为T1,“嫦娥三号”探月卫星做圆周运动的环月轨道半径为r2、周期为T2,不计其他天体的影响,根据题目条件可以( )
A.求出“嫦娥三号”探月卫星的质量
B.求出月球的质量
C.得出
D.求出地球的密度
两个模型:
B
月
可求中心天体质量
周期定律表达形式
条件:中心天体相同
1
2
3
第3节 万有引力理论的成就
学习目标定位
1.掌握应用万有引力定律解决问题的基本思路
3.会根据条件计算天体的密度
2.掌握两种计算天体质量的方法
4.了解发现未知天体的基本思路
目录
一、“称量”地球的质量
二、计算天体的质量
三、发现未知天体
四、预言哈雷彗星回归
1、万有引力定律的内容是什么?
2、该定律的适用条件是什么?
3、比例系数G是怎样测量的?
复习回顾
关于万有引力的说明:
(1)普遍性:它是自然界中物质之间的基本的相互作用之一,存在于任何客观存在的两部分有质量之间。
(2)相互性:两个物体相互作用的引力是一对作用力与反作用力。
(3)宏观性:通常情况下,它非常小。只有在质量巨大的天体间,它的存在才有宏观物理意义。
复习回顾
思考: 根据所学的知识你能解释为什么可以不考虑地球自转的影响呢?
结论:向心力远小于重力,万有引力大小近似等于重力。因此一般粗略计算中不考虑(或忽略)地球自转的影响。
R
M
θ
ω
r
m
mg
F向
F引
试求:
质量为1kg的物体静止在赤道上时的向心加速度。(已知地球半径R=6.×106m)
答案:a=0.034m/s2
复习回顾
重力加速度 g 的变化
1)重力是万有引力的分力
万有引力
自转向心力
重 力
3)重力加速度g的大小
在地表球面时
离地面h高处
在赤道时重力最小、两极时最大且等于万有引力。
2)重力加速度g的变化
随纬度增大而增大,随高度增大而减小
R
M
θ
ω
r
m
mg
F向
F引
一、“称量”地球的质量
阿基米德:“给我一个支点,我可以撬动地球”
那是否我们给他一个天平(杠杆)他就能测量地球的质量了呢?
No,地球的质量无法用天平测量
高中物理
问题一:
那么地球的质量酒精如何测量?为什么把卡文迪许测量万有引力常量G说成是“测量地球的质量”?
方法:若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的万有引力,即:
GM=gR2
黄金代换式
例1:设地面附近的重力加速度g=9.8 m/s2,地球半径R=6.4×106 m,引力常量G=6.67×10-11 N·m2/kg2,试估算地球的质量.
答案 ME=
忽略地球自转
应用万有引力可算出地球的质量,能否算出其他天体的质量呢?
二、计算天体的质量
方法1、选定一颗绕地球转动的卫星(例如月球),测定卫星的轨道半径和周期。
方法2、若已知卫星绕地球做匀速圆周运动的的半径r和运行的线速度v。
问题二:
你还有其他办法测量出地球的质量吗?需要测量那些物理量呢?
中心天体M
环绕天体m
明确各个物理量
轨道半径r
地球
月球
r是地月轨道半径,T是月球的公转周期
中心天体的半径R
应用万有引力计算天体质量的基本思路:
1.确定中心天体,找出绕该天体作匀速圆周运动的物体;
2.建立天体运动的基本方程;
F万=F向
3.明确方程中各物理量的涵义。
总结
需要条件:线速度v;轨道半径r。
需要条件:角速度ω;轨道半径r
需要条件:公转周期T;轨道半径r
上面三式中,因为线速度与角速度实际操作中不好测量,周期好测量,所以我们用得最多的公式将会是第三个
例2、回答下面3个小问题。
①如果以水星绕太阳做匀速圆周运动为研究对象,需要知道哪些量才能求得太阳的质量?
需要知道水星做匀速圆周运动的公转周期T及公转半径 r
②水星和地球绕太阳做圆周运动的公转周 期T是不一样的,公转半径也是不一样的, 那用公式 求解出来的太阳的质量会是一样的吗?
是一样的,根据开普勒第三定律,对于同一中心天体,所有环绕天体
的值是
有
一样的。所以
③你现在能证明开普勒第三定律
中的k与中心天体有关吗?
1.天体质量及半径求出后,如何得到天体的平均密度?
答案 ρ=
求出天体体积
2.(1)由天体表面的重力加速度g和半径R,求此天体的密度.
(2)若天体的某个行星(或卫星)的轨道半径为r,运行周期为T,中心天体的半径为R,
由mg= 和M=ρ· πR3,得ρ=
由 和M=ρ· πR3,得ρ=
注意 R、r的意义不同,一般地R指中心天体的半径,r指行星或卫星的轨道半径,若绕近地轨道运行,则有R=r,此时ρ
= .
天体密度的计算方法
不同星球表面的力学规律相同,只是重力加速度g不同,在解决其他星球表面上的力学问题时,若要用到重力加速度应该是该星球的重力加速度,如:竖直上抛运动、平抛运动、竖直平面内的圆周运动,都要用该星球的重力加速度。
三、发现未知天体
预见并发现未知行星,是万有引力理论威力和价值的最生动例证.
在1781年发现的第七个行星—天王星的运动轨道,总是同根据万有引力定律计算出来的有一定偏离.当时有人预测,肯定在其轨道外还有一颗未发现的新星,这就是后来发现的第八大行星—海王星.人们称其为“笔尖下发现的行星” 。
海王星
英国的亚当斯和法国的勒维耶
英国剑桥大学的学生,23岁的亚当斯,他根据万有引力定律和天王星的真实轨道逆推,预言了新行星不同时刻所在的位置。同年,法国的勒维列也算出了同样的结果,并把预言的结果寄给了柏林天文学家加勒。当晚(1846.3.14),加勒把望远镜对准勒维列预言的位置,果然发现有一颗新的行星——就是海王星.
海王星发现之后,人们发现它的轨道也与理论计算的不一致。于是几位学者用亚当斯和勒维耶的方法预言另一颗新行星的存在.
在预言提出之后,1930年,汤博发现了太阳系的后来曾被称为第九大行星的冥王星
冥王星和它的卫星
美国宇航局(NASA)提供的冥王星(上者)与它的卫星的画面
九大行星成为了过去史
冥王星
? 国际天文学联合会大会24日投票决定,不再将传统九大行星之一的冥王星视为行星,而将其列入“矮行星”。许多人感到不解,为什么从儿时起就一直熟知的太阳系“九大行星”概念如今要被重新定义,而冥王星又因何被“降级”?
????“行星”这个说法起源于希腊语,原意指太阳系中的“漫游者”。近千年来,人们一直认为水星、金星、地球、火星、木星和土星是太阳系中的标准行星。19世纪后,天文学家陆续发现了天王星、海王星和冥王星,使太阳系的“行星”变成了9颗。此后,“九大行星”成为家喻户晓的说法。
???? 不过,新的天文发现不断使“九大行星”的传统观念受到质疑。天文学家先后发现冥王星与太阳系其他行星的一些不同之处。冥王星所处的轨道在海王星之外,属于太阳系外围的柯伊伯带,这个区域一直是太阳系小行星和彗星诞生的地方。20世纪90年代以来,天文学家发现柯伊伯带有更多围绕太阳运行的大天体。比如,美国天文学家布朗发现的“2003UB313”,就是一个直径和质量都超过冥王星的天体。
??? ?布朗等人的发现使传统行星定义遭遇巨大挑战。国际天文学联合会大会通过的新行星定义,意在弥合传统的行星概念与新发现的差距。
???? 大会通过的决议规定,“行星”指的是围绕太阳运转、自身引力足以克服其刚体力而使天体呈圆球状、能够清除其轨道附近其他物体的天体。在太阳系传统的“九大行星”中,只有水星、金星、地球、火星、木星、土星、天王星和海王星符合这些要求。冥王星由于其轨道与海王星的轨道相交,不符合新的行星定义,因此被自动降级为“矮行星”。
冥王星为什么会被“降级”?
差点KO人类的2019OK小行星,有办法KO它吗?
我们又将如何自救?
https://haokan.baidu.com/v?vid=12352988852599553818&pd=bjh&fr=bjhauthor&type=video
四、预言哈雷彗星回归
在牛顿之前,彗星被看作是一种神秘的现象。英国天文学家哈雷从1337年到1698年的慧星记录中挑选了24颗彗星,依据万有引力定律,用一年时间计算了它们的轨道发现1531年、1607年和1682年出现的这三颗粘星轨道看起来如出一辙,他大胆预言,这三次出现的梦星是同一颗星,周期约为76年,并预言它将于1758年底或1759年初再次回归。1759年3月这颗彎星如期通过了近日点,它最近一次回归是1986年,它的下次回归将在2061年左右。
海王星的发现和哈雷售星的“按时回归”确立了万有引力定律的地位,也成为科学史上的美谈诺贝尔奖获得者物理学家劳厄说:“没有任何东西像牛顿引力理论对行星轨道的计算那样,如此有力地树立起人们对年轻的物理学的尊敬。从此以后,这门自然科学成了巨大的精神工国……”牛顿还用月球和太阳的万有引力解释了潮汐现象、用万有引力定律和其他力学定律,推测地球呈赤道处略为隆起的扁平形状。万有引力定律可以用于分析地球表面重力加速度微小差异的原因,以及指导重力探矿除了上述成就外,万有引力定律的另重要应用将在下节讲述。
你的名字
一、天体质量和密度的计算
典例精析
例1 地球表面的平均重力加速度为g,地球半径为R,引力常量为G,可估算地球的平均密度为( )
A
A. B.
C. D.
例2 假设在半径为R的某天体上发射一颗该天体的卫星.若它贴近该天体的表面做匀速圆周运动的周期为T1,已知万有引力常量为G.
(1)则该天体的密度是多少?
(2)若这颗卫星距该天体表面的高度为h,测得在该处做圆周运动的周期为T2,则该天体的密度又是多少?
典例精析
一、天体质量和密度的计算
(1)设卫星质量为m,天体质量
为M,卫星贴近天体表面运动时
天体的体积为:
故该天体的密度为
例2 假设在半径为R的某天体上发射一颗该天体的卫星.若它贴近该天体的表面做匀速圆周运动的周期为T1,已知万有引力常量为G.
(1)则该天体的密度是多少?
(2)若这颗卫星距该天体表面的高度为h,测得在该处做圆周运动的周期为T2,则该天体的密度又是多少?
典例精析
一、天体质量和密度的计算
(2)卫星距天体表面为h时,忽
略自转有
本课小结
(当卫星在天体表面做近地飞行呢?)
(1)某星体m围绕中心天体M做圆周运动的周期为T,半径为r
(3)中心天体密度
(2)已知中心天体的半径R和表面g
GM=gR2
黄金代换式
万有引力定律的应用
测天体的质量、密度
行星、卫星的运动
宇宙速度
同步卫星
思路一:天体表面重力近似等于万有引力
思路二:天体运动中,万有引力提供物体圆周运动向心力
重力加速度g
自我检测区
1
2
3
1.(天体质量的计算)“嫦娥三号”探月卫星于2013年12月2日凌晨在西昌卫星发射中心发射,实现了“落月”的新阶段.若已知引力常量为G,月球绕地球做圆周运动的半径为r1、周期为T1,“嫦娥三号”探月卫星做圆周运动的环月轨道半径为r2、周期为T2,不计其他天体的影响,根据题目条件可以( )
A.求出“嫦娥三号”探月卫星的质量
B.求出月球的质量
C.得出
D.求出地球的密度
1
2
3
两个模型:
月
月
可求中心天体质量
同
理
周期定律表达形式
条件:中心天体相同
1.(天体质量的计算)“嫦娥三号”探月卫星于2013年12月2日凌晨在西昌卫星发射中心发射,实现了“落月”的新阶段.若已知引力常量为G,月球绕地球做圆周运动的半径为r1、周期为T1,“嫦娥三号”探月卫星做圆周运动的环月轨道半径为r2、周期为T2,不计其他天体的影响,根据题目条件可以( )
A.求出“嫦娥三号”探月卫星的质量
B.求出月球的质量
C.得出
D.求出地球的密度
两个模型:
B
月
可求中心天体质量
周期定律表达形式
条件:中心天体相同
1
2
3
